2017多校训练Contest4: 1007 Matching In Multiplication hdu6073

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.



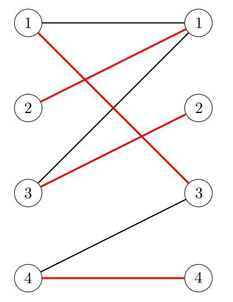
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

 

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

 

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

 

Sample Input

122 1 1 41 4 2 3

 

Sample Output

16

因为题目保证了至少存在一个完美匹配，且左边每个点度数为2，因此这张图一定是若干个不相交的环加上一些和环链接的链组成

我们首先tarjan缩点，把所有的环找出来，然后对于那些单点，我们只能选取不与环相连的那条变

然后对于每个环的每条边黑白染色，每个环的贡献就是黑边+白边

最后把所有的部分乘起来就可以了

#include<map>#include<cmath>#include<queue>#include<vector>#include<cstdio>#include<string>#include<cstring>#include<cassert>#include<iostream>#include<algorithm>using namespace std;long long mod=998244353;struct line{    int s,t;    long long x;    int next;}a[1200001];int head[600001];int edge;inline void add(int s,int t,int x){    a[edge].next=head[s];    head[s]=edge;    a[edge].s=s;    a[edge].t=t;    a[edge].x=x;}long long s1,s2;int n;bool v[600001];int scc,cnt;int s[600001],top;int dfn[600001],low[600001],belong[600001];int indeg[600001],outdeg[600001],siz[600001];void tarjan(int d,int fa){     int i,x;     cnt++;     dfn[d]=cnt;     low[d]=cnt;     top++;     s[top]=d;     v[d]=true;     for(i=head[d];i!=0;i=a[i].next)     {           x=a[i].t;//无向图记录fa[d],x==fa[d] continue           if(x==fa)               continue;          if(dfn[x]==0)           {               tarjan(x,d);               low[d]=min(low[d],low[x]);          }          else if(v[x]&&low[d]>dfn[x])//v在栈中，修改low[u]               low[d]=dfn[x];     }     if(dfn[d]==low[d])//u为该强连通分量中遍历所成树的根     {          scc++;          x=s[top];          siz[scc]=0;          top--;          while(x!=d)          {                   v[x]=false;               belong[x]=scc;               x=s[top];               siz[scc]++;               top--;          }          v[x]=false;          belong[x]=scc;          siz[scc]++;     }}int tot;struct circle{    long long x,y;}cir[300001];inline void dfs(int d,int col,int tt,int dd){    v[d]=true;    int i;    for(i=head[d];i!=0;i=a[i].next)    {        int t=a[i].t;        if(!v[t]&&belong[t]==col)        {            if(tt%2==0)                s1=s1*a[i].x%mod;            else                s2=s2*a[i].x%mod;            dfs(t,col,1-tt,dd);            return ;        }        else if(t==dd)        {            if(tt%2==0)                s1=s1*a[i].x%mod;            else                s2=s2*a[i].x%mod;            return ;        }    }}inline void dfsx(int d){    v[d]=true;    int i;    for(i=head[d];i!=0;i=a[i].next)    {        int t=a[i].t;        if(!v[t])        {            if(d<=n)                s1=s1*a[i].x%mod;            dfsx(t);        }    }}inline void circle_count(){    memset(v,false,sizeof(v));    int i,j;    tot=0;    for(i=1;i<=n;i++)    {        if(!v[i]&&siz[belong[i]]!=1)        {            s1=1;            s2=1;            dfs(i,belong[i],0,i);            tot++;            cir[tot].x=s1;            cir[tot].y=s2;        }    }    s1=1;    for(i=1;i<=n;i++)    {        int flag=0;        for(j=head[i];j!=0;j=a[j].next)        {            int t=a[j].t;            if(v[t])                flag++;        }        if(flag==1)        {            for(j=head[i];j!=0;j=a[j].next)            {                int t=a[j].t;                if(!v[t])                {                    s1=s1*a[j].x%mod;                    v[i]=true;                    dfsx(t);                    break;                }            }        }    }                    tot++;    cir[tot].x=s1;    cir[tot].y=0;}int main(){    int T;    scanf("%d",&T);    while(T>0)    {        edge=0;        memset(head,0,sizeof(head));        T--;        scanf("%d",&n);        int i;        int s,x;        for(i=1;i<=n;i++)        {            scanf("%d%d",&s,&x);            edge++;            add(i,s+n,x);            edge++;            add(s+n,i,x);            scanf("%d%d",&s,&x);            edge++;            add(i,s+n,x);            edge++;            add(s+n,i,x);        }        tot=0;        top=0;        cnt=0;        scc=0;        memset(dfn,0,sizeof(dfn));        memset(low,0,sizeof(low));        memset(v,false,sizeof(v));        for(i=1;i<=n;i++)            if(!dfn[i])                tarjan(i,0);        circle_count();        long long ans=1;        for(i=1;i<=tot;i++)            ans=ans*((cir[i].x+cir[i].y)%mod)%mod;        printf("%lld\n",ans);    }    return 0;}

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.



Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

 

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

 

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

 

Sample Input

122 1 1 41 4 2 3

 

Sample Output

16