LeetCode 4. Median of Two Sorted Arrays

[Chinese ver]

4. Median of Two Sorted Arrays

这里有两个有序数组nums1和nums2，他们各自的大小为m和n.
找到这两个数组的中间值，总的时间复杂度应该为O(log (m+n)).

Example 1:nums1 = [1, 3]nums2 = [2] 中间值是 2.0

Example 2:nums1 = [1, 2]nums2 = [3, 4]中间值是 (2 + 3)/2 = 2.5

• 4. Median of Two Sorted Arrays
  
  • 方法一：
  • 方法二：
  • 方法三：
  • 方法四：

方法一：

首先尝试了一种比较笨的方法

public class Solution {    public double findMedianSortedArrays(int[] nums1, int[] nums2) {        //需要几个数值        int needNum = 0;        //数值位置        int needIndex = 0;        //中间值        double median = 0;        int big = 0;        int stand = 0;        //合成的数组        int[] insertnum ;        int m = nums1.length;        int n = nums2.length;        if((m+n)%2==0){            needNum = 2;            needIndex = (m+n)/2-1;        }else{            needNum=1;            needIndex = (m+n)/2;        }        insertnum = new int[m+n];        //nums1的下标        int j =0;        //nums2的下标        int k = 0;        for(int i =0;i<m+n;i++){            if(k==n){                insertnum[i] = nums1[j];                j++;            }            else if(j==m){                insertnum[i] = nums2[k];                k++;            }else if(nums1[j]>nums2[k]){                insertnum[i] = nums2[k];                k++;            }else{                insertnum[i] = nums1[j];                j++;            }        }        if(needNum == 1){            median = Double.valueOf(insertnum[needIndex]);        }else{            median = Double.valueOf(insertnum[needIndex]+insertnum[needIndex+1]) /2.0;        }        return median;    }}

顺便提一下，这个方法经常无法通过，应该是时间复杂度过高的原因吧。

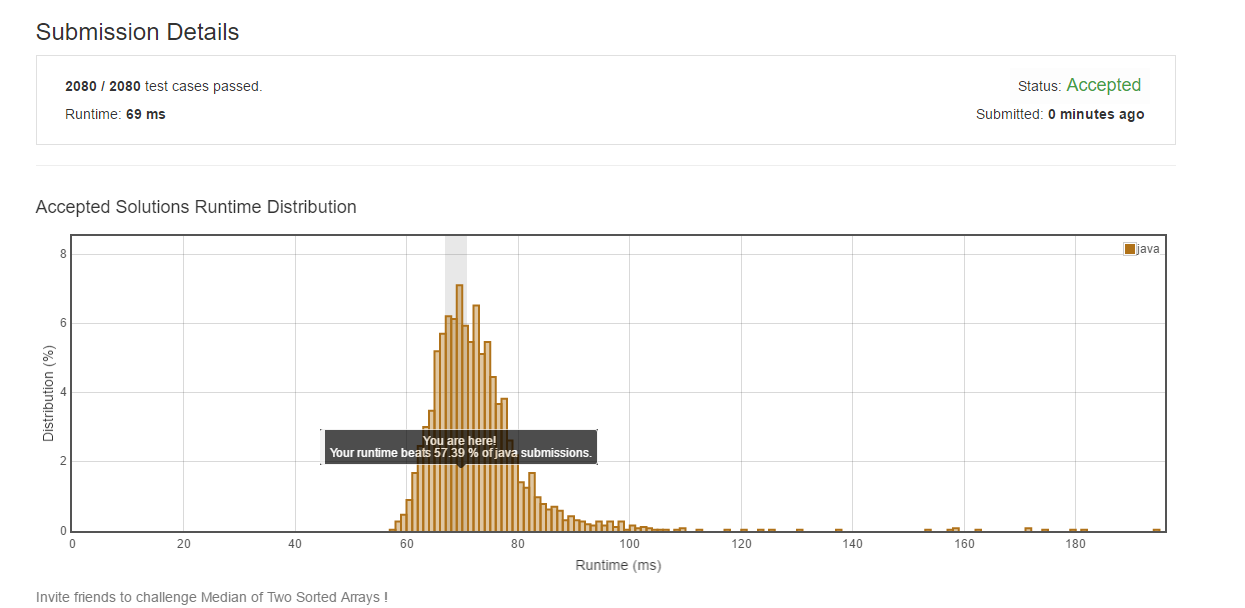
分析
这个方法的原理很简单，首先将两个数组个数和是奇数和偶数的情况所需的取值个数以及中间值计算方法得出。然后将两个数组按照从小到大的顺序合并成一个数组，最后根据前面得到的中间数的计算方法得出中间值。
时间复杂度 ： O(m+n) 。
空间复杂度 ： O(m+n) .

这个方法可以在做一个优化，如下：

public class Solution {    public double findMedianSortedArrays(int[] nums1, int[] nums2) {        int needNum = 0;        int needIndex = 0;        double median = 0;        int big = 0;        int stand = 0;        int[] insertnum ;        int m = nums1.length;        int n = nums2.length;        if((m+n)%2==0){            needNum = 2;            needIndex = (m+n)/2-1;        }else{            needNum=1;            needIndex = (m+n)/2;        }        insertnum = new int[(m+n)/2+1];        int j =0;        int k = 0;        for(int i =0;i<m+n;i++){            if(k==n){                insertnum[i] = nums1[j];                j++;            }            else if(j==m){                insertnum[i] = nums2[k];                k++;            }else if(nums1[j]>nums2[k]){                insertnum[i] = nums2[k];                k++;            }else{                insertnum[i] = nums1[j];                j++;            }             if (i >= needIndex ){                if (needNum == 1){                    median = Double.valueOf(insertnum[needIndex]);                    return median;                }else{                     if (i == needIndex+1){                         median = Double.valueOf(insertnum[needIndex]+insertnum[needIndex+1]) /2.0;                         return median;                     }                }            }        }    return median;    }}

分析
这个方法优化的地方就是通过事先得到中间值的位置，在得到该位置的数值之后就不继续往下走了。

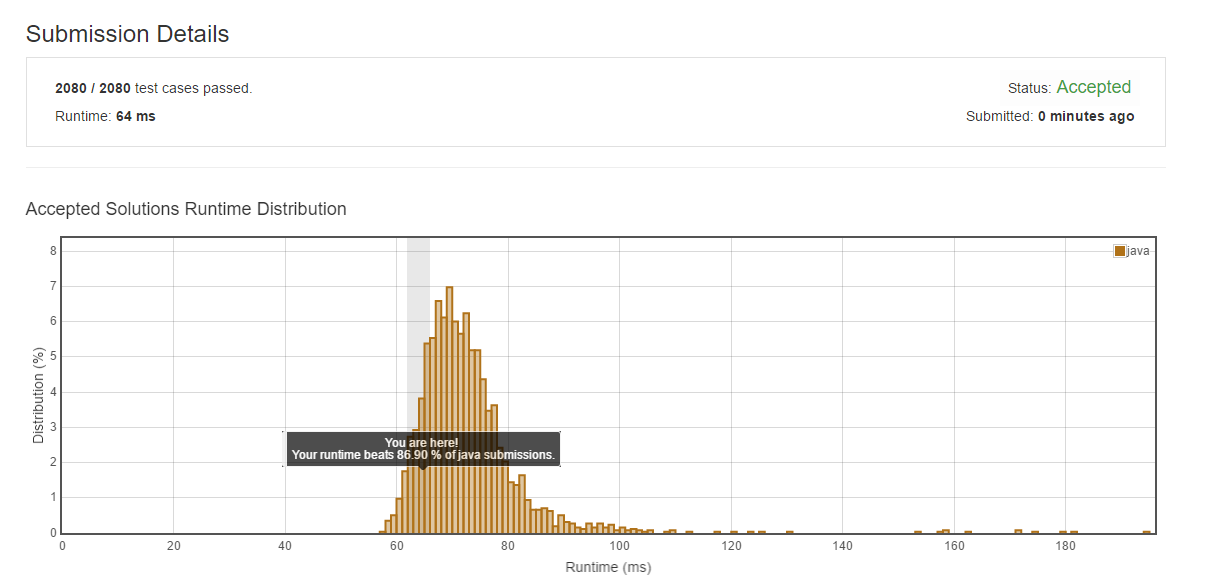
方法二：

public class Solution {       public double findMedianSortedArrays(int[] nums1, int[] nums2) {           int N1 = nums1.length;           int N2 = nums2.length;           if (N1 < N2)               return findMedianSortedArrays(nums2, nums1);    // Make sure A2 is the shorter one.           if (N2 == 0)               return ((double) nums1[(N1 - 1) / 2] + (double) nums1[N1 / 2]) / 2;  // If A2 is empty           int lo = 0, hi = N2 * 2;           while (lo <= hi) {               int mid2 = (lo + hi) / 2;   // Try Cut 2               int mid1 = N1 + N2 - mid2;  // Calculate Cut 1 accordingly               double L1 = (mid1 == 0) ? Integer.MIN_VALUE : nums1[(mid1 - 1) / 2];    // Get L1, R1, L2, R2 respectively               double L2 = (mid2 == 0) ? Integer.MIN_VALUE : nums2[(mid2 - 1) / 2];               double R1 = (mid1 == N1 * 2) ? Integer.MAX_VALUE : nums1[(mid1) / 2];               double R2 = (mid2 == N2 * 2) ? Integer.MAX_VALUE : nums2[(mid2) / 2];               if (L1 > R2)                   lo = mid2 + 1;        // A1's lower half is too big; need to move C1 left (C2 right)               else if (L2 > R1)                   hi = mid2 - 1;    // A2's lower half too big; need to move C2 left.               else                   return ((L1 > L2 ? L1 : L2) + (R1 > R2 ? R2 : R1)) / 2;    // Otherwise, that's the right cut.           }           return -1;       }   }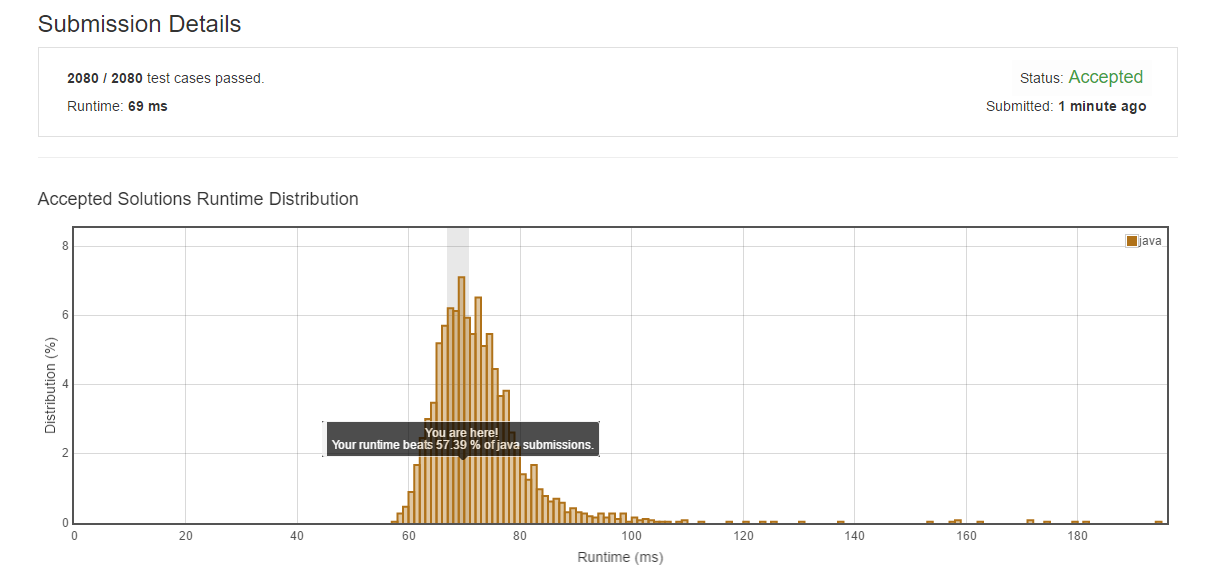

分析

这个问题比较困难，很多方法都是把他分成两种情况，奇数个和偶数个。实际上这样有点复杂，我们可以把这两个情况合并成一种情况。

首先，我们来重新定义一下’median’的含义：

“如果我们把一个有序的array分成两个等长的部分，那么median就是比较小的那一部分的最大值和比较大的那一部分的最小值的平均值。即划分线两边的数。”

比如[1,2],我们的分割线就应该在1，2之间，[1 | 2],结果是(1 + 2)/2.0 = 1.5。
同理，如果是两个有序的数组，那么我们只需要保证两个数组划分线右侧的数都大于左侧的数，并且两个数组左侧数字个数的和等于右侧数字个数的和。

我们使用‘|’来代表分割线，(n|n)来表示分割线正好在某个数字n上。
比如[1 2 3],得到的分割后的数组像这样[1 (2|2) 3],z中间值就是(2+2)/2.0 = 2

我们使用L代表分割线左边的数，R代表分割线右边的数。

可以观察到左边的数和右边的数有这样的规律。

N Index of L / R
1 0 / 0
2 0 / 1
3 1 / 1
4 1 / 2
5 2 / 2
6 2 / 3
7 3 / 3
8 3 / 4

可以得到 L = (N-1)/2, R = N/2. 中间值为(L + R)/2 = (A[(N-1)/2] + A[N/2])/2

为了更方便的计算两个数组的情况，我们添加一些空位在数字之间。用’#’代表，用’position’来表示增加空格后的位置信息。

[1 2] -> [# 1 # 2 #] (N=2)
position 0 1 2 3 4 (N_Position = 5)

[3 4] -> [# 3 # 4 #] (N=2)
position 0 1 2 3 4 (N_Position = 5)

可以看出N_Position = 2N+1.所以分割线是在N，index(L) = (CutPosition-1)/2, index(R) = (CutPosition)/2.

当我们分割这两个数组的时候要注意，总共有2N1+2N2+2的位置，所以，分割线的每一边都要有N1+N2个位置，剩下的2个就是切线的位置，所以当我们A2分割线在 C2 = K , 那么A1的分割线就必须要在C1 = N1 + N2 - k. 比如, C2 = 2, 那么 C1 = 2 + 2 - C2 = 2.

[# 1 | 2 #]
[# 3 | 4 #]
现在我们有了两个L和两个R。
L1 = A1[(C1-1)/2]; R1 = A1[C1/2];
L2 = A2[(C2-1)/2]; R2 = A2[C2/2];
即
L1 = A1[(2-1)/2] = A1[0] = 1; R1 = A1[2/2] = A1[1] = 2;
L2 = A2[(2-1)/2] = A2[0] = 3; R2 = A1[2/2] = A1[1] = 4;

那么我们要怎么判断这个分割线是不是符合规则的呢？我们只要左边的数字都小于右边的数字。首先这两个数组都是有序的，所以L1,L2是左半边数组里最大的数，R1,R2是右半边数组里最小的数，L1<=R1.L2<=R2.
所以我们只要判断L1<=R2,L2<=R1就可以了。

现在我们用简单的二分法查找就可以得到答案了。

如果L1>R2,代表A1左边有过多较大的数字，我们必须把C1往左移，同时需要把C2往右移。
如果L2>R1,代表A2左边有过多较大的数字，我们必须把C2往左移，同时需要把C1往右移。
反之则相反。

当我们找到正确的分割线位置的时候，中间值 = (max(L1, L2) + min(R1, R2)) / 2。

1.因为C1和C2可以根据彼此的值互相推断，我们可以使用较短的数组(设为A2)并且只移动C2，然后计算出C1。这样我们的时间复杂度就是O(log(min(N1, N2)))

2.只有在极限的条件下分割线会在0,或者2N的index。比如，C2=2N2,R2 = A2[2*N2/2] = A2[N2].这种情况下他有一边是没有数值的，我们可以把它当成是极大或者极小，L = INT_MIN ，R = INT_MAX.

时间复杂度 ： O(log(min(m,n))) 。m,n是两个数组的长度。
空间复杂度 ： O(1) .

方法三：

public class Solution {  public double findMedianSortedArrays(int A[], int B[]) {       int n = A.length;       int m = B.length;       // the following call is to make sure len(A) <= len(B).       // yes, it calls itself, but at most once, shouldn't be       // consider a recursive solution       if (n > m)           return findMedianSortedArrays(B, A);       // now, do binary search       int k = (n + m - 1) / 2;       int l = 0, r = Math.min(k, n); // r is n, NOT n-1, this is important!!       while (l < r) {           int midA = (l + r) / 2;           int midB = k - midA;           if (A[midA] < B[midB])               l = midA + 1;           else               r = midA;       }       // after binary search, we almost get the median because it must be between       // these 4 numbers: A[l-1], A[l], B[k-l], and B[k-l+1]       // if (n+m) is odd, the median is the larger one between A[l-1] and B[k-l].       // and there are some corner cases we need to take care of.       int a = Math.max(l > 0 ? A[l - 1] : Integer.MIN_VALUE, k - l >= 0 ? B[k - l] : Integer.MIN_VALUE);       if (((n + m) & 1) == 1)           return (double) a;       // if (n+m) is even, the median can be calculated by       //      median = (max(A[l-1], B[k-l]) + min(A[l], B[k-l+1]) / 2.0       // also, there are some corner cases to take care of.       int b = Math.min(l < n ? A[l] : Integer.MAX_VALUE, k - l + 1 < m ? B[k - l + 1] : Integer.MAX_VALUE);       return (a + b) / 2.0;   }}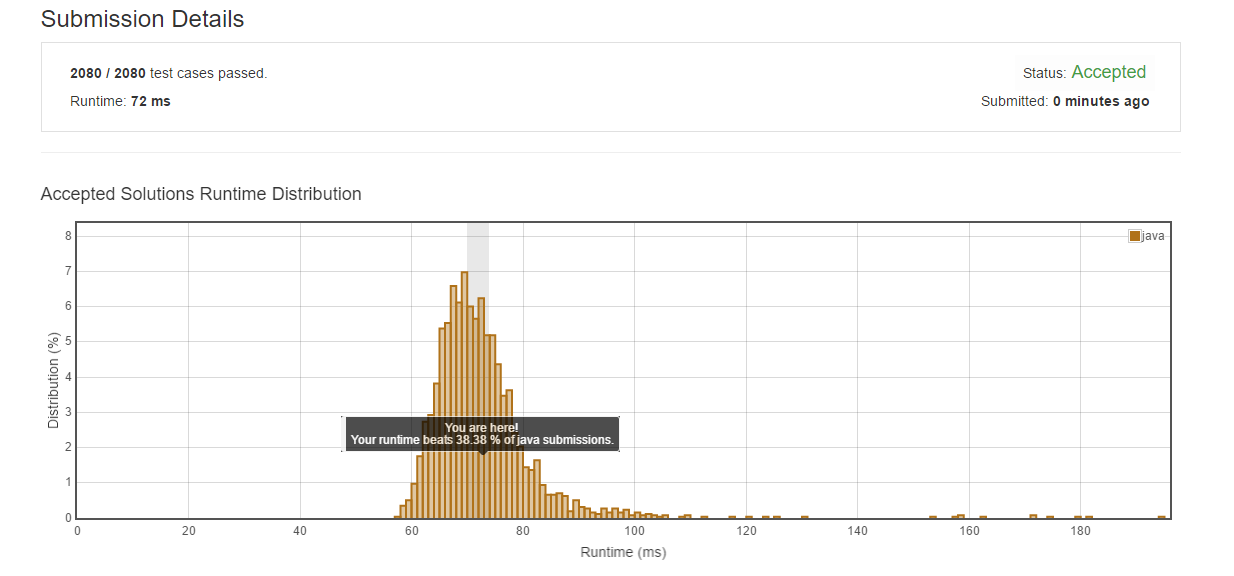

分析
这个方法的原理和上一个方法是大致相同的。
时间复杂度 ： O(log(min(m,n))) 。m,n是两个数组的长度。
空间复杂度 ： O(1) .

方法四：

public class Solution {  public double findMedianSortedArrays(int[] A, int[] B) {              int m = A.length, n = B.length;              int l = (m + n + 1) / 2;//position of l element (not the index)              int r = (m + n + 2) / 2;//position of r element (not the index)              return (getkth(A, 0, B, 0, l) + getkth(A, 0, B, 0, r)) / 2.0;          }  public double getkth(int[] A, int aStart, int[] B, int bStart, int k) {          //when the start position is bigger than A.length -1 ,means the median doesn't in the A.          if (aStart > A.length - 1) return B[bStart + k - 1];          if (bStart > B.length - 1) return A[aStart + k - 1];          if (k == 1) return Math.min(A[aStart], B[bStart]);          int aMid = Integer.MAX_VALUE, bMid = Integer.MAX_VALUE;          if (aStart + k/2 - 1 < A.length) aMid = A[aStart + k/2 - 1];          if (bStart + k/2 - 1 < B.length) bMid = B[bStart + k/2 - 1];          if (aMid < bMid)              return getkth(A, aStart + k/2, B, bStart, k - k/2);// Check: aRight + bLeft          else              return getkth(A, aStart, B, bStart + k/2, k - k/2);// Check: bRight + aLeft  }}

分析
这个方法的原理是这样的，从两个数组中间值开始通过递归对比，每次排除一半的选项。如果A的中间值小于B的中间值则保留a的右侧数字和b的左侧数字。反之相反。然后得到l和r位置的数字,再相加除以2即可。需要注意的是这里的l和r不是index，不是从零开始的。如果两个数组的长度的和是奇数的话l和r是相同的，偶数则不同。
时间复杂度 ： O(log(m + n))
空间复杂度 ： O(1)

如果你有更好的办法或者对我这里的描述有其他看法，请联系我。谢谢