几种关于卷积的深刻而有趣的理解【看过绝对不会再忘了】
来源:互联网 发布:mac用pe安装win7系统 编辑:程序博客网 时间:2024/06/05 15:38
注明:有些图片可能看不到,请查看原网页。
(一)
链接:https://www.zhihu.com/question/21686447/answer/50481954
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
对于初学者,我推荐用复利的例子来理解卷积可能更直观一些:
小明存入100元钱,年利率是5%,按复利计算(即将每一年所获利息加入本金,以计算下一年的利息),那么在五年之后他能拿到的钱数是<img src="https://pic2.zhimg.com/50/5fa86c80c31dd277d038527555aa4d75_hd.jpg" data-rawwidth="1293" data-rawheight="95" class="origin_image zh-lightbox-thumb" width="1293" data-original="https://pic2.zhimg.com/5fa86c80c31dd277d038527555aa4d75_r.jpg">将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是
 将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是
将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是<img src="https://pic4.zhimg.com/50/39f37df8c96d7219cba5d081919a3a2f_hd.jpg" data-rawwidth="1296" data-rawheight="134" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic4.zhimg.com/39f37df8c96d7219cba5d081919a3a2f_r.jpg">以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:
 以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:
以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:<img src="https://pic2.zhimg.com/50/cfe98b9d33640fae02a21bf369f0459d_hd.jpg" data-rawwidth="1296" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_r.jpg">可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:
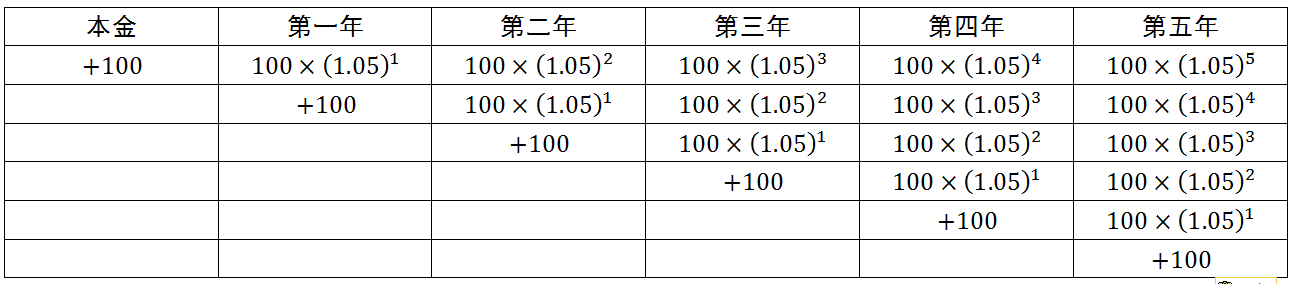 可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:
可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:<img src="https://pic3.zhimg.com/50/fba65159d3472936979002b01b606a0e_hd.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg">用求和符号来简化这个公式,可以得到:

用求和符号来简化这个公式,可以得到:
在上式中,为小明的存钱函数,而
为存入银行的每一笔钱的复利计算函数。在这里,小明最终得到的钱就是他的存钱函数和复利计算函数的卷积。
为了更清晰地看到这一点,我们将这个公式推广到连续的情况,也就是说,小明在从到
的这一段时间内,每时每刻都往银行里存钱,他的存钱函数为
,而银行也对他存入的每一笔钱按复利公式计算收益:
,则小明到时间
将得到的总钱数为:
这也就是卷积的表达式了,上式可以记为。
相信通过上面这个例子,大家应该能够很清晰地记住卷积公式了。下面我们再展开说两句:
如果我们将小明的存款函数视为一个信号发生(也就是激励)的过程,而将复利函数(二)
链接:https://www.zhihu.com/question/21686447/answer/26614025
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
比如说你的老板命令你干活,你却到楼下打台球去了,后来被老板发现,他非常气愤,扇了你一巴掌(注意,这就是输入信号,脉冲),于是你的脸上会渐渐地(贱贱地)鼓起来一个包,你的脸就是一个系统,而鼓起来的包就是你的脸对巴掌的响应,好,这样就和信号系统建立起来意义对应的联系。下面还需要一些假设来保证论证的严谨:假定你的脸是线性时不变系统,也就是说,无论什么时候老板打你一巴掌,打在你脸的同一位置(这似乎要求你的脸足够光滑,如果你说你长了很多青春痘,甚至整个脸皮处处连续处处不可导,那难度太大了,我就无话可说了哈哈),你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包来,并且假定以鼓起来的包的大小作为系统输出。好了,那么,下面可以进入核心内容——卷积了!
如果你每天都到地下去打台球,那么老板每天都要扇你一巴掌,不过当老板打你一巴掌后,你5分钟就消肿了,所以时间长了,你甚至就适应这种生活了……如果有一天,老板忍无可忍,以0.5秒的间隔开始不间断的扇你的过程,这样问题就来了,第一次扇你鼓起来的包还没消肿,第二个巴掌就来了,你脸上的包就可能鼓起来两倍高,老板不断扇你,脉冲不断作用在你脸上,效果不断叠加了,这样这些效果就可以求和了,结果就是你脸上的包的高度随时间变化的一个函数了(注意理解);如果老板再狠一点,频率越来越高,以至于你都辨别不清时间间隔了,那么,求和就变成积分了。可以这样理解,在这个过程中的某一固定的时刻,你的脸上的包的鼓起程度和什么有关呢?和之前每次打你都有关!但是各次的贡献是不一样的,越早打的巴掌,贡献越小,所以这就是说,某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出,然后再把不同时刻的输出点放在一起,形成一个函数,这就是卷积,卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消肿,可是如果连续打,几个小时也消不了肿了,这难道不是一种平滑过程么?反映到剑桥大学的公式上,f(a)就是第a个巴掌,g(x-a)就是第a个巴掌在x时刻的作用程度,乘起来再叠加就ok了,大家说是不是这个道理呢?我想这个例子已经非常形象了,你对卷积有了更加具体深刻的了解了吗?
(三)
链接:https://www.zhihu.com/question/21686447/answer/22430109
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
有一个挺有意思的例子,我以前在万门大学童哲校长的公开课上看到的:
我们在研究一个人一天24小时肚子里还剩多少东西,记为函数我们有如下信息:
- 此人吃下去的东西在肚里按指数衰减,即如果他肚子里现在有食物量 1,剩余量按消化时间的变化便是
,其中
为衰减常数;
- 此人今天吃饭的量是:在早上7点、中午12点和晚上18点各进餐
,并假设在其他时间没有吃东西。要写作函数的话,应该是
,其中
是Dirac脉冲函数。如果不熟悉的话,可以认为此人在饭点儿瞬间往肚子里塞那么多食物。
<img src="https://pic3.zhimg.com/50/04e88a749fefb7de7cb73fdbb49748d2_hd.jpg" data-rawwidth="560" data-rawheight="189" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic3.zhimg.com/04e88a749fefb7de7cb73fdbb49748d2_r.jpg">图:“消化规律”
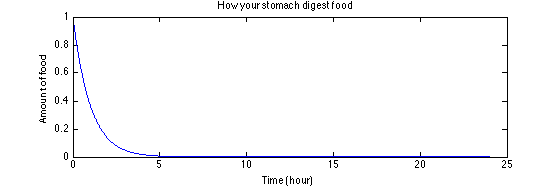 图:“消化规律”
图:“消化规律”可以看到:大概五个小时肚子里的东西就差不多消化完了。
<img src="https://pic1.zhimg.com/50/2fc04d83d0cf2056333cf986e678182c_hd.jpg" data-rawwidth="560" data-rawheight="199" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic1.zhimg.com/2fc04d83d0cf2056333cf986e678182c_r.jpg">
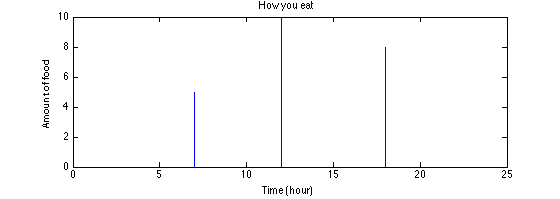
图:“今儿的吃法”
好了,我们现在看考察一下,比如说下午15点,这人肚子里还剩多少东西:- 早饭吃的
,经过15-7 =8小时的消化(按指数衰减),还剩
;
- 中饭吃的
,经过15-12 = 3小时的消化,还剩
;
- 晚饭还没吃呢,自然不算。
加起来就是:
考察任意时间,就有卷积
你可以仔细看一下,上面t=15的情况可以从这个式子里面导出[注1]。
也请看图:
<img src="https://pic3.zhimg.com/50/4458a2fc87c80d42759b1031453ca6b2_hd.jpg" data-rawwidth="560" data-rawheight="420" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic3.zhimg.com/4458a2fc87c80d42759b1031453ca6b2_r.jpg">图:(上)吃法儿; (下)肚里食物量
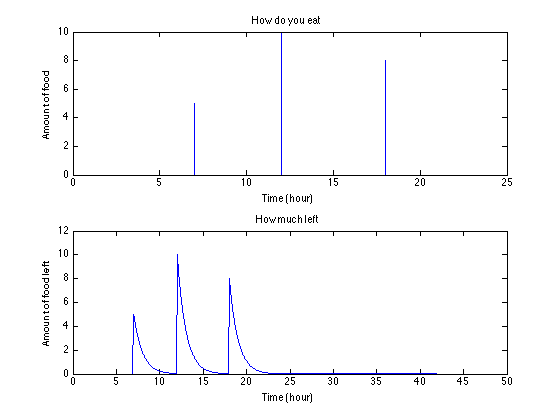
图:(上)吃法儿; (下)肚里食物量
其实在前面的讨论里面,我们把“吃饭的量”看作输入,“肚子里还剩的食物”看作输出。并且我们假设:
- 消化系统是线性的,即:如果(1)按吃法
产生肚子里食物量变化
;并且(2)按吃法
产生肚子里食物量变化
,那么对任意常数a,b,按吃法
会产生肚子里食物量变化
.
- 消化系统是时不变的,即:对任意时间间隔
,若按吃法
产生肚子里食物量变化
,则按吃法
将产生肚子里食物量变化
.
在这样线性时不变(Linear and Time-Invariant, LTI)系统里,上面的函数:
- 此人肚子的”消化规律“
是系统的冲激响应;
- 此人今天”吃饭的量“
是激励(输入);
- 我们考察的肚子里”还剩的食物量“
是响应(输出)。
任何一个线性时不变系统都可以由冲激响应完全描述。
它的输入输出关系正是卷积:
/*-----------------------------------------------------------*/
上面有几个参数可以变化,我们来玩一玩:
比如说:这兄弟最近消化不大好,也就是冲激响应里面的衰减系数<img src="https://pic4.zhimg.com/50/ceea93a21c3f62231adbab4ad610ca17_hd.jpg" data-rawwidth="560" data-rawheight="420" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic4.zhimg.com/ceea93a21c3f62231adbab4ad610ca17_r.jpg">(最近消化不大好)上:吃法儿; 下:肚里食物量
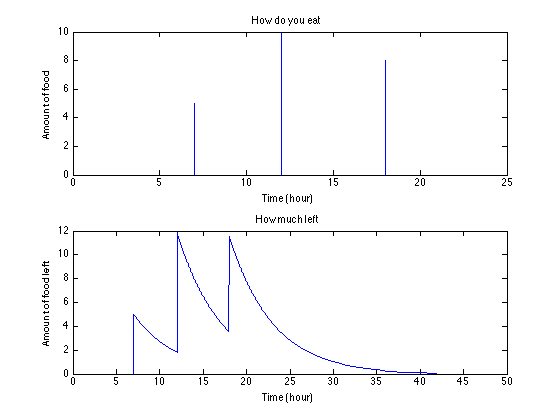
(最近消化不大好)上:吃法儿; 下:肚里食物量
你可以看到前一顿儿还没消化完,就到吃下一顿了。如果按原计划吃,实在要把肚子撑坏。。(峰值大概12,比上面的结果大了很多)
<img src="https://pic3.zhimg.com/50/66a949d261953f9a2f87504e590d352e_hd.jpg" data-rawwidth="560" data-rawheight="420" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic3.zhimg.com/66a949d261953f9a2f87504e590d352e_r.jpg">
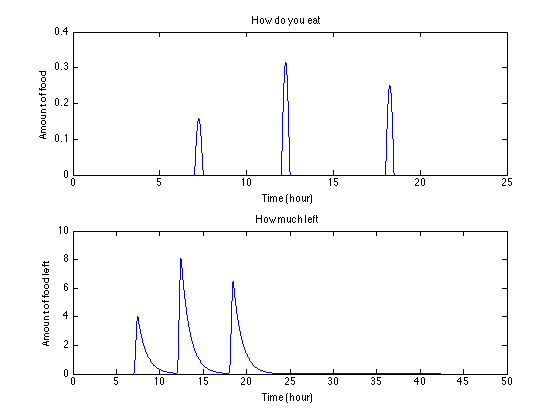
(花半小时吃饭,而且在正常消化状态)上:吃法儿; 下:肚里食物量
你可以看到,峰值(大概8)进一步减小了,细嚼慢咽就是好。
<img src="https://pic1.zhimg.com/50/1f032f2f219ba395e15cdfda36dba94c_hd.jpg" data-rawwidth="560" data-rawheight="420" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic1.zhimg.com/1f032f2f219ba395e15cdfda36dba94c_r.jpg">(花一个小时吃饭,而且在正常消化状态)上:吃法儿; 下:肚里食物量
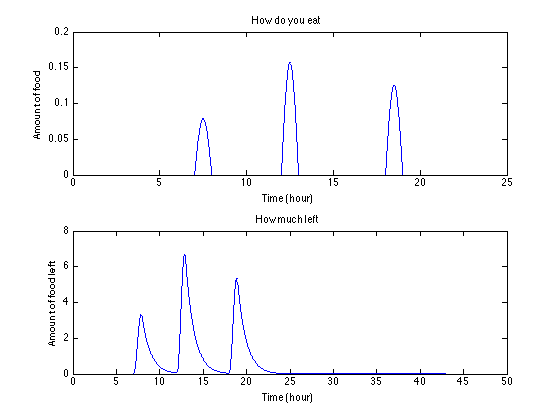
(花一个小时吃饭,而且在正常消化状态)上:吃法儿; 下:肚里食物量
嗯,对肚子压力更小一点了。
<img src="https://pic1.zhimg.com/50/e776e04bbc562024987a1006abf2fadc_hd.jpg" data-rawwidth="560" data-rawheight="420" class="origin_image zh-lightbox-thumb" width="560" data-original="https://pic1.zhimg.com/e776e04bbc562024987a1006abf2fadc_r.jpg">(过年的时候,每顿花三个小时,吃得多而且肠胃状态不那么好)上:吃法儿; 下:肚里食物量
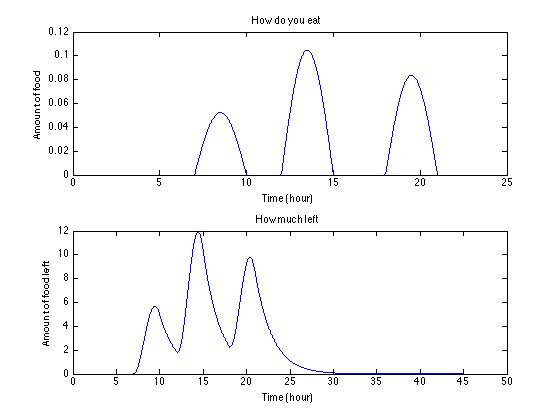
(过年的时候,每顿花三个小时,吃得多而且肠胃状态不那么好)上:吃法儿; 下:肚里食物量
可以看到,这个峰值和最前面那种瞬间吃好饭的状况差不多了,而且过了半夜还没消化完。
所以,不要暴饮暴食噢!
最后这一部分有点娱乐性质,主要是画图的时候玩儿上了。。哈哈
并且用线性时不变的模型来模拟人吃饭消化,可能有不妥,比如:人的胃不是线性的,因为有总容量的限制,而且估计也不是时不变,因为吃的太多时肚子消化能力大概会变弱。拿这个仅仅用于举例子咯。
希望有帮到你。也请各位朋友赐教!
/*-----------------------------------------------------------*/
[注1]t=15的情况:
激励(输入)
冲击响应(系统)
求响应(输出)
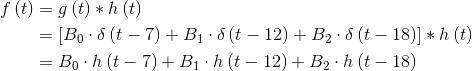 这里用到:
这里用到:<img src="https://pic4.zhimg.com/50/ece42d9ca0280295259f582e86469d4f_hd.png" data-rawwidth="195" data-rawheight="18" class="content_image" width="195">
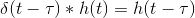
当
<img src="https://pic4.zhimg.com/50/640dcbf2b52db40770a1b9764567bbdf_hd.jpg" data-rawwidth="338" data-rawheight="71" class="content_image" width="338">注意:
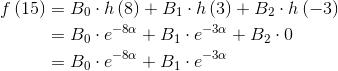 注意:<img src="https://pic3.zhimg.com/50/9f0c9a82feccc3cadd6c84b250aa4f3a_hd.jpg" data-rawwidth="124" data-rawheight="18" class="content_image" width="124">
注意:<img src="https://pic3.zhimg.com/50/9f0c9a82feccc3cadd6c84b250aa4f3a_hd.jpg" data-rawwidth="124" data-rawheight="18" class="content_image" width="124">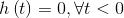
- 几种关于卷积的深刻而有趣的理解【看过绝对不会再忘了】
- 汉诺塔问题深刻而简单的理解
- 关于接口的深刻理解
- 关于卷积神经网络的几种结构
- 我看过的,印象深刻的网络小说
- 看过的印象深刻的电影
- 最近看过的几本给我印象深刻的书
- 关于卷积的一点理解
- 关于CNN的卷积理解
- 关于WM_ERASEBKGND和WM_PAINT的深刻理解
- 关于WM_ERASEBKGND和WM_PAINT的深刻理解
- 关于WM_ERASEBKGND和WM_PAINT的深刻理解
- 关于WM_ERASEBKGND和WM_PAINT的深刻理解
- 我绝对不会破坏现在的生活了
- 卷积的再理解
- 近期看过的有趣开源代码
- 句柄的深刻理解
- Layout_weight的深刻理解
- Hadoop学习第一天
- 计算机类中文核心期刊
- OpenCV Contrib Modules
- 写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和,例如,调用DigitSum(1729),则应该返回1+7+2+9,它的和是19
- 多线程的一些问题
- 几种关于卷积的深刻而有趣的理解【看过绝对不会再忘了】
- PAT Basic 1010
- 将一个字符串的前n个字符旋转到后面,采用左旋,或者右旋。
- ubuntu系统入门常用命令
- 使用 IDEA 的 Live Template 实现自动提示代码功能
- linux篇之安装jdk环境
- 从贝叶斯方法谈到贝叶斯网络
- Linux 中颜色显示
- Spring AOP详解


