Going Home

Going Home

Time Limit:1000MS  Memory Limit:65536K
Total Submit:19 Accepted:6

Description

On a grid map there are n little men and n houses. In each unit time, every little man can move one unit step, either horizontally, or vertically, to an adjacent point. For each little man, you need to pay a $1 travel fee for every step he moves, until he enters a house. The task is complicated with the restriction that each house can accommodate only one little man.

Your task is to compute the minimum amount of money you need to pay in order to send these n little men into those n different houses. The input is a map of the scenario, a '.' means an empty space, an 'H' represents a house on that point, and am 'm' indicates there is a little man on that point.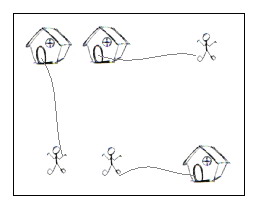

You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.

 

Input

There are one or more test cases in the input. Each case starts with a line giving two integers N and M, where N is the number of rows of the map, and M is the number of columns. The rest of the input will be N lines describing the map. You may assume both N and M are between 2 and 100, inclusive. There will be the same number of 'H's and 'm's on the map; and there will be at most 100 houses. Input will terminate with 0 0 for N and M.

Output

For each test case, output one line with the single integer, which is the minimum amount, in dollars, you need to pay.

Sample Input

2 2.mH.5 5HH..m...............mm..H7 8...H.......H.......H....mmmHmmmm...H.......H.......H....0 0

 

Sample Output

21028

 

Source

Pacific Northwest 2004

 

El’ÌEl

 

 

今天学习了最佳匹配，也就是二分图最大匹配。

先贴一些资料：

 

带权二分图：二分图的每条边（i,j)均带有一个权W（i,j)。一个匹配的权是匹配各边的和。

可行结点标号：是定义在V上的一个实数函数l， 满足条件：对于任意x属于X,y属于Y
    l(x)+l(y)大于或等于w(x,y)，l(v)称为结点v的标号。

等式子图:关于标号l的等式子图Gl=(V,El), El={(x,y):l(x)+l(y)=w(x,y)}

 

 

定理：设l是 G的可行标号，M是等式子图Gl的完美匹配，则M是G的最大权匹配。

设有可行标号l和El的一个匹配M
当M不是完美匹配时重复下列步骤：
在El中寻找M可增广道路，并扩展匹配；
El’,Ì如果可增广道路不存在，将l改进为l’使得El 转1。
注意到循环体总是增加M或者El的大小，故算法终止，而且此时M是El的完美匹配，因此是最大权匹配。

1.从一个初始标号l出发,求出El, 然后在其中任取匹配M; 利用Hungarian算法求 El的最大匹配.
2.如果找到了 El完美匹配，则此匹配是G的完美匹配。
3.否则，M的一个交互树H不包含可增广道路，不能继续扩展。修改标号l, 使得新标号的等式子图扩展了El, 并且包含了M和H, 然后继续扩展H。
4.重复3，直至找到等式子图的完美匹配。

其中涉及到几个概念，二分图，等式子图，匹配图。

二分图根据可行标等于权值得到等式了图，在等式了图上运用匈牙利算法寻找增广轨得到匹配图。

int km()

{

      int i;

      memset(math,-1,sizeof(math));

     for(i=0;i<n;i++)   //每次匹配一个

     {
   memset(visit,0,sizeof(visit));
   while(!dfs(i))
   {
    adjust(i);
    memset(visit,0,sizeof(visit));
   }

     }

}

 

 

KM算法是通过给每个顶点一个标号（叫做顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。设顶点Xi的顶标为A[i]，顶点Yi的顶标为B[i]，顶点Xi与Yj之间的边权为w[i,j]。在算法执行过程中的任一时刻，对于任一条边(i,j)，A[i]+B[j]>=w[i,j]始终成立。KM算法的正确性基于以下定理：

　　若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

　　这个定理是显然的。因为对于二分图的任意一个匹配，如果它包含于相等子图，那么它的边权和等于所有顶点的顶标和；如果它有的边不包含于相等子图，那么它的边权和小于所有顶点的顶标和。所以相等子图的完备匹配一定是二分图的最大权匹配。

　　初始时为了使A[i]+B[j]>=w[i,j]恒成立，令A[i]为所有与顶点Xi关联的边的最大权，B[j]=0。如果当前的相等子图没有完备匹配，就按下面的方法修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止。

　　我们求当前相等子图的完备匹配失败了，是因为对于某个X顶点，我们找不到一条从它出发的交错路。这时我们获得了一棵交错树，它的叶子结点全部是X顶点。现在我们把交错树中X顶点的顶标全都减小某个值d，Y顶点的顶标全都增加同一个值d，那么我们会发现：

两端都在交错树中的边(i,j)，A[i]+B[j]的值没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。

两端都不在交错树中的边(i,j)，A[i]和B[j]都没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。

X端不在交错树中，Y端在交错树中的边(i,j)，它的A[i]+B[j]的值有所增大。它原来不属于相等子图，现在仍不属于相等子图。

X端在交错树中，Y端不在交错树中的边(i,j)，它的A[i]+B[j]的值有所减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。

　　现在的问题就是求d值了。为了使A[i]+B[j]>=w[i,j]始终成立，且至少有一条边进入相等子图，d应该等于min{A[i]+B[j]-w[i,j]|Xi在交错树中，Yi不在交错树中}。

　　以上就是KM算法的基本思路。但是朴素的实现方法，时间复杂度为O(n4)——需要找O(n)次增广路，每次增广最多需要修改O(n)次顶标，每次修改顶标时由于要枚举边来求d值，复杂度为O(n2)。实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数slack，每次开始找增广路时初始化为无穷大。在寻找增广路的过程中，检查边(i,j)时，如果它不在相等子图中，则让slack[j]变成原值与A[i]+B[j]-w[i,j]的较小值。这样，在修改顶标时，取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点：修改顶标后，要把所有的slack值都减去d。

 

#include<stdio.h>#include<string>#include<cmath>int g[105][105];//邻接矩阵int m[105][2];//存储人所在位置的坐标int h[105][2];//存储房子所在位置的坐标int lx[105],ly[105];//顶点标号bool sx[105],sy[105];//是否在交错树中int link[105],n;char ss[105][105];#define INF 1<<25int min(int a,int b){if(a<b) return a;return b;}/*theory:若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。*/bool path(int k)//find augment path from x[k]{int i;sx[k]=true;for(i=0;i<n;i++){if(!sy[i]&&(lx[k]+ly[i]==g[k][i]))//if y[i] is not in the 交错树 and match the condition to be an edge in the 相等子图(after broaden condition){sy[i]=1;//give it a flag to be in the 交错树if(link[i]==-1||path(link[i])){link[i]=k;return true;}}}return false;}int BestMatch()//求解最小权匹配{int d,sum,i,j;memset(ly,0,sizeof(ly));memset(link,-1,sizeof(link));//初始时为了使A[i]+B[j]>=w[i,j]恒成立，令A[i]为所有与顶点Xi关联的边的最大权，B[j]=0。for(i=0;i<n;i++){lx[i]=-1; //x中顶点i的编号为与i关联的Y中边的最大权重for(j=0;j<n;j++)if(lx[i]<g[i][j])lx[i]=g[i][j];}for(int k=0;k<n;k++){while(1){memset(sx,0,sizeof(sx));memset(sy,0,sizeof(sy));if(path(k))break;//匹配成功//如果当前的相等子图没有完备匹配，就按下面的方法修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止。d=INF;//in order to make { lx[i]+ly[j]>=w[i,j] } all the way, and at least one edge be added into 相等子图,d 应该=min{lx[i]+ly[j]-w[i,j] |Xi在交错树中;Yi不在交错树中int i;for(i=0;i<n;i++)if(sx[i])for(int j=0;j<n;j++)if(!sy[j])d=min(d,lx[i]+ly[j]-g[i][j]);for(i=0;i<n;i++){if(sx[i]) lx[i]-=d;if(sy[i]) ly[i]+=d;}}}sum=0;for(i=0;i<n;i++) sum+=g[link[i]][i];//注意这里本来是求的最大权匹配,这里取反即为最小权匹配(因为临街矩阵中的边的权值也取反了)return -sum;}int main(){int mi,hi,M,N,ans,i,j;while(scanf("%d%d",&N,&M)!=EOF){if(N==0&&M==0) break;mi=hi=0;for(i=0;i<N;i++){scanf("%s",ss[i]);for(j=0;j<M;j++){if(ss[i][j]=='m'){m[mi][0]=i;m[mi][1]=j;mi++;}else if(ss[i][j]=='H'){h[hi][0]=i;h[hi][1]=j;hi++;}}}n=mi;for(i=0;i<n;i++)for(j=0;j<n;j++)g[i][j]=-(abs(m[i][0]-h[j][0])+abs(m[i][1]-h[j][1]));//即将边的权值取反printf("%d/n",BestMatch());}return 0;}

 

 

 

这道题还有一个正解：最小费用最大流！

构图如下：

 

 

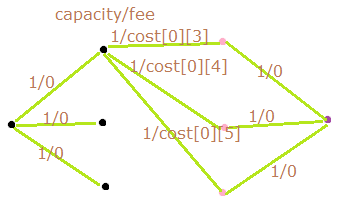
这个代码北大过了，不知道为啥NBU的很强大，过不了= =！

#include<iostream>#include<math.h>using namespace std;bool visited[205];int house[205][2];int man[205][2];char str[205];struct Node{int pre,flow,cost; }label[205];struct edge{int cap,currentflow;int unitcost;}network[205][205];void intial(int n) {for(int i = 0 ;i < n;i++)label[i].cost = 1000000000,label[i].flow = 0,label[i].pre = 0;}void Intial(int n) {for(int i = 0; i < n;i++)for(int j = 0; j < n;j++)network[i][j].cap = network[i][j].unitcost = network[i][j].currentflow = 0;}struct Vertix{int vertix,cost;Vertix(int v = 0,int c = 0):vertix(v),cost(c){} bool operator > (const Vertix& lhs) const{ return (lhs.cost<cost);}};bool modefiedDijkstra(int n,int s,int t){intial(n);fill_n(visited,n,false);Vertix w;w.cost = 0,w.vertix = s; label[s].pre = -1,label[s].flow = 1000000000,label[s].cost = 0;int v = 0,u = 0;while(true){ int minv = 10000000000;for(int w = 0; w < n;w++)if(!visited[w]&&label[w].cost < minv){v = w,minv = label[w].cost;}if(v == t)if(label[t].cost >= 1000000000)return false;elsereturn true; visited[v] = true;for(u = 0; u < n;u++)if(!visited[u]){ if(network[v][u].cap > 0&&network[v][u].cap - network[v][u].currentflow > 0&&label[v].cost + network[v][u].unitcost < label[u].cost){label[u].pre = v;label[u].cost = label[v].cost + network[v][u].unitcost;label[u].flow = min(label[v].flow,network[v][u].cap - network[v][u].currentflow); }else if(network[u][v].cap > 0&&network[u][v].currentflow > 0&&label[v].cost - network[u][v].unitcost < label[u].cost){ label[u].pre = v;label[u].flow = min(label[v].flow,network[u][v].currentflow);label[u].cost = label[v].cost - network[u][v].unitcost; }}}}void arguementpath(int t){for(int k = t;k != -1;k = label[k].pre){if(network[label[k].pre][k].cap > 0)network[label[k].pre][k].currentflow += label[t].flow;elsenetwork[k][label[k].pre].currentflow -= label[t].flow;}}void MaxFlowMincostAlgorithm(int n,int s,int t){int mincost = 0;while(modefiedDijkstra(n,s,t)){arguementpath(t); mincost += label[t].cost;}printf("%d/n",mincost);}void add(int x,int y,int cap,int cost){network[x][y].cap += cap;network[x][y].unitcost += cost;}int main(){int N,M,m,h,i,j;while ( scanf ( "%d%d", &N, &M ) && ( N || M ) ){m = 0,h = 0;for (i = 0; i < N; i++ ){scanf ( "%s", &str );for (j = 0; j < M; j++){if (str[j] == 'H'){house[h][0] = i;house[h][1] = j;h++;continue;}if (str[j] == 'm'){man[m][0] = i;man[m][1] = j;m++;continue;}}}Intial(m + h + 2);for (i = 0; i < m; i++)add (0,i + 1,1,0);for (i = 0; i < m; i++){for (j = 0; j < h; j++ ){int weight = abs(man[i][0]-house[j][0]) + abs(man[i][1]-house[j][1]);add (i + 1,m + j + 1,1,weight); }}for ( j = 0; j < h; j++ )add (m + j + 1, m + h + 1,1,0);MaxFlowMincostAlgorithm(m + h + 2,0,m + h + 1);//MaxFlowMincostAlgorithm(int n,int s,int t)}return 0;}  

 

下面这个都能过，当作模板

#include <iostream> #include<cmath>#include <queue> using namespace std; #define abs(x) (x<0?-x:x) #define MAXN 205 #define MIN(x,y) (x<y?x:y) #define INF 200005 int map[MAXN][MAXN],cost[MAXN][MAXN]; int pre[MAXN];//pre[i] record i's parentint max_flow[MAXN];//max_flow[i] record the max capacity can be added from s to i int flow[MAXN][MAXN];//current flowint dist[MAXN];//min cost from source to i record as dist[i]queue<int> my_queue; bool in_queue[MAXN]; bool SPFA(int num,int source,int sink) { memset(in_queue,0,sizeof(in_queue)); memset(pre,-1,sizeof(pre)); for(int i=0;i<num;i++) { dist[i]=INF; } dist[source]=0; my_queue.push(source); in_queue[source]=true; max_flow[source]=INF; while(!my_queue.empty()) { int temp=my_queue.front(); my_queue.pop(); for(int i=0;i<num;i++) { if((map[temp][i]-flow[temp][i]>0)&&(dist[temp]+cost[temp][i]<dist[i])) { dist[i]=dist[temp]+cost[temp][i]; if(!in_queue[i]) { my_queue.push(i); in_queue[i]=true; } pre[i]=temp; max_flow[i]=MIN(max_flow[temp],(map[temp][i]-flow[temp][i]));//求得max_flow } } in_queue[temp]=false; } if(pre[sink]!=-1) return true;//sink的父节点不为初始值，说明已经找到了一条路径 return false; }int sum_cost,sum_flow;//final ans void min_cost_max_flow(int num,int source,int sink){ sum_cost=0,sum_flow=0; memset(flow,0,sizeof(flow)); while(SPFA(num,source,sink))//while(can find a path from s to t with its cost<INF) { int k=sink; while(pre[k]!=-1) //find from sink point to source point { flow[pre[k]][k]+=max_flow[sink]; //positive edge+=new flow flow[k][pre[k]]=-flow[pre[k]][k]; //nagative edge-=new flow k=pre[k]; } sum_cost+=dist[sink]; //min cost sum_flow+=max_flow[sink]; //max flow with minimal cost } } int main() { int N,M,ans,i,j; char temp[MAXN]; int house[MAXN][2],house_index; int people[MAXN][2],people_index; //freopen("2195.in","r",stdin); while(scanf("%d%d",&N,&M)!=EOF&&N&&M) { memset(map ,0,sizeof(map)); memset(cost,0,sizeof(cost)); house_index=0; people_index=0; for(i=0;i<N;i++) { scanf("%s",temp); for(j=0;j<M;j++) { if(temp[j]=='H') { house[house_index][0]=i; house[house_index][1]=j; house_index++; } else if(temp[j]=='m') { people[people_index][0]=i; people[people_index][1]=j; people_index++; } } } for(i=0;i<people_index;i++) { for(j=0;j<house_index;j++) { cost[i][people_index+j]=abs((people[i][0]-house[j][0]))+abs((people[i][1]-house[j][1])); cost[people_index+j][i]=-cost[i][people_index+j];//record nagative road's value be oppsite of positive road map[i][people_index+j]=1; } map[people_index+house_index][i]=1;//super source point map[house_index+i][people_index+house_index+1]=1; //super sink point } min_cost_max_flow(people_index+house_index+2,people_index+house_index,people_index+house_index+1); //min_cost_max_flow(int num,int source,int sink) printf("%d/n",sum_cost); //printf("%d/n",sum_flow); } return 0; }