快速傅氏变换之旅(四) 第一个别人的例子解读

转载请标明是引用于 http://blog.csdn.net/chenyujing1234

 例子代码:(编译工具：VS2005)

 http://www.rayfile.com/zh-cn/files/2a34ba02-7ba4-11e1-b624-0015c55db73d/

外语文章:http://www.codeproject.com/Articles/9388/How-to-implement-the-FFT-algorithm

 

介绍:

此文章描述了执行1D版本的为复数数组的FFT算法的方法.

目的是展示一种高效的快速FFT算法，它能容易地根据用户修改。

当我在开发一个根据捕获的声音做出频谱的应用软件时我已经学习过FFT算法.

 

背景

首先，里面95%的代码不是我写的，这是1982年的书本<<数值分析>>里摘录的。

但这也加入我的一些改进。我已经能够在代码基础上改进算法，这样O()(测量算法复杂度的单位)减少到了N计算。

 

The FFT

首先我们定义FFT函数.

//data -> float array that represent the array of complex samples//number_of_complex_samples -> number of samples (N^2 order number) //isign -> 1 to calculate FFT and -1 to calculate Reverse FFTfloat FFT (float data[], unsigned long number_of_complex_samples, int isign){    //variables for trigonometric recurrences    unsigned long n,mmax,m,j,istep,i;    double wtemp,wr,wpr,wpi,wi,theta,tempr,tempi;

 

The Big-Reversal Method

首先，原始的数组一定要被转化，目的是能表现Danielson-Lanzcos算法。

比如complex[index]将和complex[bit-reverse-order-index]交换位置，如果index是0b00001,bit-reverse-order-index将会是0b10000
这个方法是:

    //复数数组是 real+complex,所以作为一个大小为n = 2*number的数组    // 实数部分是 data[index] 虚数部分是 data[index+1]    n=number_of_complex_samples * 2;     //binary inversion (note that     //the indexes start from 1 witch means that the    //real part of the complex is on the odd-indexes    //and the complex part is on the even-indexes    j=1;    for (i=1;i<n;i+=2)     {         if (j > i){            //交换实数部分            SWAP(data[j],data[i]);             //交换虚数部分            SWAP(data[j+1],data[i+1]);        }        m=n/2;        while (m >= 2 && j > m){            j -= m;            m = m/2;        }        j += m;    }

 

#defineSWAP(a,b)tempr=(a);(a)=(b);(b)=tempr//tempr is a variable from our FFT function

从下图可以看到对转化的数据数组做了什么

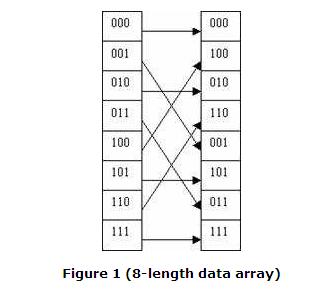
请看上面图：
用一个mirror把数组分为两部分，

左边与右边相同部分用线映射。

镜像效应允许你在数组的第一半上做bit-reversal方法,

并且直接在另一半上面用它。但你必须小心一件事情：

如果改变发生在左半部分，那么你仅能应用此效应。这意味着，

如果改变是在左边部分的index与别边部分的index间，那么这个

方法是不可用的，否则你会做交换之后重新做它。（如果用在

16个数上你就会发现我说的情况).

所以代码应该变成:

 

//the complex array is real+complex so the array     //as a size n = 2* number of complex samples    // real part is the data[index] and     //the complex part is the data[index+1]    n=number_of_complex_samples * 2;     //binary inversion (note that the indexes     //start from 0 witch means that the    //real part of the complex is on the even-indexes     //and the complex part is on the odd-indexes    j=0;    for (i=0;i<n/2;i+=2) {        if (j > i) {            //swap the real part            SWAP(data[j],data[i]);            //swap the complex part            SWAP(data[j+1],data[i+1]);            // checks if the changes occurs in the first half            // and use the mirrored effect on the second half            if((j/2)<(n/4)){                //swap the real part                SWAP(data[(n-(i+2))],data[(n-(j+2))]);                //swap the complex part                SWAP(data[(n-(i+2))+1],data[(n-(j+2))+1]);            }        }        m=n/2;        while (m >= 2 && j >= m) {            j -= m;            m = m/2;        }        j += m;    }

 

The Danielson-Lanzcos

它应用了N*log2(N)三角函数。

 //Danielson-Lanzcos routine     mmax=2;    //external loop    while (n > mmax)    {        istep = mmax<<  1;        theta=sinal*(2*pi/mmax);        wtemp=sin(0.5*theta);        wpr = -2.0*wtemp*wtemp;        wpi=sin(theta);        wr=1.0;        wi=0.0;        //internal loops        for (m=1;m<mmax;m+=2) {            for (i= m;i<=n;i+=istep) {                j=i+mmax;                tempr=wr*data[j-1]-wi*data[j];                tempi=wr*data[j]+wi*data[j-1];                data[j-1]=data[i-1]-tempr;                data[j]=data[i]-tempi;                data[i-1] += tempr;                data[i] += tempi;            }            wr=(wtemp=wr)*wpr-wi*wpi+wr;            wi=wi*wpr+wtemp*wpi+wi;        }        mmax=istep;    }

 

如何使用FFT

想象你要去收集一个信号的采样，且你想要去知道它的基本频率，

采样能从任何的源采集到：你插到代码里的函数、捕获的声音片等.......

可以说信号是一个数组信息（就像捕获的声音buffer）,我们如何做FFT呢？

首先你要去选择你用的FFT变量，假设我们有一个指定的变量了，虽然它不是最有效的，

但是是最简单的。

下一个关心的是你将要发送给FFT的数据的数量和采样率，采样率必须是2^N数量。

但它不需要去发送一个2^N个采样去处理(为不同的执行的0真实的NR).

比如你仅能发送50个采样，并用0填充剩下的采样，但是，记住，你发送更多的数据来计算，FFT精度越高。

 

 

结果

在FFT被计算后，你能用复数数组来提取出结论。

如果你对信息的基本频率有兴趣，那么找到数组中的绝对值的最大值，且频率将按数组的index被给。

复数的绝对值是实部的平方与虚部平方的和开根。

如果最大绝对值是在复数数组中的[102][103]（real,complex），那么你的基本频率是102/2=61HZ。

你得除以2，因为数组是两倍大小的（因为有实部与虚部），所以结果不是102,而是61.

如果你想要去画傅丽叶信号，那么它也是同样的方法。频率30通过复数[30][31].。。。。的绝对值被给出。

计算出来的FFT的第二部分一定要被忽略，因为尼奎斯特定理冗余（最小的采样率要是最高频率的两倍）。

它仅是第一部分的镜像。如果你想测量的频率高达6000，你需要用2^N为2*6000.

在我的例子里，我在CClidView类的OnPain函数里,用了FFT转为正弦信号。FFT在CFourier类中被执行。