矩阵范数/谱/条件数

来源：互联网发布：创业软件股票最新消息编辑：程序博客网时间：2024/05/17 08:23

一、向量和矩阵范数直观概念

在实数域中，数的大小和两个数之间的距离是通过绝对值来度量的。在解析几何中，向量的大小和两个向量之差的大小是“长度”和“距离”的概念来度量的。为了对矩阵运算进行数值分析，我们需要对向量和矩阵的“大小”引进某种度量。范数是绝对值概念的自然推广。

"范数"是对向量和矩阵的一种度量,实际上是二维和三维向量长度概念的一种推广.

二、矩阵范数

矩阵范数（martix norm）是数学上向量范数对矩阵的一个自然推广。

-------------------------------------------------------------------

NORM   Matrix or vector norm.
    For matrices...
      NORM(X) is the largest singular value of X, max(svd(X)).
      NORM(X,2) is the same as NORM(X).
      NORM(X,1) is the 1-norm of X, the largest column sum,
                      = max(sum(abs(X))).
      NORM(X,inf) is the infinity norm of X, the largest row sum,
                      = max(sum(abs(X'))).

-------------------------------------------------------------------

在 p = 1 且 $p=\infty$ 的情况下，其范数可以以下方式计算：

$\begin{align}& \left \| A \right \| _1 = \max \limits _{1 \leq j \leq n} \sum _{i=1} ^m | a_{ij} | \\& \left \| A \right \| _\infty = \max \limits _{1 \leq i \leq m} \sum _{j=1} ^n | a_{ij} | .\end{align}$
若满足 p = 2（欧几里德范数）且 m = n（方阵）此两特殊情况时，诱导的矩阵范数就是“谱范数”。矩阵 A 的谱范数是 A 最大的奇异值或半正定矩阵 A*A 的最大特征值的平方根：: $\left \| A \right \| _2=\sqrt{\lambda_{\text{max}}(A^* A)}$
其中 A* 代表 A 的共轭转置。

任何矩阵范数满足此不等式

$\left \| A \right \| \ge \rho(A),$

其中 ρ(A) 是 A 的谱半径。事实上，可以证明 ρ(A) 是 A 的所有诱导范数的下界。
此外，我们有

$\left \| A \right \| \ge \rho(A),$

-------------------------------------------------------------------

三、谱半径

设A是n × n矩阵，λi是其特征值，i = 1，2，……，n。称ρ(A)=max{|λi|,i=1,2,……n}为A的谱半径。
即矩阵A的谱半径等于矩阵A的特征值绝对值的最大值。

-------------------------------------------------------------------

在matlab中求谱半径方法：

%Spectral radius
%本函数用来求谱半径
function t=rho(A)
t=max(abs(eig(G)));
end

四、矩阵A的条件数

矩阵A的条件数等于A的范数与A的逆的范数的乘积，即cond(A)=‖A‖·‖A-1‖。

$\kappa (A) = \Vert A^{-1}\Vert \cdot \Vert A\Vert.$

* 若 $\|\cdot\|$ 是 l2 矩阵范数则
$\kappa(A) = \frac{\sigma_{max}(A)}{\sigma_{min}(A)}$
其中σmax(A)和σmin(A)分别是A的极大和极小奇异值。

因此

        * 若A是正规矩阵则

     $\kappa(A) = \left|\frac{\lambda_{max}(A)}{\lambda_{min}(A)}\right|$
( $\lambda_{max}(A),\ \lambda_{min}(A)$ 分别是A的极大和极小特征值（根据模数））

        * 若A是酉矩阵则

        κ(A) = 1

-------------------------------------------------------------------

COND   Condition number with respect to inversion.
    COND(X) returns the 2-norm condition number (the ratio of the
    largest singular value of X to the smallest). Large condition
    numbers indicate a nearly singular matrix.

    COND(X,P) returns the condition number of X in P-norm:

       NORM(X,P) * NORM(INV(X),P).

where P = 1, 2, inf, or 'fro'.

-------------------------------------------------------------------

矩阵A的条件数等于A的范数与A的逆的范数的乘积，即cond(A)=‖A‖·‖A-1‖，对应矩阵的3种范数，相应地可以定义3种条件数。函数 cond(A,1)、cond(A)或cond(A) 是判断矩阵病态与否的一种度量，条件数越大矩阵越病态。

五、奇异值：

the singular values of a compact operator T : X → Y acting between Hilbert spaces X and Y, are thesquare roots of the eigenvalues of the nonnegative self-adjoint operator T*T : X → X (where T* denotes the adjoint of T).

-------------------------------------------------------------------
六、正规矩阵
在数学中，正规矩阵 A 是与自己的共轭转置交换的复数方块矩阵，也就是说， A 满足
$\mathbf{A}^* \mathbf{A} = \mathbf{A} \mathbf{A}^*$
其中A* 是A 的共轭转置。

如果A* 是实系数矩阵，那么条件简化为
$\mathbf{A}^T \mathbf{A} = \mathbf{A} \mathbf{A}^T$
其中 {A}^T 是A 的转置矩阵。
-------------------------------------------------------------------
酉矩阵

若一n行n列的复数矩阵U满足

$U^* U = UU^* = I_n\,$

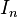其中 $I_n\,$ 为n阶单位矩阵，U*为U的共轭转置，为酉矩阵(英文:Unitary Matrix, Unitary 是归一或单位的意思)。即，矩阵U为酉矩阵，当且仅当其共轭转置U*为其逆矩阵:

$U^{-1} = U^* \,\;$ 。

-------------------------------------------------------------------

如果λ是矩阵A的特征值，那么1/λ是inv(A)的特征值。

Ax=λx

则

inv(A)Ax=inv(A)λx 即

x/λ=inv(A)x

条件数是判断矩阵病态与否的一种度量，条件数越大矩阵越病态。

一个低条件数的问题称为良置的，而高条件数的问题称为病态（或者说非良置）的。

条件数事实上表示了矩阵计算对于误差的敏感性。对于线性方程组Ax=b，如果A的条件数大，b的微小改变就能引起解x较大的改变，数值稳定性差。如果A的条件数小，b有微小的改变，x的改变也很微小，数值稳定性好。它也可以表示b不变，而A有微小改变时，x的变化情况。
比如线性方程组
〔1     2   [x   = [4
3.999 1]   y]      7.999]
的解是(x,y)=(2,1),
而
〔1     2   [x   = [4.001
3.999 1]   y]      7.998]
的解是(x,y)=(-3.999,4.000)
可见b很小的扰动就引起了x很大的变化，这就是A矩阵条件数大的表现。
一个极端的例子，当A奇异时，条件数为无穷，这时即使不改变b，x也可以改变。奇异的本质原因在于矩阵有0特征值，x在对应特征向量的方向上运动不改变Ax的值。如果一个特征值比其它特征值在数量级上小很多，x在对应特征向量方向上很大的移动才能产生b微小的变化，这就解释了为什么这个矩阵为什么会有大的条件数，事实上，正规阵在二范数下的条件数就可以表示成 abs(最大特征值/最小特征值)。