谈求面积的Pick 公式

来源：互联网发布：suse linux安装grub 编辑：程序博客网时间：2024/04/27 17:53

谈求面积的Pick 公式

蔡聪明

问题的起源
一维的特例：植树问题
推广到二维平面
Pick 定理的证明
Pick 定理的推广
其他的求面积公式

Pick 公式、Heron 公式与测量师公式，是数学里求面积的三个重要公式。本文我们着重在讨论其中的Pick公式，从问题出发到猜测、发现、检验与证明等的发展过程，内容浅白，高中生亦可研读。

问题的起源

好奇与实用是数学发展的动力，两者相辅相成，不可偏废。

古埃及人铺地板时，用同一种大小的正多边形，结果只能是正三角形、正方形与正六边形所铺成的三种样式（见图一、二及三）。

图一：用正三角形铺地板

图二：用正方形铺地板

图三：用正六边形铺地板

这媲美于正多面体恰好有五种，都是很令人惊奇的结果。为了追究背后的原因，他们发现了「三角形三内角和为一平角(即 $180^{\circ}$ )定理」，由此证明出铺地板恰有三种样式，从而对经验事实求得解释(explanation)。

进一步，在正方形样式的地板上[即平面正方形格子网或几何板(geoboard)]，古埃及人又从中玩索出毕氏定理(见图四)，以及其他许多几何定理。在验证毕氏定理时，涉及了需计算以格子点为顶点的正方形之面积。

另一方面，基于实际应用，如农夫在田地上插秧或种植果树(假设种在正方形的格子点上)。显然，田地越广，所种的棵数就越多，反之亦然。因此，土地的面积与棵数具有密切的关系，但这个关系是什么呢？

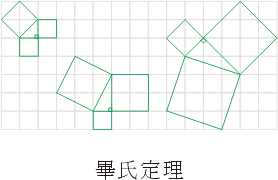
图四：毕氏定理

不论是起于好奇或实用，都引出了下面一个有趣的数学问题：

问题：平面上以格子点为顶点的多边形，其面积公式是什么呢？如何探寻它？（见图五）

图五：以格子点为顶点的任一多边形

本文我们就来探讨这个问题。它从发现到证明的过程，都富有思考方法的启发性，值得追寻。

谈求面积的Pick公式（第2页）

蔡聪明

一维的特例：植树问题

要追寻一个公式或规律，通常是由特例着手。一个问题的特例，正如其推广或类推，往往有各种式样。换言之，一个问题并非是孤立的，而是座落在由许多问题所连结起来的四通八达的网路上。例如，在上述问题中，将多边形改为三角形或长方形，就是一个特例的思考方向。也可以将二维平面的问题，改为一维的直线问题，这又是另一个特例的思考方向。找到一个适当的特例，由此切入，逐步寻幽探径，发现其一般规律后，从而解决整类的问题，这是最令人欣喜的事情。

我们选择一维的特例来思考，此时不过是简单的植树问题。例如：在图六的线段上每隔单位距离种一棵树（即在格子点上种树），两端皆种，问线段有多长？

图六：一维的植树问题

我们观察到格子点可分成内点(interior points)与边界点(boundary points)两类。假设内点与边界点的个数分别为i与b（事实上b =2）。显然线段之长L为：

L= $\displaystyle \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 200}\hski... ....0pt plus0.2pt minus0.1pt{\fontfamily{cwM1}\fontseries{m} \selectfont \char 98}}$ 1 =i +12 =b + i -13

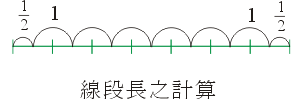
我们也可以这样想：如果在相邻两格子之中点加以分割，得到许多小段，那么每一个内点所在的小段皆具有单位长度，而每一个边界所在的小段只有 $\frac{1}{2}$ 单位长度，见图七。换言之，一个内点贡献一个单位长度，而一个边界点只贡献 $\frac{1}{2}$ 个单位长度。因此，线段的长度为：

$\begin{displaymath}L=\frac{b}{2}+i\eqno{(4)}\end{displaymath}$

图七：线段长之计算

谈求面积的Pick公式（第3页）

蔡聪明

推广到二维平面

对于平面上以格子点为顶点之多边形，其面积公式是什么呢？在上述(1)～(4)的公式中，只有(3)与(4)两式比较有可能。因此，我们初步猜测多边形的面积A为：

$\begin{displaymath}A=b+i-1\eqno{(5)}\end{displaymath}$

或者

$\begin{displaymath}A=\frac{b}{2}+i\eqno{(6)}\end{displaymath}$

其中b与i分别表示在多边形中，边界点与内点之格子点个数。

接着是用一些例子对猜测作试验。因为多边形有无穷多种，所以即使试验再多的例子都成立，这都不能代表已证明出我们的猜测，但是只要有一个例子违背（称之为反例），就否定掉猜测。举例而言，「凡是天鹅都是白色的」，我们观察过再多的白色天鹅都无法得到证明，但是只要出现一只黑天鹅就否定掉这句话了。这种证明和否证的不对称性值得注意。

图八

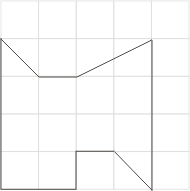
图九

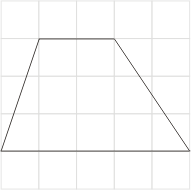
图十

现在，我们试验图八、九与十等三个例子，列表如下：

(I) b(II) i(III) b + i -1(IV) $\frac{b}{2}+i$ (V) $\mbox{\hskip 1.2pt plus0.4pt minus0.2pt{\fontfamily{cwM1}\fontseries{m}\selectf... ...0.0pt plus0.2pt minus0.1pt{\fontfamily{cwM2}\fontseries{ m}\selectfont \char 9}}$ 10211761752113 $\frac{1}{2}$ 12 $\frac{1}{2}$ 971611 $\frac{1}{2}$ 10 $\frac{1}{2}$

比较(III)与(V)行，(IV)与(V)行,我们发现公式(5)与(6)都不对。该如何修正呢?

我们进一步观察到(IV)与(V)两行有规律，即相差1，所以我们将(6)式修正为

$\begin{displaymath} A=\frac{b}{2}+i-1\eqno{(7)} \end{displaymath}$

这个面积公式就「适配」(fit) 上述图八至图十的三个例子。

我们也可以从另一个角度来观察(7)式。仿照一维植树问题的情形，考虑图十一之长方形。我们发现，一个内点贡献面积1，而边界点分成两种情形：

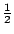: (i)在侧边上的点，每一点贡献面积 $\frac{1}{2}$ ；
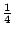: (ii)四个顶点，每一点贡献面积 $\frac{1}{4}$ 。

因此，如果每一个边界点都看成是贡献面积 $\frac{1}{2}$ ，则整个合起来就多算了一个单位面积，必须扣掉。换言之，(7)式是一个合理的猜测。

图十一

再对(7)式作试验，例如考虑图十二、十三与十四，容易求得它们的正确面积分别为 $4\frac{1}{2}$ 、13与 $12\frac{1}{2}$ 。另一方面，按公式(7)来计算，分别得到 $4\frac{1}{2}$ 、13与13。因此，对于图十二与十三而言，(7)式成立；但是对于图十四，(7)式就不成立了。我们发现图十四比较特别，有两个边交叉了，这并不是通常所谓的多边形。如果将这种情形排除掉，只允许边没有交又的情形，我们称之为单纯多边形(simple polygon)，那么我们猜测(7)式对于单纯多边形都会成立。

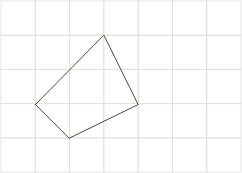
图十二

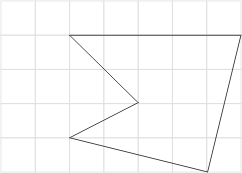
图十三

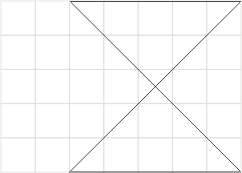
图十四

岂其然乎？我们用了更多不同形状的单纯多边形作试验，结果发现(7)式都成立（读者应该自己尝试）。至此，我们更有理由相信，(7)式很可能就是我们所要追寻的公式。下一步，也许该尝试去证明它了。

(7)式有各种证明方法，本文我们只介绍两种证法。

谈求面积的Pick公式（第4页）

蔡聪明

Pick 定理的证明

一般而言，数学是先有观察与猜测（这个阶段允许犯错），然后才有试验、修正与证明。数学绝不是突然(out of the blue) 从天上掉下一个公式或定理，然后就要我们去证明。通常数学教科书所犯的毛病就是按「定义、定理、证明，等抽象方式来铺陈，这样无法看到数学的发展过程。

为了证明(7)式，首先让我们分析单纯多边形:

(i)最简单的单纯多边形就是原子三角形(atomic or primitive triangles)，亦即除了三个顶点之外，三边及内部皆不含格子点之三角形，见图十五，其面积皆为 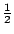$\frac{1}{2}$ ，并且可用(7)式来计算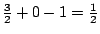： $\frac{3}{2}+0-1=\frac{1}{2}$ 。因此，对于原子三角形，上述(7)式成立。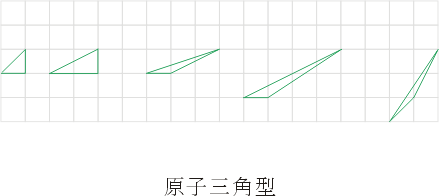

图十五：原子三角形

(ii) 其次，我们观察到，对于任意的单纯多边形都可以先分割成三角形（即三角形化），再进一步分割成原子三角形之组合(这叫做原子化)，见图十六。

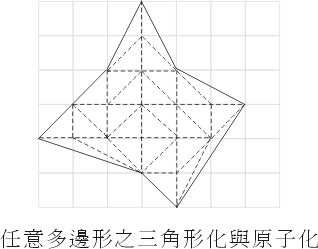
图十六：任意多边形之三角化与原子化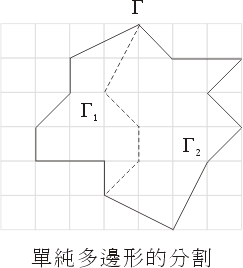

图十七：单纯多边形的分割

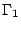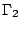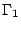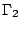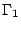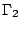(iii)最后考虑任何单纯多边形Γ将它分割成两个单纯多边形 $\Gamma_1$ 与 $\Gamma_2$ ，见图十七。设Γ有b个边界点、i个内点，并且 $\Gamma_1$ 与 $\Gamma_2$ 分别有b ₁个与b ₂个边界点、有i₁个与i ₂个内点。再设 $\Gamma_1$ 与 $\Gamma_2$ 有b ₃个共同的边界点，则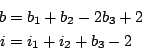

$\begin{eqnarray*} b&=&b_1+b_2-2b_3+2\\ i&=&i_1+i_2+b_3-2 \end{eqnarray*}$

所以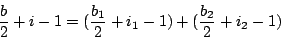

$\begin{displaymath} \frac{b}{2}+i-1=(\frac{b_1}{2}+i_1-1)+(\frac{b_2}{2}+i_2-1) \end{ displaymath}$

因此，公式(7)在分割下，具有加性(additivity)。

上述三个步骤综合起来，我们就证明了(7)式，一旦猜测有了证明，就成为定理。

定理一：Pick 定理，1899年

设Γ 为平面上以格子点为顶点之单纯多边形，则其面积为

$\begin{displaymath} A=\frac{b}{2}+i-1\eqno{(8)} \end{displaymath}$

其中b为边界上的格子点数，i为内部的格子点数。(8)式叫做Pick公式。

在上述证明中，单纯多边形经过原子化后，成为一个连通的平面图枝(a connected plane graph)。著名的尤拉(Euler) 公式告诉我们，对于任何连通的平面图枝（不限于格子点图枝）恒有：

$\begin{displaymath}V-E+F=2\eqno{(9)}\end{displaymath}$

其中V表示图枝的顶点(vertices)个数（即V = b + i），E表示棱线(edges)的个数，F表示平面被图枝分割所成的块数（其中最外的一块是无界的）。例如，在图十六中，V =20 , E =49 , F =31。

因为每一个原子三角形的面积为 $\frac{1}{2}$ ，并且总共有F -1个，所以原来单纯多边形的面积为：

$\begin{displaymath} A=\frac{1}{2}(F-1)\eqno{(10)} \end{displaymath}$

由尤拉公式与V = b + i得到：

$\begin{displaymath} A=\frac{1}{2}-\frac{b}{2}-\frac{i}{2}+\frac{E}{2}\eqno{(11)} \ end{displaymath}$

再由Pick 公式，可知：

$\begin{displaymath} \frac{1}{2}-\frac{b}{2}-\frac{i}{2}+\frac{E}{2}=\frac{b}{2}+ i-1 \end{displaymath}$

于是我们得到棱线的个数为：

$\begin{displaymath} E=2b+3i-3\eqno{(12)} \end{displaymath}$

事实上，这个公式对于一般连通的三角形化的平面图枝（不限于格子点图枝）都成立。

定理二：（棱线定理，Edge Theorem）

对于任意连通的三角形化的平面图枝，其棱线的个数恒为

$\begin{displaymath}E=2b+3i-3\eqno{(13)}\end{displaymath}$

其中b与i分别表示图枝边界上的顶点数与内部的顶点数。

证明：我们分成三个步骤：

(i)最简单的情形是b =3，i =0，图枝只含一个三角形，此时E =3，故公式(13)成立。

(ii)若在三角形的内部增加一个顶点，则E增加3。此时(13)式也成立。

(iii)假设一个连通的三角形化的平面图枝满足(13)式（即E =2 b +3 i-3），今在其外部增加一个新的边界顶点，使得原来图枝的边界顶点有m个变成内部顶点（m可能等于0），则E增加m +2。于是由E =2 b +3 i-3得：

E + m +2=2( b +1- m )+3( i + m )-3

换言之，对于新的图枝而言，(13)式仍然成立。按数学归纳法，我们就证明了(13)式。

由棱线定理与尤拉公式，我们也可以推导出Pick 定理，这就是下面要介绍的Pick 定理之第二种证法：

根据V = b + i , E =3 i +2 b -3 , V - E + F =2，以及面积 $A=\frac{1}{2}(F-1)$ ，立即可算得：

$\begin{displaymath} A=\frac{b}{2}+i-1 \end{displaymath}$

反过来，由Pick 定理与棱线定理也可以推导出尤拉公式（见参考资料7）。

由Pick 定理知，以格子点为顶点之多边形，其面积必为有理数，但是正三角形的面积为无理数，所以我们有了

: 推论：以格子点为顶点之正三角形不存在。

事实上，我们可以证得一般结果，如下:

: 定理三：正方形是唯一以格子点为顶点之正多边形。

谈求面积的Pick公式（第5页）

蔡聪明

Pick 定理的推广

一个好的数学结果，除了定理本身漂亮之外，更要紧的是它要具有推广的潜力，能在许多相关结果中占有枢纽的地位。Pick 定理就具有这样的推广潜力。

Pick 定理有许多方向的推广。例如，它可以推广到更一般的多边形，边可以交叉，中间可以挖掉多边形；也可以推广到不同形式的格子点，如正六边形格子点;更可推广到三维空间的多面体之情形。

本文我们不讨论这些推广，仅列出参考资料，供有兴趣的读者进一步去追寻。

．原载于科学月刊第二十五卷第十期
．作者当时任教于台大数学系

http://episte.math.ntu.edu.tw/articles/sm/sm_25_10_1/index.html