poj 2528 （线段树_离散化）

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
  
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
  
• The wall is divided into segments and the width of each segment is one byte. 
  
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

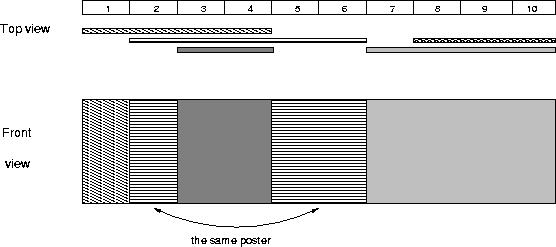
The picture below illustrates the case of the sample input. 

Sample Input

151 42 68 103 47 10

Sample Output

4

题目大意：在一个公告栏上面张贴海报；张贴之后问可以看到几张海报

题目分析：线段树问题，但是如果以一个点为叶子节点的话就会超时妥妥的，所以采用离散化思想，首先将所有的点进行排序；用一个数组来进行对应，下标对应实际坐标，下标对应的数字表示离散化之后的坐标，通过离散化之后的坐标可以建立线段树

代码：

#include <iostream>#include<cstdio>#include<algorithm>#include<cmath>using namespace std;struct code{    int r;int l;}p[50005];bool tree[50010*4];///这个树的定义是是否这个区间被覆盖；void build ( int p,int l,int r){    if ( l == r ) {tree[p] = true; return;}///将所有区间赋值为没有被覆盖    int mid = ( l + r ) >> 1;    build ( 2 * p, l, mid);    build ( 2 * p + 1,mid + 1, r);    tree[p] = tree[p*2]||tree[p*2+1];}bool post(int p,int l,int r, int sl, int sr){    if ( tree[p] == 0 ) return false;    if ( sl <= l&& sr >= r )    {        tree[p] = false;        return true;    }    int mid = ( l + r ) >> 1;    bool ok = 0;    if ( sl <= mid ) ok = post( 2 * p , l , mid, sl , sr )||ok;///如果左边区间有值的话在左边区间查询    if ( sr > mid ) ok = post( 2 * p + 1, mid + 1, r, sl, sr )||ok;///如果右边区间有值的话在右边区间查询    tree[p] = tree[p*2]||tree[p*2+1];    return ok;}int x[50005 << 1];int hashs[10000002];int posts;int main(){    //freopen("in.txt","r",stdin);    int test;    scanf ( "%d",&test);    while ( test > 0 )    {        test--;        scanf("%d",&posts);        int counts = 0;        for ( int i = 0; i < posts; i++ )        {            scanf("%d %d",&p[i].l,&p[i].r);            x[counts++] = p[i].l;            x[counts++] = p[i].r;        }        sort(x,x+counts);        counts = unique(x,x+counts) - x;///变量去重        int node = 0;        for ( int i = 0; i < counts; i++ )        {            hashs[x[i]] = node;///将所有的点进行对应，下标表示原来的坐标，下标对应的数字应该是离散化之后的坐标            if ( i < counts - 1 )            {                if ( x [i+1] - x [i] == 1 )                    node++;                else                    node+=2;                ///如果两个变量之间的坐标差值超过1的话就要将中间的区间离散化进去；                ///如果为1 10；1 4；5 10；和 1 10；1 4；6 10；如果第二种情况四和六之间差值大于1，如果不将中间的                ///5离散化之后就会将第一种情况和第二种情况计算为2；            }        }        build ( 1, 0,node);///建树的时候要注意区间是从0到node的这个区间是左闭右闭；        int ans = 0;        for ( int i = posts-1; i >= 0; i--)        ///这里是将所有的海报倒着循环，也就是说如果前面的海报的所有地方被后面的海报占的话就不能显示出来了        {            if (post (1,0,node,hashs[p[i].l],hashs[p[i].r]))                ans++;        }        printf ("%d\n",ans);    }}