POJ 1230 Pass-Muraille

POJ 1230

Pass-Muraille

Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 9454 Accepted: 2934

Description

In modern day magic shows, passing through walls is very popular in which a magician performer passes through several walls in a predesigned stage show. The wall-passer (Pass-Muraille) has a limited wall-passing energy to pass through at most k walls in each wall-passing show. The walls are placed on a grid-like area. An example is shown in Figure 1, where the land is viewed from above. All the walls have unit widths, but different lengths. You may assume that no grid cell belongs to two or more walls. A spectator chooses a column of the grid. Our wall-passer starts from the upper side of the grid and walks along the entire column, passing through every wall in his way to get to the lower side of the grid. If he faces more than k walls when he tries to walk along a column, he would fail presenting a good show. For example, in the wall configuration shown in Figure 1, a wall-passer with k = 3 can pass from the upper side to the lower side choosing any column except column 6. 

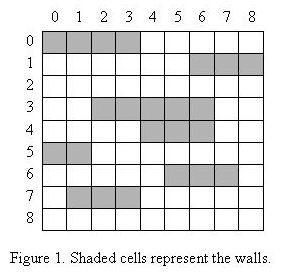
Given a wall-passer with a given energy and a show stage, we want to remove the minimum number of walls from the stage so that our performer can pass through all the walls at any column chosen by spectators. 

Input

The first line of the input file contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case contains two integers n (1 <= n <= 100), the number of walls, and k (0 <= k <= 100), the maximum number of walls that the wall-passer can pass through, respectively. After the first line, there are n lines each containing two (x, y) pairs representing coordinates of the two endpoints of a wall. Coordinates are non-negative integers less than or equal to 100. The upper-left of the grid is assumed to have coordinates (0, 0). The second sample test case below corresponds to the land given in Figure 1. 

Output

There should be one line per test case containing an integer number which is the minimum number of walls to be removed such that the wall-passer can pass through walls starting from any column on the upper side. 

Sample Input

23 12 0 4 00 1 1 11 2 2 27 30 0 3 06 1 8 12 3 6 34 4 6 40 5 1 55 6 7 61 7 3 7

Sample Output

11

Hint

Walls are parallel to X.

Source

Tehran 2002 Preliminary

题意：

魔术师前方有 n 堵墙，而他每次最多能跳过 k 堵墙，求拆掉最少的墙，使他在任意列都能一次跳过所有的墙。

贪心，从左向右遍历当前列的墙的个数，假设当前列的墙数超过了 k 堵，拆，开始想的把在当前列的长度最大的墙拆了

后来想想，当前列前面的墙无论多长都没有什么影响，所以，

每次选择所在当前列的墙中右端点最大的删除，这样才能对后面的影响最小，

使后面拆的墙数最少，为最优方案。

代码：

#include <cstdio>#include <cstring>#include <iostream>#include <algorithm>using namespace std;struct wall{    int x1, y1, x2, y2, ok; //ok记录墙是否拆了，1表示未拆，0表示拆了} W[110];int main(){    int t, n, k;    scanf("%d", &t);    while(t--)    {        scanf("%d%d", &n, &k);        int mx = 0;             //记录所有墙的最右端点        for(int i = 0; i < n; i++)        {            scanf("%d%d%d%d", &W[i].x1, &W[i].y1, &W[i].x2, &W[i].y2);            if(W[i].x1 > W[i].x2) swap(W[i].x1, W[i].x2);   //刚开始没写，坑我WA一次            W[i].ok = 1;                    //标记所有的墙都未拆            mx = max(mx, W[i].x2);        }        int sum = 0;        for(int i = 0; i <= mx; i++)    //判断点 i 所在列有几堵墙        {            int cnt = 0;            for(int j = 0; j < n; j++)                if(i >= W[j].x1 && i <= W[j].x2 && W[j].ok == 1) cnt++;            if(cnt <= k) continue;      //墙数不超过k，继续判断下一列            cnt -= k;        //删除 cnt 个墙            sum += cnt;            while(cnt--)            {                int End = 0, id = 0;        //贪心，这里删除满足条件的右端点最大的墙                for(int k = 0; k < n; k++)                    if(W[k].ok == 1 && i >= W[k].x1 && i <= W[k].x2 && W[k].x2 > End)                    {                        id = k;                        End = W[k].x2;                    }                W[id].ok = 0;            }        }        printf("%d\n", sum);    }    return 0;}