熵 (Entropy)
来源:互联网 发布:大数据架构师简历 编辑:程序博客网 时间:2024/05/31 19:26
李天岩
- 1. Shannon 熵
- 2. Kolmogorov 熵
- 3. 拓樸熵 (Topological Entropy)
- 4. Boltzmann 熵
在我們日常生活中,似乎經常存在看「不確定性」的問題。比方說,天氣預報員常說「明天下雨的可能性是 70%。這是我們習以為常的「不確定性」問題的一個例子。一般不確定性問題所包含「不確定」(uncertainty) 的程度可以用數學來定量地描述嗎?在多數的情況下是可以的。本世紀40年代末,由於信息理論 (information theory) 的需要而首次出現的 Shannon 熵,50年代末以解決遍歷理論 (ergodic theory) 經典問題而嶄露頭角的 Kolmogorov 熵,以及60年代中期,為研究拓樸動力系統 (topological dynamical system) 而產生的拓樸熵 (topological entropy) 等概念,都是關於不確定性的數學度量。它們在現代動力系統和遍歷理論中,扮演看十分重要的角色。在自然科學和社會科學中的應用也日趨廣泛。本文的主旨在於引導盡量多的讀者在這一引人入勝的領域中尋幽訪勝,而不必在艱深的數學語言中躑躅不前。物理、化學家們也許對他們早已熟悉的熱力學熵更覺親切。我們在最後一節也將給古典的 Boltzmann 熵作一番數學的描述。
設想我們有兩枚五分硬幣,一枚硬幣表面光滑,材料均勻,而另一枚硬幣則表面粗糙,奇形怪狀。我們把硬幣上有人頭的那面叫正面,另一面稱反面。然後在一個光滑的桌面上旋轉硬幣,等它停下來後,看是正面或是反面。這是一個不確定性的問題:可能是正面,可能是反面。第一枚硬幣,由於正面和反面的對稱性,正面或反面朝上的機率各為一半。但對第二枚硬幣來說,由於材料磨損,正面和反面不再對稱。可能正面朝上的機率為 70%,反面朝上的機率為 30%。對「究竟會是正面?或會是反面?」這一不確定性問題來說,第一枚硬幣「不確定」的程度顯然比第二枚硬幣要大了許多。若要下賭注的話,我想還是下第二枚硬幣的正面朝上,較為保險,不是嗎?現在假設鑄幣局的先生們別出心裁,把硬幣設計成圖1-1所示的形狀,其上為正,其下為反,則無論我們怎樣旋轉它,最終總是正面朝上。它「不確定」的度量應該為零-其結果在未旋轉前都已確定,那來什麼「不」確定度呢?
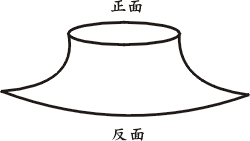
圖1-1
有了這些直接的觀察,我們可以在數學上做文章了。假設樣本空間 (Sample space) X 有 n 的基本事件 (events),其基本事件 wi 的概率為 pi, i=1,2,…,n。我們記之為 ![]() 。當然,我們有基本關係式
。當然,我們有基本關係式 ![]() , i=1,2,…,n。我們要定義一個函數 H 它的定義域是所有的樣本空間,它在樣本空間
, i=1,2,…,n。我們要定義一個函數 H 它的定義域是所有的樣本空間,它在樣本空間 ![]() 的值,我們用
的值,我們用 ![]() 來表示(X 省略掉)我們要拿這個數來刻劃具有概率分別為 p1,p2, …, pn 的事件 w1,w2,…,wn 的樣本空間的「不確定度」。
來表示(X 省略掉)我們要拿這個數來刻劃具有概率分別為 p1,p2, …, pn 的事件 w1,w2,…,wn 的樣本空間的「不確定度」。 ![]() 若要精確地反映試驗結果的不確定度,似乎必須滿足下列三個基本條件:
若要精確地反映試驗結果的不確定度,似乎必須滿足下列三個基本條件:
- (i) 對固定 n 來說,H 是 (p1,…,pn) 的連續函數:(這是數學上很基本的要求)
代替硬幣,讓我們來擲骰子。這骰子是個材料均勻各面光滑的正六邊體。當我們將它擲到桌面上時,每個面朝上的機率都是
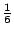 。究竟是那面朝上的不確定度,顯然比旋轉光滑對稱硬幣那面朝上的不確定度要大許多。這個事實若用 H 來表達,應當是
。究竟是那面朝上的不確定度,顯然比旋轉光滑對稱硬幣那面朝上的不確定度要大許多。這個事實若用 H 來表達,應當是  一般來說,H 應當滿足。
一般來說,H 應當滿足。 - (ii) 若
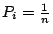 ,i=1,2,…,n,則對應的
,i=1,2,…,n,則對應的 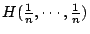 應當是 n 的單調遞增函數。
應當是 n 的單調遞增函數。 現在有一筆研究經費要分配給工程系的一名教授或數學系的兩名教授之一。假設工程系教授 A 獲得這筆經費的可能性是
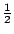 ,數學系教授 B 獲此經費的可能性為
,數學系教授 B 獲此經費的可能性為 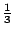 ,而數學系教授 C 獲此經費的可能性為
,而數學系教授 C 獲此經費的可能性為 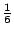 了。事實上,這筆經費現在在教務長那裡,他認為為了公平起見,工程系獲此資助的可能性為
了。事實上,這筆經費現在在教務長那裡,他認為為了公平起見,工程系獲此資助的可能性為 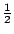 ,而數學系獲此資助的可能性亦為
,而數學系獲此資助的可能性亦為 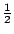 。工程系若獲此資助,系主任只會給教授 A,沒有其他的侯選人。但在數學系教授獲資助的前提下,教授 B 獲資助的可能性為
。工程系若獲此資助,系主任只會給教授 A,沒有其他的侯選人。但在數學系教授獲資助的前提下,教授 B 獲資助的可能性為 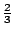 ,而教授 C 獲資助的可能性為
,而教授 C 獲資助的可能性為 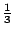 (見圖1-2),這兩種「絕對不確定」和「相對不確定」分析應給出同樣的結果,也就是說,教授 A,B,C 獲此研究費的不確定度,
(見圖1-2),這兩種「絕對不確定」和「相對不確定」分析應給出同樣的結果,也就是說,教授 A,B,C 獲此研究費的不確定度, 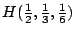 應當等於教務長將它分給工程系或數學系的不確定度,
應當等於教務長將它分給工程系或數學系的不確定度, 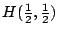 加上若是分到數學系,教授 B 或教授 C 得此資助的不確定度
加上若是分到數學系,教授 B 或教授 C 得此資助的不確定度 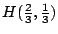 ,但這個不確定度是在此經費分到數學系的前提下。這種可能只有
,但這個不確定度是在此經費分到數學系的前提下。這種可能只有 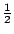 ,因此
,因此 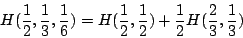

圖1-2
將此分析一般化,我們有下列的條件:
- (iii) 若某一試驗分解成多個相繼的試驗,則原先的 H 值應為相應的各個 H 值之加權和 (weighted sum)。
下面我們來證明一個重要結論:
- 定理1-1:
- 滿足條件(i)、(ii)和(iii)的函數 H 恰好具有形式
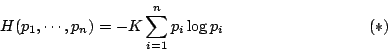
其中 K 為某個固定正常數。 - 證明:
- 我們分三步來證明此定理。
- 第一步:記
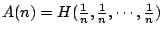 ,n 為正整數。
,n 為正整數。 - 斷言: A(sm)=mA(s),其中 s 和 m 均為正整數。
我們先對 s=2,m=3 用下列圖1-3所示來證明此斷言。即我們要證明

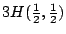 。由條件(iii)得
。由條件(iii)得
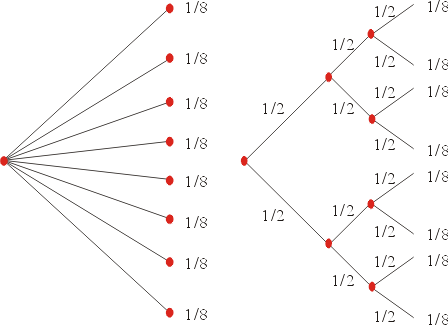
圖1-3
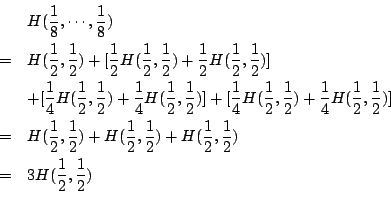
由歸納法易知,一般地有

這就證明了斷言。現在設正整數 t,s,n 和 m 滿足

兩邊取對數,則有
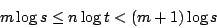
即
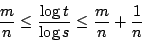
故有

由條件(ii),A 是其自變量的單調遞增函數,且由我們剛證的斷言,有
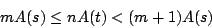
故有

由(1-1)和(1-2)式,我們得到
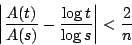
因為 n 可以取任意自然數,而上式左邊與 n 無關,故有
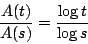
或
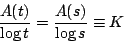
其中 K 為一固定正常數,這樣我們有
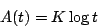
由此,
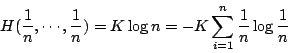
即,本定理對特殊情形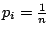 , i=1,…,n 成立。
, i=1,…,n 成立。 - 第二步:
現在對 pi 取一般的非有理數來證明此定理,我們對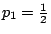 ,
,  ,
, 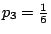 來描述證明的思想,作出下列圖1-4。
來描述證明的思想,作出下列圖1-4。
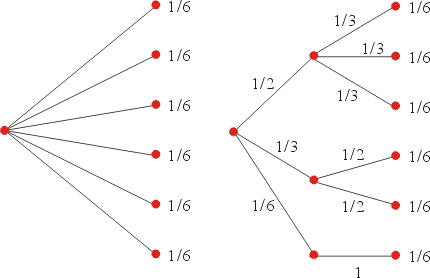
圖1-4
根據條件(iii)
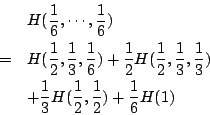
故有
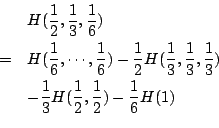
這樣分解的目的在於我們可用第一步證明的結果來證明第二步。令 n1=3, n2=2, n3=1,則
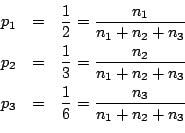
將上面結果抽象化,我們就有,
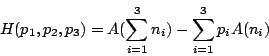
對一般情形,我們可依同法處理。設 p1,…,pr 為非負有理數,滿足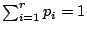 ,則存在自然數 n1,…,nr,使得
,則存在自然數 n1,…,nr,使得
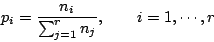
利用條件(iii),我們得到如下的等式
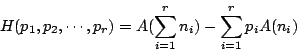
由第一步證明之結果,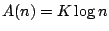 代入上式有
代入上式有
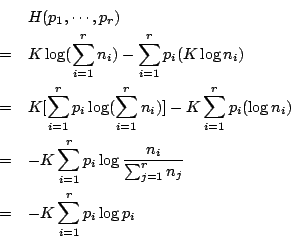
故我們證明了(*)式對任何滿足 的非負有理數 p1,…,pr 成立。
的非負有理數 p1,…,pr 成立。 - 第三步:設 p1,…,pr 為任意非負實數,
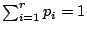 。由條件(i),H 為 p1,…,pr 的連續函數,而任何實數均可由有理數列來任意逼近,故第二步證明結果隱含了(*)式在實數情形之正確性。定理證畢。
。由條件(i),H 為 p1,…,pr 的連續函數,而任何實數均可由有理數列來任意逼近,故第二步證明結果隱含了(*)式在實數情形之正確性。定理證畢。
由定理中(*)式可知,若對某一個 i 有 pi=1,則 ![]() ,這正好和我們的願望相符:pi=1 意味著對應的事件總是發生的,因而不確定度為零。
,這正好和我們的願望相符:pi=1 意味著對應的事件總是發生的,因而不確定度為零。
因此,我們可以給出如下關於熵的定義,這個定義的熵 (entropy),又稱為 shannon 熵。
- 定義1-2:
- 由式
 定義的數,
定義的數, 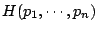 稱為對應於樣本空間
稱為對應於樣本空間  的熵。
的熵。
在本節之初,我們已知旋轉光滑硬幣時,正面朝上有 ![]() 的機率,反面朝上也有
的機率,反面朝上也有 ![]() 的機率,它的不確定度有最大。既然熵是關於不確定度的一種數學度量,這就自然地要求當
的機率,它的不確定度有最大。既然熵是關於不確定度的一種數學度量,這就自然地要求當 ![]() 時,H 給出最大值。要注意的是,我們在推導 H 表達式的三個基本條件中,並無強加此項要求。現在我們要證明:這個直觀的要求,事實上可由上述三個基本條件推出結論。
時,H 給出最大值。要注意的是,我們在推導 H 表達式的三個基本條件中,並無強加此項要求。現在我們要證明:這個直觀的要求,事實上可由上述三個基本條件推出結論。
- 命題1-3:
- 設
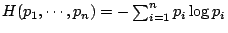 則
則
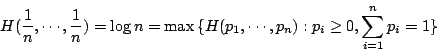
- 證明:
- 由初等微積分知函數
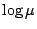 是 μ 的嚴格凹函數。任給
是 μ 的嚴格凹函數。任給 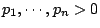 ,
, 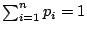 。
。
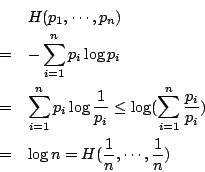
當某一 pi 為零時,比如說 pi=0。這就好像一個只有 n-1 個基本事件的樣本空間。由上面的推論
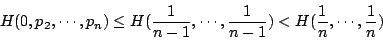
第二個不等號是由於條件(ii)。
這節定義的熵起源於信息理論的研究。是 C. Shannon 在1948年引進的。在此基礎上,蘇聯數學家 A.N. Kolmogorov 在1958年給出了動力系統熵的概念。從而揭開了現代遍歷理論研究的新篇章。
熵 (Entropy) (第 2 頁)
李天岩
首頁 | 搜尋
.原載於數學傳播十三卷三期
.作者當時任教於美國密西根州立大學數學系
‧對外搜尋關鍵字
2. Kolmogorov 熵
我們再來做旋轉光滑硬幣的遊戲。為了方便起見,我們稱硬幣的正面為 l,反面為 0。讓我們考察連續旋轉 n 次,其每次正反面出現的各種可能性。旋轉一次,有兩個可能性,或正面朝上,或反面朝上,即 1,0;旋轉兩次有 4=22 種可能性,即 11,10,01,00;一般來說,旋轉 n 次則有 2n 種可能性。把連續旋轉 n 次的任一可能結果看成一個「基本事件」,我們則得到一個具有 2n 個基本事件的樣本空間,其每一基本事件有同樣的概率 2-n。上節中所談 Shannon 熵給出了這個樣本空閒的不確定度──![]() 。現在我們要進一步問的是:如果我們已知旋轉硬幣第一次,第二次,… 第 n-1 次的結果,那麼第 n 次會是正面或會是反面的不確定度該是多少?
。現在我們要進一步問的是:如果我們已知旋轉硬幣第一次,第二次,… 第 n-1 次的結果,那麼第 n 次會是正面或會是反面的不確定度該是多少?
我們希望能用數學上的語言來描述這個問題。首先讓我們來考慮定義在 [0,1] 上的函數 ![]() ,也就是
,也就是
(見圖2-1),取 Lebesgue 測度 m 做為 [0,1] 上的測度,令
由此,我們則有
![/begin{displaymath} /bigvee_{i=0}^{n-1} f^{-1}(/overline{A}) =/{ [/frac{i-1}{2^n},/frac{i}{2^n}] : i=1,/cdots,2^n/} /end{displaymath}](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/img70.gif)
的劃分,這個劃分裡的每個區間
拿 n=3 其中的一個簡單情況來看。把 ![]() 這個區間左端的
這個區間左端的 ![]() 寫成
寫成
然後將
其中 ak=0 或 1, k=1,…,n。這個區間對應的是旋轉硬幣 n 次,出現
「已知旋轉硬幣第一次,第二次,…,第 n-1 次的結果,那麼第 n 次會是正面或反面的不確定度是多少?」的這一問題,拿 ![]() 和劃分
和劃分 ![]() 來描述,事實上是在問:已知 x,…,fn-1(x) 在劃分
來描述,事實上是在問:已知 x,…,fn-1(x) 在劃分 ![]() 裡的位置,那麼 fn(x) 會在
裡的位置,那麼 fn(x) 會在 ![]() 裡或在
裡或在 ![]() 裡的不確定度是多少呢?
裡的不確定度是多少呢?
讓我們來看 n=4 這個特殊情形。比如說我們已知前三次的結果,它們是 101(第一次正面,第二次反面,第三次正面),這在 ![]() 中所對應的區間是
中所對應的區間是 ![]() ,因為
,因為
仔細的看,這個間區事實上是,
元素x在這交集所代表的意義是:
已知 ![]() 在那裡,問 fn(x) 在那裡的不確定度,當 n 趨近於無窮大時的變化就是我們在這一節要談的 Kolmogorov 熵。
在那裡,問 fn(x) 在那裡的不確定度,當 n 趨近於無窮大時的變化就是我們在這一節要談的 Kolmogorov 熵。
我們將把我們的著眼點放在一般的概率測度空間 (Probability measure space) 和定義在它上面的可測變換 (measurable function)。設 ![]() 為一概率測度空間。即 X 為一集合, Σ 為 X 上的一些子集合所構成的一個
為一概率測度空間。即 X 為一集合, Σ 為 X 上的一些子集合所構成的一個 ![]() 代數, μ 為 Σ 上的概率測度,也就是說
代數, μ 為 Σ 上的概率測度,也就是說 ![]() 。假設
。假設 ![]() 為一個可測變換。這是指,Σ 中每個元素的逆像 f-1(A) 仍在 σ 中。我們任取 X 的一個有限劃分 (finite partition)
為一個可測變換。這是指,Σ 中每個元素的逆像 f-1(A) 仍在 σ 中。我們任取 X 的一個有限劃分 (finite partition) ![]() ,Am} 即
,Am} 即 ![]() 中每個集合 Ai 屬於 Σ,它們之間互不相交(交集的測度為 0)且聯集恰為 X。這樣
中每個集合 Ai 屬於 Σ,它們之間互不相交(交集的測度為 0)且聯集恰為 X。這樣 ![]() 可看成具有「基本事件」 A1,A2,…,Am 且有概率分布
可看成具有「基本事件」 A1,A2,…,Am 且有概率分布 ![]() ,…,
,…,![]() 的一個有限樣本空間。這個樣本空間經常被稱為「試驗結果」。上節中談到,這個「試驗結果」的 Shannon 熵應為:
的一個有限樣本空間。這個樣本空間經常被稱為「試驗結果」。上節中談到,這個「試驗結果」的 Shannon 熵應為:
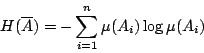
對給定的 f,集族
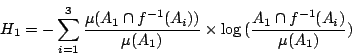
類似地,在
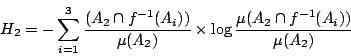
和

由推導 Shannon 熵定義的條件(ii)易知,在試驗結果
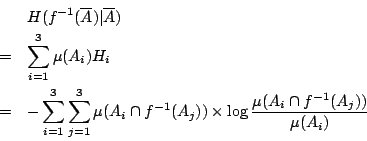
如法炮製,對一般的有限劃分
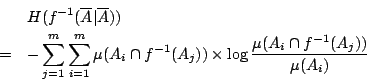
下面,我們來給出上述 ![]() 的另一等價型式以便後面推廣。
的另一等價型式以便後面推廣。
- 命題2-1:
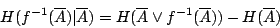
- 證明:
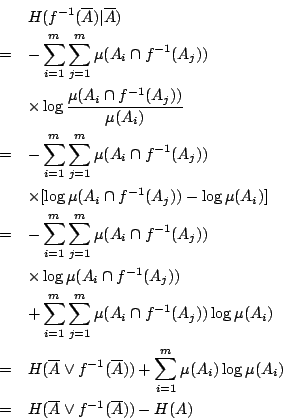
命題2-1在直觀上看也很顯然:試驗結果 ![]() 的不確定度
的不確定度 ![]() 應為試驗結果
應為試驗結果![]() 的不確定度
的不確定度 ![]() 在試驗結果
在試驗結果![]() 為已知條件下,試驗結果
為已知條件下,試驗結果 ![]() 的不確定度
的不確定度 ![]() 之和。
之和。
上述已知試驗結果![]() ,問試驗結果f-1(A)的不確定度,相當於已知x在
,問試驗結果f-1(A)的不確定度,相當於已知x在![]() 中的位置,我們問f(x)在
中的位置,我們問f(x)在![]() 中的位置的不確定度。已知
中的位置的不確定度。已知 ![]() 在分劃
在分劃![]() 中的位置,問 fn(x) 在
中的位置,問 fn(x) 在 ![]() 中的位置的不確定度,則相當於已知試驗結果
中的位置的不確定度,則相當於已知試驗結果 ![]()
![]() ,問試驗結果
,問試驗結果 ![]() 的不確定度。 Kolomogorov 熵基本上是在刻劃這個不確定度在當 n 趨近於無窮大時的漸近性質。
的不確定度。 Kolomogorov 熵基本上是在刻劃這個不確定度在當 n 趨近於無窮大時的漸近性質。
任給自然數n, ![]() 和
和 ![]() 都是 X 的有限劃分。在已知試驗結果,
都是 X 的有限劃分。在已知試驗結果, ![]() 的條件下,試驗結果
的條件下,試驗結果 ![]() 的不確定度,實際上是劃分
的不確定度,實際上是劃分 ![]() 的條件 Shannon 熵,它是
的條件 Shannon 熵,它是
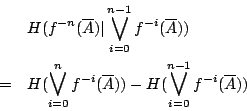
- 定義2-2:
- 設
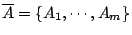 為 X的有限劃分,則可測變換
為 X的有限劃分,則可測變換  關於
關於 的熵定義為
的熵定義為
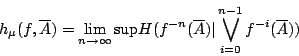
- 定義2-3:
- 設 (X,Σ,μ) 為一概率空間,
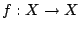 為一可測變換,則 f 的 Kolomogorov 熵定義為
為一可測變換,則 f 的 Kolomogorov 熵定義為
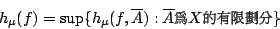
- 定義2-2:
- 設
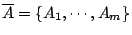 為 X 的有限劃分,則保測變換
為 X 的有限劃分,則保測變換 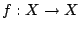 關於
關於 的熵定義為
的熵定義為
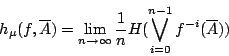
在證明此定義合理,且與定義2-2等價之前,我們首先注意到如下的事實:若f為保測變換,則 ![]() 這由條件
這由條件 ![]() 易見。若
易見。若![]() 和
和![]() 為X的兩個有限劃分,我們記
為X的兩個有限劃分,我們記 ![]() ,若
,若 ![]() 的每一元素是
的每一元素是![]() 中某些元素之聯(Union) (即
中某些元素之聯(Union) (即![]() 是
是![]() 的一個細分(refinement)) 我們需要下列引理,其證明稍後給出。
的一個細分(refinement)) 我們需要下列引理,其證明稍後給出。
- 引理2-4:
- 若
 ,則
,則 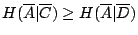
現在可以敘述並證明我們的等價定理了。
- 定理2-5:
- 若
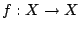 為保測變換,則對 X 的任一劃分
為保測變換,則對 X 的任一劃分 
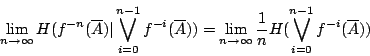
- 證明:
- n=1,則
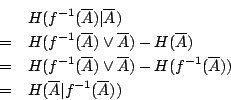
當 n=2 時,
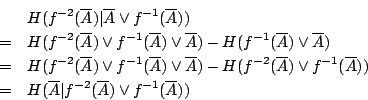
用歸納法易證,一般地有
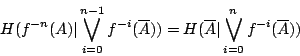
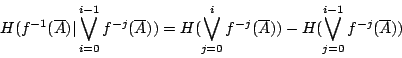
各式相加,我們有
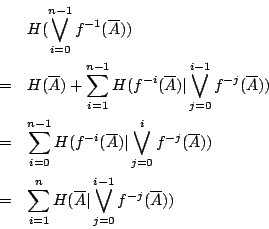
故有
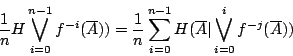
借用初等微積分的已知結果:

現在我們來證明引理2-4。
設 ![]() ,
, ![]() ,
, ![]() ,我們要證
,我們要證
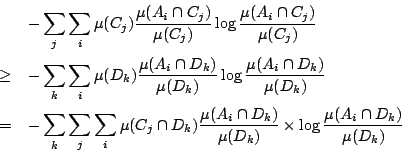
只須證明對每一 i 和 j

令
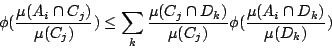
由於
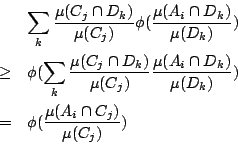
即我們證明了
歷史上,引進 Kolmogorov 熵概念的主要動力是關於概率空間保測變換之間共軛關係的不變量的研究。設 ![]() 和
和 ![]() 為兩個概率空間,
為兩個概率空間, ![]() 和
和 ![]() 為保測變換。我們說 T1 和 T2 共軛 (conjugate) 是指存在一個保測同構
為保測變換。我們說 T1 和 T2 共軛 (conjugate) 是指存在一個保測同構 ![]()
![]()
![]()
![]() 使得
使得 ![]() 。我們稱一個數量為共軛保測變換的「不變量 (invariance)」是指二個保測變換若是共軛,這個數量一定一樣。這個數量若不一樣,這兩個保測變換一定不共軛。共軛的保測變換具有同樣的遍歷性質。我們若能找到關於共軛保測變換的不變量,我們就可從本質上刻劃不同共軛類保測變換的特徵:Kolmogorov 熵就是這樣的一個重要的不變量。
。我們稱一個數量為共軛保測變換的「不變量 (invariance)」是指二個保測變換若是共軛,這個數量一定一樣。這個數量若不一樣,這兩個保測變換一定不共軛。共軛的保測變換具有同樣的遍歷性質。我們若能找到關於共軛保測變換的不變量,我們就可從本質上刻劃不同共軛類保測變換的特徵:Kolmogorov 熵就是這樣的一個重要的不變量。
早在1943年,人們就知道 Bernoulli 的 ( ![]() ) -雙邊移位算子 (two side shift) 和 (
) -雙邊移位算子 (two side shift) 和 ( ![]() )- 雙邊移位算子都具有可數個 Lebesgue 譜點,因而是譜同構的,但不知道它們是否共軛。直到1958年才由 Kolmogorov 證明了它們分別具有
)- 雙邊移位算子都具有可數個 Lebesgue 譜點,因而是譜同構的,但不知道它們是否共軛。直到1958年才由 Kolmogorov 證明了它們分別具有 ![]() 和
和 ![]() 的 Kolmogorov 熵,故非共軛。從而消除了遍歷理論這個重大懸念,並開創了一個嶄新的研究領域。我們這裡介紹的 Kolmogorov 熵的概念是由 Kolmogorov 的學生 Sinai 在1959年改進的,和 Kolmogorov 1958年給出的原始定義稍有不同。
的 Kolmogorov 熵,故非共軛。從而消除了遍歷理論這個重大懸念,並開創了一個嶄新的研究領域。我們這裡介紹的 Kolmogorov 熵的概念是由 Kolmogorov 的學生 Sinai 在1959年改進的,和 Kolmogorov 1958年給出的原始定義稍有不同。
熵 (Entropy) (第 3 頁)
李天岩
首頁 | 搜尋
.原載於數學傳播十三卷三期
.作者當時任教於美國密西根州立大學數學系
‧對外搜尋關鍵字
3. 拓樸熵 (Topological Entropy)
連續性是自然界的基本屬性之一。數學上連續的概念是由拓樸來刻劃的。拓樸空間 X 中由所有開集生成的 Borel 代數相當於測度空間裡的 ![]() 代數。拓樸空間上的連續映射相當於測度空間裡的可測變換。由此,我們可以將上節中所談的 Kolmogorov 熵在拓樸空間裡做相似性的定義,來描述連續映射的不確定性。在這過程中最大的困擾是:一般拓樸空間中,並沒有一個相似於測度空間裡的「測度」的度量。
代數。拓樸空間上的連續映射相當於測度空間裡的可測變換。由此,我們可以將上節中所談的 Kolmogorov 熵在拓樸空間裡做相似性的定義,來描述連續映射的不確定性。在這過程中最大的困擾是:一般拓樸空間中,並沒有一個相似於測度空間裡的「測度」的度量。
假設 X 為一個緊緻 (compact) Hausdorff 空間, ![]() 為一連續映射。由一般拓樸學知,存在有限開覆蓋 (finite open covering)。設
為一連續映射。由一般拓樸學知,存在有限開覆蓋 (finite open covering)。設 ![]() ,為 X 的一個有限開覆蓋,
,為 X 的一個有限開覆蓋,![]() 中能覆蓋 X 的子集族稱為
中能覆蓋 X 的子集族稱為 ![]() 中的子覆蓋 (subcover)。我們稱
中的子覆蓋 (subcover)。我們稱![]() 中的子覆蓋為「極小」(minimal),如果在
中的子覆蓋為「極小」(minimal),如果在 ![]() 中沒有一個比它元素少的子覆蓋。通常用
中沒有一個比它元素少的子覆蓋。通常用 ![]() 來代表
來代表![]() 中極小子覆蓋裡元素的個數。若把極小子覆蓋裡的每一個開集當做一個「基本事件」,大家的概率都是
中極小子覆蓋裡元素的個數。若把極小子覆蓋裡的每一個開集當做一個「基本事件」,大家的概率都是 ![]() ,我們則得到一個樣本空間。它的 Shannon 熵可以很輕易的算出,是
,我們則得到一個樣本空間。它的 Shannon 熵可以很輕易的算出,是 ![]() 。我們稱這個數目為開覆蓋
。我們稱這個數目為開覆蓋 ![]() 的熵,同時用符號 H(A) 來表示。
的熵,同時用符號 H(A) 來表示。
當 ![]() 為 X 上的開覆蓋時,
為 X 上的開覆蓋時, ![]() 也是一個開覆蓋。若
也是一個開覆蓋。若 ![]() 是
是 ![]() 的一個子覆蓋,但不一定是極小。所以,
的一個子覆蓋,但不一定是極小。所以,
若
我們還是用
- 定義3-1:
- 連續映射 f 關於有限覆蓋
 的拓樸熵 (topolgical entropy) 定義為:
的拓樸熵 (topolgical entropy) 定義為:
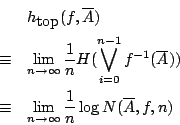
- 定義3-2:
- 緊緻 Hausdorff 拓樸空間 X 上的連續映射 f 的拓樸熵為
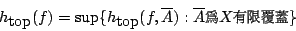
要使上述關於拓樸熵的定義合理,我們必須證明定義3-1中的極限的存在。為此我們求助於下列仍然是初等微積分的結果。
- 引理3-3:
- 設實數序列
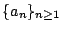 滿足條件
滿足條件  ,
, 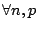 ,則
,則 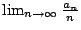 存在且等於
存在且等於 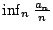 。
。 - 證明:
- 固定p > 0,每個n>0可寫成n=kp+i,其中
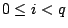 ,則
,則

當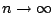 時
時 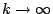 ,故有
,故有

因此,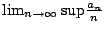
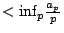 另一方面,從不等式
另一方面,從不等式
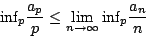
可知,極限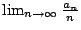 存在且等於
存在且等於  可知,極限
可知,極限 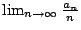 存在且等於
存在且等於 
- 定理3-4:
- 設 X 為緊緻 Hausdorff 空間,
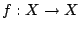 連續。任給 X 的有限開覆蓋
連續。任給 X 的有限開覆蓋  ,極限
,極限
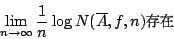
- 證明:
- 由定義知,
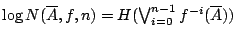 ,我們令其為 an。由(3-1),(3-2)可知
,我們令其為 an。由(3-1),(3-2)可知
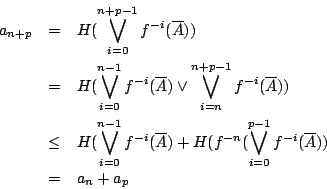
定理由結論恰由引理3-3推導。
拓樸嫡是由 R. Adler, A. Konhein 及 M. McAndrew 在1965年引進的,它是為了研究關於拓樸共軛不變量應運而生的。拓樸共軛的定義可如下給出。
- 定義3-5:
- 設
 和
和 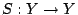 分別為緊緻拓樸空間 X 和 Y 上的連續映射。若存在同胚 (homeomorphism)
分別為緊緻拓樸空間 X 和 Y 上的連續映射。若存在同胚 (homeomorphism)  使得
使得 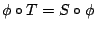 ,則稱拓樸共軛 (topologically conjugate) 於 S。這時,
,則稱拓樸共軛 (topologically conjugate) 於 S。這時, 就稱為一個共軛。
就稱為一個共軛。
我們可以證明,拓樸熵是拓樸共軛性的一個不變量。也就是說,兩個拓樸共軛的連續映射有相同的拓樸熵,反之亦然。事實上兩個拓樸共軛的連續映射在本質上給出相同的遍歷性質,因此,拓樸熵數學地刻劃了不同共軛類的拓樸動力系統 (Topological dynamical system) 的性質。
我們已知拓樸空間 X 加上其全體開集張成的 Borel ![]() 代數 β 構成一個可測空間。
代數 β 構成一個可測空間。![]() ,而 β 上給定的任何一個概率測度 μ 就構成一個概率測度空間
,而 β 上給定的任何一個概率測度 μ 就構成一個概率測度空間 ![]() 。 X 上的任一連續映射 f 同時也為
。 X 上的任一連續映射 f 同時也為 ![]() 上的可測變換,因而就有一個 Kolmogorov 熵隨之確定。另一方面,Borel 代數 β 上存在著眾多不同的概率測度,這樣就有了對應於不同概率測度的 Kolmogorov 熵組成的數集。然而,作為連續映射 f 的拓樸熵之定義與測度無關,它是唯一確定的。我們自然發出疑問:這兩種熵有何內在聯繫?既然拓樸嫡概念是由 Kolmogorov 熵概念衍生而來,我們有信心認為它們的確存在著情同手足的關係。這方面的結果多采多姿。比如說,
上的可測變換,因而就有一個 Kolmogorov 熵隨之確定。另一方面,Borel 代數 β 上存在著眾多不同的概率測度,這樣就有了對應於不同概率測度的 Kolmogorov 熵組成的數集。然而,作為連續映射 f 的拓樸熵之定義與測度無關,它是唯一確定的。我們自然發出疑問:這兩種熵有何內在聯繫?既然拓樸嫡概念是由 Kolmogorov 熵概念衍生而來,我們有信心認為它們的確存在著情同手足的關係。這方面的結果多采多姿。比如說,
- 定理3-8:
- 設 f 為緊緻拓樸空間 X 上的連續映射,則
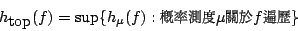
本節拓樸熵中,空間為緊緻的假設並非必要。 70年代初 Dinaburg 和 Bowen 分別給出了拓樸熵的等價定義。這些定義的優越性在於它們引導了一系列關於拓樸熵和測度熵(Kolmogorov 熵) 之間聯繫結果的證明。Bowen 的定義是對更廣泛的距離空間上一致連續映射族而言的。且導致了 n-環面上自同構拓樸熵公式的幾何證明。可惜,這位在遍歷理論研究中做出突出成就的數學家剛過而立之年就與世長辭了。
熵 (Entropy) (第 4 頁)
李天岩
首頁 | 搜尋
.原載於數學傳播十三卷三期
.作者當時任教於美國密西根州立大學數學系
‧對外搜尋關鍵字
4. Boltzmann 熵
熱力學中熵是一個極其重要的概念,最初由 Clausius 引進。後來 L. Boltzmann 在他發表在1866年關於氣體動力學理論的開創性工作中給出了熵的另一形式。這個熵在物理、化學的若干領域裡自始至終扮演著關鍵性的角色。可是 Boltzmann 熵和我們先前定義的 Kolmogorov 熵或拓樸熵並非一致。儘管如此,它們在數學的背景下,仍存在著千絲萬縷的聯繫。在這最後一節,我們將遨遊於 Boltzmann 熵的數學描述。
設 ![]() 為一有限樣本空間,則其 Shannon 熵為
為一有限樣本空間,則其 Shannon 熵為 ![]() ,現設
,現設 ![]() 為一測度空間。記 L'(X) 為定義在 X 上的 Lebesgue 可積函數全體。 L'(X) 中滿足等式
為一測度空間。記 L'(X) 為定義在 X 上的 Lebesgue 可積函數全體。 L'(X) 中滿足等式
的非負函數了 f(x) 稱為密度函數,其集合記為 D。易見等式
定義了
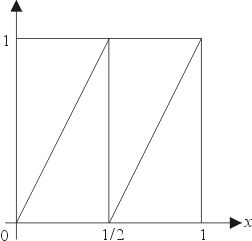
圖4-1
- 定義4-1:
- 設
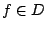 且
且 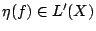 則 f 的 Boltzamann 熵定義為
則 f 的 Boltzamann 熵定義為

由 ![]() 定義知,
定義知, ![]() ,
, ![]() 。因而η是
。因而η是![]() 上的嚴格遞增凹函數,由Taylor展式,任給
上的嚴格遞增凹函數,由Taylor展式,任給![]() ,
,
 (1) <
(1) < 即,
簡化之,我們便有有名的 Gibbs 不等式,
任給函數
由於
在有限的樣本空間 (X,p1,…,pn) 中,Shannon 熵在 p1=p2= … =pn=n 時為最大,Boltzmann 熵在概率測度空間裡也有類似的性質。
- 命題4-2:
- 設
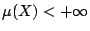 ,則密度函數
,則密度函數 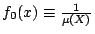 滿足
滿足
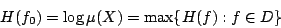
- 證明:
- 首先易見
 。其次,任給
。其次,任給 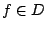 ,由不等式(4-1)
,由不等式(4-1)
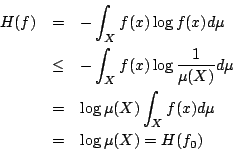
為了描述一些與Boltzmann熵有關的條件極值問題。我們引進一些概率論常用的術語。設X為一個隨機變量(Random Variable) ,即X為某一固定樣本空間上的可測實函數。 f(x)為這個測度空間的密度函數,則
稱為 X 的期望值 (Expected Value 或 Expectation)。而數
則稱為 X 的變異數 (variance)。期望值是關於於隨機變量 X 平均值的一個度量,變異數則表示隨機變量偏離其平均值的程度。下列性質,可以輕易的被驗證:
- (i)

- (ii)
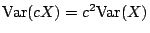
- (iii)

- (iv) 若 X 和 Y「獨立(independent)」則
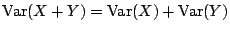
設有一列獨立隨機變量 ![]() ,
, ![]() ,
, ![]() ,令
,令
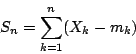
則,
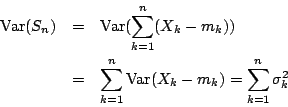
我們標準化 Sn,即令
則
概率理論中有個非常重要的基本定理:中央極限定理 (central limit theorem)。它大概的意思是說,在漸近狀態下,通常隨機變量 Tn 的概率分佈 (Probability distribution) 是遵循 Gauss 分佈規律的,也就是說,
其中 P 為樣本空間的概率分佈。
但是,為什麼大家都遵循的是 Gauss 分佈規律,而不是其他的分佈規律呢?事實上,這和熱力學第二定律有異曲同工之妙。熱力學第二定律大致上說,自然界的規律是,一切動態系統都是在向「熵」高的方向發展。從這個角度來看,在 ![]() ,
, ![]() 的條件下, Gauss 分佈的確有最大的 Boltzmann 熵,我們用下面的命題,對這點略加說明。
的條件下, Gauss 分佈的確有最大的 Boltzmann 熵,我們用下面的命題,對這點略加說明。
記 ![]()
- 命題4-3
- 設
 ,則
,則 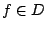 且
且
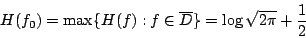
- 證明:
- 由公式
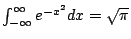 ,易知
,易知 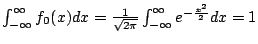 即
即  ,又由部分積分法易證
,又由部分積分法易證
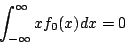
以及
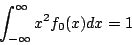
則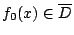 ,由不等式(4-1)
,由不等式(4-1)
![/begin{eqnarray*} H(f) &= & /int_{-/infty}^{/infty} f(x) /log{f(x)}dx// &/leq&... ...sqrt{2/pi}} ]dx // &=& /log{(/sqrt{2/pi})}+/frac{1}{2} = H(f_0) /end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/img274.gif)
類似地,記 ![]() 比照上述證明,我們有
比照上述證明,我們有
- 命題4-4:
- 設
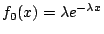 ,則
,則 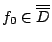 ,且
,且
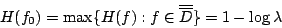
上述兩命題,可推廣到下述一般情形。設 ![]() ,給定約束
,給定約束
則H(f)在此約束下,最大值的密度函數應為
其中r為一常數。同樣,若有兩個約束
和
則密度函數
給出了H(f)在這兩個約束下的最大值H(f0),其中r1,r2為兩常數。更一般地,我們有
- 命題4-4:
- 設
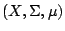 為一測度空間,非負函數
為一測度空間,非負函數 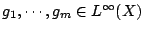 及正常數 r1,…,rm 滿足條件
及正常數 r1,…,rm 滿足條件

則 H(f) 在約束
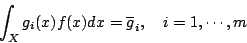
下最大密度值函數為
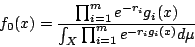
- 證明:
- 為簡單起見,令
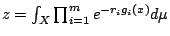 ,則
,則 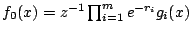 。不難算出
。不難算出
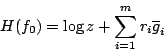
任給密度函數 f 滿足上述約束條件,由不等式(4-1)知,
![/begin{eqnarray*} H(f) &/leq& -/int_X f(x) /log{[z^{-1} /prod_{i=1}^{m} e^{-r_ig... ...] d/mu // &=& /log{z} + /sum_{i=1}^{m} r_i/overline{g}_i=H(f_0) /end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/img292.gif)
特別,當 m=1 時,若 g(x) 看成是系統的能量時, f0(x)= z-1 e-rg(x) 恰好就是 Gibbs 典型分怖函數,且 ![]() 為其分析函數,而對應的最大熵
為其分析函數,而對應的最大熵 ![]() 恰好就是眾所周知的熱力學熵。
恰好就是眾所周知的熱力學熵。
- 熵 (Entropy)
- 熵 (Entropy)
- 熵-entropy
- 信息熵 information Entropy
- 什么是熵(Entropy)?
- 信息熵(Information Entropy)
- 什么是熵(Entropy)?
- 什么是熵(Entropy)?
- 熵(entropy)
- 信息熵(entropy)
- Cross-Entropy 交叉熵
- 熵编码(entropy encoder)
- Entropy
- Entropy
- Entropy
- Entropy
- 什么是熵 (Entropy)----第一部分
- 内核熵池entropy pool
- 碎谈嵌入式学习要点
- C#基础学习日志===>二维数组<===
- C#基础学习日志===>二维数组<===
- 程序员保持身心健康的八种方式
- 毕生收集的一些卫星电视的地址
- 熵 (Entropy)
- linux面试题参考答案(转)
- HashTab 2.08 简体中文版
- 人生格言精选
- Linux的几个概念
- C#委托及事件
- 期末作业
- Fedora 8平台Mysql 5的安装
- 我Faint--ICMP的校验


