hdu 1619 Unidirectional TSP【记忆化dp】
来源:互联网 发布:三星s7检查网络连接 编辑:程序博客网 时间:2024/06/03 18:49
Unidirectional TSP
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 476 Accepted Submission(s): 235
Problem Description
Problems that require minimum paths through some domain appear in many different areas of computer science. For example, one of the constraints in VLSI routing problems is minimizing wire length. The Traveling Salesperson Problem (TSP) -- finding whether all the cities in a salesperson's route can be visited exactly once with a specified limit on travel time -- is one of the canonical examples of an NP-complete problem; solutions appear to require an inordinate amount of time to generate, but are simple to check.
This problem deals with finding a minimal path through a grid of points while traveling only from left to right.
Given an m*n matrix of integers, you are to write a program that computes a path of minimal weight. A path starts anywhere in column 1 (the first column) and consists of a sequence of steps terminating in column n (the last column). A step consists of traveling from column i to column i+1 in an adjacent (horizontal or diagonal) row. The first and last rows (rows 1 and m) of a matrix are considered adjacent, i.e., the matrix ``wraps'' so that it represents a horizontal cylinder. Legal steps are illustrated below.
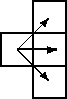
The weight of a path is the sum of the integers in each of the n cells of the matrix that are visited.
For example, two slightly different 5*6 matrices are shown below (the only difference is the numbers in the bottom row).
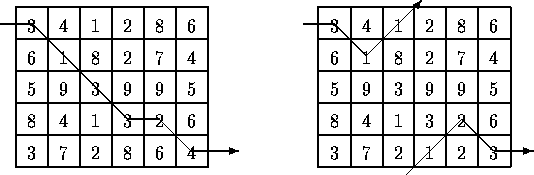
The minimal path is illustrated for each matrix. Note that the path for the matrix on the right takes advantage of the adjacency property of the first and last rows.
This problem deals with finding a minimal path through a grid of points while traveling only from left to right.
Given an m*n matrix of integers, you are to write a program that computes a path of minimal weight. A path starts anywhere in column 1 (the first column) and consists of a sequence of steps terminating in column n (the last column). A step consists of traveling from column i to column i+1 in an adjacent (horizontal or diagonal) row. The first and last rows (rows 1 and m) of a matrix are considered adjacent, i.e., the matrix ``wraps'' so that it represents a horizontal cylinder. Legal steps are illustrated below.

The weight of a path is the sum of the integers in each of the n cells of the matrix that are visited.
For example, two slightly different 5*6 matrices are shown below (the only difference is the numbers in the bottom row).

The minimal path is illustrated for each matrix. Note that the path for the matrix on the right takes advantage of the adjacency property of the first and last rows.
Input
The input consists of a sequence of matrix specifications. Each matrix specification consists of the row and column dimensions in that order on a line followed by integers where m is the row dimension and n is the column dimension. The integers appear in the input in row major order, i.e., the first n integers constitute the first row of the matrix, the second n integers constitute the second row and so on. The integers on a line will be separated from other integers by one or more spaces. Note: integers are not restricted to being positive. There will be one or more matrix specifications in an input file. Input is terminated by end-of-file.
For each specification the number of rows will be between 1 and 10 inclusive; the number of columns will be between 1 and 100 inclusive. No path's weight will exceed integer values representable using 30 bits
For each specification the number of rows will be between 1 and 10 inclusive; the number of columns will be between 1 and 100 inclusive. No path's weight will exceed integer values representable using 30 bits
Output
Two lines should be output for each matrix specification in the input file, the first line represents a minimal-weight path, and the second line is the cost of a minimal path. The path consists of a sequence of n integers (separated by one or more spaces) representing the rows that constitute the minimal path. If there is more than one path of minimal weight the path that is lexicographically smallest should be output.
Sample Input
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 8 6 4
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 1 2 3
2 2
9 10 9 10
Sample Output
1 2 3 4 4 5
16
1 2 1 5 4 5
11
1 1
19
Sample Input
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 8 6 4
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 1 2 3
2 2
9 10 9 10
Sample Output
1 2 3 4 4 5
16
1 2 1 5 4 5
11
1 1
19
Source
UVA
思路:因为图还是相对而言不小的一个图,直接dfs是一定会超时的,分析题目,对于同一个点,很多走法都会走到这一个点,所以我们可以采用记忆化搜索的方法来优化算法。对于每一个已经dfs过的点的值进行记录、因为一共就有三种走法,所以状态转移方程也并不难推出:
dp【i】【j】=a【i】【j】+min(dp【i-1】【j+1】,dp【i】【j+1】,dp【i+1】【j+1】);
对于起点的确定,我们可以枚举一遍,对于终点,我们是不用多考虑的,因为在记忆化搜索的过程中就得到了最小值,然后我们维护这个最小值,并且最终确定起点。
我们拿样例1说话,dp之后对于dp数组内数据是这样的(已知起点是1,0):
16 15 13 12 12 6
0 13 20 13 11 4
0 0 12 15 13 5
0 0 10 9 6 6
0 17 11 14 10 4
不难发现,我们每一次走的点都是相对上一个点能走的三个位子里边dp值最小的那个点。
(1,1)--------->(2,2)--------->(3,3)--------->(4,4)--------->(4,5)--------->(6,6)
所以根据这样的思路,我们对应写出代码。因为我的代码写的有点挫,我们分块来研究。
首先是记忆化搜索部分:
ll dfs(int x,int y){ if(y>=m)return 0;//控制范围 //printf("%d %d\n",x,y); if(dp[x][y]==0)//如果这个点没有走过,我们走一下 { ll a,b,c; if(x-1>=0)//记得第一行和最后一行是相连的 a=dfs(x-1,y+1); else a=dfs(n-1,y+1); b=dfs(x,y+1); if(x+1<n) c=dfs(x+1,y+1); else c=dfs(0,y+1); dp[x][y]=aa[x][y]+min(a,min(b,c));//状态转移方程 return dp[x][y]; } else return dp[x][y];//如果这个点已经走过了,直接return dp的值。}其次是对于枚举起点和初始化的部分:int main(){ while(scanf("%d%d",&n,&m)!=EOF) { for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { scanf("%I64d",&aa[i][j]); } } int pos; ll ans=0x3f3f3f; for(int i=0;i<n;i++)//枚举第一列上边全部的起点 { memset(dp,0,sizeof(dp));//每一次对应情况都不同,都应该清空dp数组 dfs(i,0); if(dp[i][0]<ans){ans=dp[i][0];pos=i;}//维护最小值 } memset(dp,0,sizeof(dp)); dfs(pos,0); dfs2(pos,0);//这次深搜是用来输出路径的 printf("%I64d\n",ans); }}最后是对于输出路径部分的控制。需要格外注意的一个点是如果当前点能走到的三个地方的值有相同的部分,那么要输出行号相对小的。
void dfs2(int x,int y){ if(y>=m)return ; if(y!=m-1) printf("%d ",x+1); else printf("%d\n",x+1);//注意控制输出格式 ll a,b,c; int rowa,rowb,rowc; if(x-1>=0){a=dp[x-1][y+1];rowa=x-1;}//对于每一种能够走到的位子进行枚举 else {a=dp[n-1][y+1];rowa=n-1;} b=dp[x][y+1];rowb=x; if(x+1<n){c=dp[x+1][y+1];rowc=x+1;} else {c=dp[0][y+1];rowc=0;} if(a==b&&b==c)//如果有值相同的情况,进行下一层深搜的时候要行号尽量小 { dfs2(min(rowa,min(rowb,rowc)),y+1); } else if(a==b&&a<c) { dfs2(min(rowa,rowb),y+1); } else if(a==c&&a<b) { dfs2(min(rowa,rowc),y+1); } else if(b==c&&b<a) { dfs2(min(rowb,rowc),y+1); } else//如果没有值相同的情况,直接走dp值小的那个点 { if(min(a,min(b,c))==a)dfs2(rowa,y+1); if(min(a,min(b,c))==b)dfs2(rowb,y+1); if(min(a,min(b,c))==c)dfs2(rowc,y+1); }}完整的AC代码:
#include<stdio.h>#include<string.h>#include<iostream>using namespace std;#define ll long long intll aa[225][225];ll dp[225][225];int n,m;ll min(ll a,ll b){ return a>b?b:a;}ll dfs(int x,int y){ if(y>=m)return 0; //printf("%d %d\n",x,y); if(dp[x][y]==0) { ll a,b,c; if(x-1>=0) a=dfs(x-1,y+1); else a=dfs(n-1,y+1); b=dfs(x,y+1); if(x+1<n) c=dfs(x+1,y+1); else c=dfs(0,y+1); dp[x][y]=aa[x][y]+min(a,min(b,c)); return dp[x][y]; } else return dp[x][y];}void dfs2(int x,int y){ if(y>=m)return ; //printf("%d %d\n",x+1,y+1); if(y!=m-1) printf("%d ",x+1); else printf("%d\n",x+1); ll a,b,c; int rowa,rowb,rowc; if(x-1>=0){a=dp[x-1][y+1];rowa=x-1;} else {a=dp[n-1][y+1];rowa=n-1;} b=dp[x][y+1];rowb=x; if(x+1<n){c=dp[x+1][y+1];rowc=x+1;} else {c=dp[0][y+1];rowc=0;} // printf("row:%d %d %d\n",rowa,rowb,rowc); //printf(" %I64d %I64d %I64d\n",a,b,c); if(a==b&&b==c) { //printf("%d %d %d\n",rowa,rowb,rowc); dfs2(min(rowa,min(rowb,rowc)),y+1); } else if(a==b&&a<c) { dfs2(min(rowa,rowb),y+1); } else if(a==c&&a<b) { dfs2(min(rowa,rowc),y+1); } else if(b==c&&b<a) { dfs2(min(rowb,rowc),y+1); } else { if(min(a,min(b,c))==a)dfs2(rowa,y+1); if(min(a,min(b,c))==b)dfs2(rowb,y+1); if(min(a,min(b,c))==c)dfs2(rowc,y+1); }}int main(){ while(scanf("%d%d",&n,&m)!=EOF) { for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { scanf("%I64d",&aa[i][j]); } } int pos; ll ans=0x3f3f3f; for(int i=0;i<n;i++) { memset(dp,0,sizeof(dp)); dfs(i,0); if(dp[i][0]<ans){ans=dp[i][0];pos=i;} } memset(dp,0,sizeof(dp)); dfs(pos,0); dfs2(pos,0); printf("%I64d\n",ans); }} 0 0
- hdu 1619 Unidirectional TSP【记忆化dp】
- hdu 1619 Unidirectional TSP 记忆化搜索
- HDU-1619 Unidirectional TSP dp
- hdu-1619 Unidirectional TSP(dp)
- 【DFS(记忆化)】hdu 1619 Unidirectional TSP
- HDU 1619 Unidirectional TSP (dp,dfs)
- HDU 1619 Unidirectional TSP(dp)
- UVA 116 Unidirectional TSP(DP+记忆化搜索)
- HDU-1619-Unidirectional TSP
- hdu 1619 单向TSP Unidirectional TSP
- uva116 - Unidirectional TSP(记忆化搜索)
- Unidirectional TSP(dp)
- HDU 1619:Unidirectional TSP【dfs & 回忆路径】
- dp uva-116-Unidirectional TSP
- UVa 116 Unidirectional TSP (DP)
- UVA 116 Unidirectional TSP (DP)
- UVa 116 - Unidirectional TSP(DP)
- UVA116 Unidirectional TSP easy DP
- 透视变换和仿射变换(下)
- RTP类型和时间戳
- 探讨kafka的分区数与多线程消费
- Python面向对象高级编程——学习笔记
- Scala进阶源码实战之八——隐式转换和隐式参数
- hdu 1619 Unidirectional TSP【记忆化dp】
- GitHub源代码管理基本操作
- 两人结队练习时的感受
- 直接选择排序
- angularjs初入
- 特征选择方法总结
- java学习笔记(3)多态
- Docker学习笔记
- python numpy使用


