poj 2409 Let it Bead（polya 定理）

来源：互联网发布：兰州知行学院官网编辑：程序博客网时间：2024/06/04 18:55

Let it Bead

Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 5387 Accepted: 3601

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

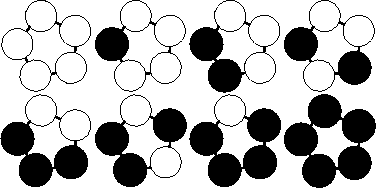For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 12 12 25 12 52 66 20 0

Sample Output

123581321

Source

Ulm Local 2000

[Submit] [Go Back] [Status] [Discuss]

题解: polya 定理

定理(Polya定理)：设G’是n个对象的一个置换群。

用m种颜色去对这n个对象进行染色，则不同的方案数为(在置换群G’的作用下变成相同的方案算是同一种方案)：

L=1/|G'|[m^c(a1')+...+m^c(ag')]

其中G’={a1’,…,ag’}，c(ai’)表示置换ai’的循环节数。

这个题给出颜色数和珠子的个数，让你求有多少不同的项链。

其实每一种项链的方式就是一个置换，注意这里的置换是位置的置换与颜色无关。但是这些置换中有很多都可以通过一些项链旋转或翻转的方式得到，那么我们需要计算的是不同等价类（所谓等价类就是对于一般的置换群G，k在G中置换的作用下的‘轨迹’形成一个封闭的集合，称为等价类，记为Ek。等价类之间可以互相转化。对于G= {(1)(2)(3)(4), (12), (34), (12)(34)}，显然有E1=E2={1,2}，E3=E4={3,4}。注意（12）表示的是置换中变换的是1、2，3,4与原序列保持不变，那么很显然e1,e3是相互独立的，因为无论怎么变化e1,e3都不可能相同。所以第一个和第三个不是等价类。）的个数。这道了polya定理，如何确定置换和置换的循环节呢？

如果s（表示珠子的个数）是奇数，则存在s种置换（对于这个环的题确定置换的个数就是确定对称轴数，这时只考虑翻转对称），每种置换包含s/2+1个循环（因为两边的数是两两对称，当前对称轴上的数单独属于一个循环节，所以是s/2+1）。

如果s是偶数，存在s/2种以边的中点为中心轴的翻转，每种包含s/2个循环（对称轴左右两两对称，另外还存在s/2种以点为中心的翻转，每种包含s/2+1个循环（对称轴上的两个数单独属于一个循环，其他的数两两对称）；

旋转：旋转i个珠子得到的循环数为gcd(i, s) ，一共可以旋转s 次

证明：设初始值为x，每次旋转i个珠子。有序列：x, x + i, x + i*2, ... , x + i*t

　　　假设x + i*t的时候回到原位置，即 x = (x + i*t)%n -> i*t%n = 0;

　　　也就是 t*i = 0(mod n)

　　解这个线性同余方程。

　　　d = gcd(n, i);

　　　i'x - n'y = 0/d;

　　　e = x*(0/d)%n = 0;

　　　解的剩余系：e, e + n/d, e + n/d*2 ... e+n/d*(d-1);

　　　发现解的剩余系中第一个有效的解为t = n/d = n/gcd(n, i);

　　　所以旋转i个珠子得到的循环长度为t = n/gcd(i, n),

　　　所以旋转i个珠子得到的循环数为n/t = gcd(i, n);　　　　

#include<iostream>#include<cstdio>#include<algorithm>#include<cstring>#define LL long long using namespace std;LL ans,n,m;LL gcd(LL x,LL y){LL r;while (y){r=x%y;x=y;y=r;}return x;}LL pow(LL num,LL x){LL base=num; LL ans=1;while (x){if (x&1)  ans=ans*base;x>>=1;base=base*base;}return ans;}int main(){while (scanf("%lld%lld",&n,&m)!=EOF){if (!n&&!m)  break;ans=0;for (LL i=1;i<=m;i++) ans+=pow(n,gcd(m,i));if (m%2)  ans+=pow(n,m/2+1)*m;else ans+=pow(n,m/2+1)*(m/2),     ans+=pow(n,m/2)*(m/2);printf("%lld\n",ans/(m*2));}}

0 0