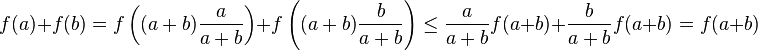维基百科中凸函数的定义 Convex function
来源:互联网 发布:南山空同 知乎 编辑:程序博客网 时间:2024/05/01 10:44


In mathematics, a real-valued function defined on an interval is called convex (or convex downward or concave upward) if the line segment between any two points on the graph of the function lies above or on the graph, in aEuclidean space (or more generally a vector space) of at least two dimensions. Equivalently, a function is convex if its epigraph (the set of points on or above the graph of the function) is a convex set. Well-known examples of convex functions include the quadratic function  and the exponential function
and the exponential function 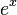 for any real number x.
for any real number x.
Convex functions play an important role in many areas of mathematics. They are especially important in the study of optimization problems where they are distinguished by a number of convenient properties. For instance, a (strictly) convex function on an open set has no more than one minimum. Even in infinite-dimensional spaces, under suitable additional hypotheses, convex functions continue to satisfy such properties and, as a result, they are the most well-understood functionals in the calculus of variations. In probability theory, a convex function applied to the expected value of a random variable is always less than or equal to the expected value of the convex function of the random variable. This result, known as Jensen's inequality, underlies many important inequalities (including, for instance, the arithmetic–geometric mean inequality and Hölder's inequality).
Exponential growth is a special case of convexity. Exponential growth narrowly means "increasing at a rateproportional to the current value", while convex growth generally means "increasing at an increasing rate (but not necessarily proportionally to current value)".
Contents
[hide]- 1Definition
- 2Properties
- 3Convex function calculus
- 4Strongly convex functions
- 4.1Uniformly convex functions
- 5Examples
- 6See also
- 7Notes
- 8References
- 9External links
Definition[edit]
Let  be a convex set in a real vector space and let f : X → R be a function.
be a convex set in a real vector space and let f : X → R be a function.
- f is called convex if:
- f is called strictly convex if:
- A function f is said to be (strictly) concave if −f is (strictly) convex.
Properties[edit]
1. Suppose f is a function of one real variable defined on an interval, and let
(note that R(x1, x2) is the slope of the purple line in the above drawing; note also that the function R is symmetric in x1, x2). f is convex if and only if R(x1, x2) is monotonically non-decreasing in x1, for any fixed x2 (or vice versa). This characterization of convexity is quite useful to prove the following results.
2. A convex function f defined on some open interval C is continuous on C and Lipschitz continuous on any closed subinterval. f admits left and right derivatives, and these are monotonically non-decreasing. As a consequence, f is differentiable at all but at most countably many points. If C is closed, then fmay fail to be continuous at the endpoints of C (an example is shown in the examples' section).
3. A function is midpoint convex on an interval C if
This condition is only slightly weaker than convexity. For example, a real valued Lebesgue measurable function that is midpoint convex will be convex bySierpinski Theorem.[1] In particular, a continuous function that is midpoint convex will be convex.
4. A differentiable function of one variable is convex on an interval if and only if its derivative is monotonically non-decreasing on that interval. If a function is differentiable and convex then it is also continuously differentiable. For the basic case of a differentiable function from (a subset of) the real numbers to the real numbers, "convex" is equivalent to "increasing at an increasing rate".
5. A continuously differentiable function of one variable is convex on an interval if and only if the function lies above all of its tangents:[2]:69
for all x and y in the interval. In particular, if f′(c) = 0, then c is a global minimum of f(x).
6. A twice differentiable function of one variable is convex on an interval if and only if its second derivative is non-negative there; this gives a practical test for convexity. Visually, a twice differentiable convex function "curves up", without any bends the other way (inflection points). If its second derivative is positive at all points then the function is strictly convex, but the converse does not hold. For example, the second derivative of f(x) = x4 is f ′′(x) = 12x2, which is zero for x = 0, but x4 is strictly convex.
More generally, a continuous, twice differentiable function of several variables is convex on a convex set if and only if its Hessian matrix is positive semidefinite on the interior of the convex set.
7. Any local minimum of a convex function is also a global minimum. A strictly convex function will have at most one global minimum.[3]
8. For a convex function f, the sublevel sets {x | f(x) < a} and {x | f(x) ≤ a} with a ∈ R are convex sets. However, a function whose sublevel sets are convex sets may fail to be a convex function. A function whose sublevel sets are convex is called a quasiconvex function.
9. Jensen's inequality applies to every convex function f. If X is a random variable taking values in the domain of f, then E(f(X)) ≥ f(E(X)). (Here E denotes themathematical expectation.)
10. If a function f is convex, and f(0) ≤ 0, then f is superadditive on the positive reals.
- Proof: Since f is convex, let y = 0, then:
- From this we have:
- Proof: Since f is convex, let y = 0, then:
Convex function calculus[edit]
- If f and g are convex functions, then so are
 and
and  , i.e. the set of convex functions on a given domain form a semifield.
, i.e. the set of convex functions on a given domain form a semifield. - If f and g are convex functions and g is non-decreasing, then
 is convex. As an example, if f(x) is convex, then so is
is convex. As an example, if f(x) is convex, then so is  , because
, because 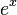 is convex and monotonically increasing.
is convex and monotonically increasing. - If f is concave and g is convex and non-increasing, then
 is convex.
is convex. - Convexity is invariant under affine maps: that is, if f is convex with domain
 , then so is
, then so is  , where
, where  with domain
with domain  .
. - If f(x, y) is convex in x then
 is convex in x provided
is convex in x provided  for some x, even if C is not convex.
for some x, even if C is not convex. - If f(x) is convex, then its perspective
 (whose domain is
(whose domain is  ) is convex.
) is convex. - The additive inverse of a convex function is a concave function.
- If
 is a convex real valued function, then
is a convex real valued function, then  for a countable collection of real numbers
for a countable collection of real numbers 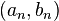
Strongly convex functions[edit]
The concept of strong convexity extends and parametrizes the notion of strict convexity. A strongly convex function is also strictly convex, but not vice versa.
A differentiable function f is called strongly convex with parameter m > 0 if the following inequality holds for all points x, y in its domain:[4]
or, more generally,
where  is any norm. Some authors, such as [5] refer to functions satisfying this inequality as elliptic functions.
is any norm. Some authors, such as [5] refer to functions satisfying this inequality as elliptic functions.
An equivalent condition is the following:[6]
It is not necessary for a function to be differentiable in order to be strongly convex. A third definition[6] for a strongly convex function, with parameter m, is that, for all x, y in the domain and ![t\in [0,1]](https://upload.wikimedia.org/math/d/9/a/d9a06fde4663cdd5b1ba693e9127232f.png) ,
,
Notice that this definition approaches the definition for strict convexity as m → 0, and is identical to the definition of a convex function when m = 0. Despite this, functions exist that are strictly convex but are not strongly convex for any m > 0 (see example below).
If the function f is twice continuously differentiable, then f is strongly convex with parameter m if and only if  for all x in the domain, whereI is the identity and
for all x in the domain, whereI is the identity and  is the Hessian matrix, and the inequality
is the Hessian matrix, and the inequality 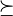 means that
means that  is positive semi-definite. This is equivalent to requiring that the minimum eigenvalue of
is positive semi-definite. This is equivalent to requiring that the minimum eigenvalue of  be at least m for all x. If the domain is just the real line, then
be at least m for all x. If the domain is just the real line, then  is just the second derivative
is just the second derivative  , so the condition becomes
, so the condition becomes  . If m = 0, then this means the Hessian is positive semidefinite (or if the domain is the real line, it means that
. If m = 0, then this means the Hessian is positive semidefinite (or if the domain is the real line, it means that  ), which implies the function is convex, and perhaps strictly convex, but not strongly convex.
), which implies the function is convex, and perhaps strictly convex, but not strongly convex.
Assuming still that the function is twice continuously differentiable, one can show that the lower bound of  implies that it is strongly convex. Start by using Taylor's Theorem:
implies that it is strongly convex. Start by using Taylor's Theorem:
for some (unknown) ![z \in \{ t x + (1-t) y : t \in [0,1] \}](https://upload.wikimedia.org/math/c/6/0/c603edbcc6e64bcb6e8f3564d1f9af57.png) . Then
. Then
by the assumption about the eigenvalues, and hence we recover the second strong convexity equation above.
A function f is strongly convex with parameter m if and only if the function 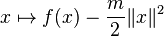 is convex.
is convex.
The distinction between convex, strictly convex, and strongly convex can be subtle at first glimpse. If f is twice continuously differentiable and the domain is the real line, then we can characterize it as follows:
- f convex if and only if
 for all x.
for all x. - f strictly convex if
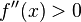 for all x (note: this is sufficient, but not necessary).
for all x (note: this is sufficient, but not necessary). - f strongly convex if and only if
 for all x.
for all x.
For example, consider a function f that is strictly convex, and suppose there is a sequence of points  such that
such that  . Even though
. Even though  the function is not strongly convex because
the function is not strongly convex because  will become arbitrarily small.
will become arbitrarily small.
A twice continuously differentiable function f on a compact domain  that satisfies
that satisfies 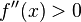 for all
for all  is strongly convex. The proof of this statement follows from the extreme value theorem, which states that a continuous function on a compact set has a maximum and minimum.
is strongly convex. The proof of this statement follows from the extreme value theorem, which states that a continuous function on a compact set has a maximum and minimum.
Strongly convex functions are in general easier to work with than convex or strictly convex functions, since they are a smaller class. Like strictly convex functions, strongly convex functions have unique minima on compact sets.
Uniformly convex functions[edit]
A uniformly convex function,[7][8] with modulus  , is a function f that, for all x, y in the domain and t ∈ [0, 1], satisfies
, is a function f that, for all x, y in the domain and t ∈ [0, 1], satisfies
where  is a function that is increasing and vanishes only at 0. This is a generalization of the concept of strongly convex function; by taking
is a function that is increasing and vanishes only at 0. This is a generalization of the concept of strongly convex function; by taking  we recover the definition of strong convexity.
we recover the definition of strong convexity.
Examples[edit]
- The function
 has
has  at all points, so f is a convex function. It is also strongly convex (and hence strictly convex too), with strong convexity constant 2.
at all points, so f is a convex function. It is also strongly convex (and hence strictly convex too), with strong convexity constant 2. - The function
 has
has  , so f is a convex function. It is strictly convex, even though the second derivative is not strictly positive at all points. It is not strongly convex.
, so f is a convex function. It is strictly convex, even though the second derivative is not strictly positive at all points. It is not strongly convex. - The absolute value function
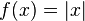 is convex (as reflected in the triangle inequality), even though it does not have a derivative at the point x = 0. It is not strictly convex.
is convex (as reflected in the triangle inequality), even though it does not have a derivative at the point x = 0. It is not strictly convex. - The function
 for 1 ≤ p is convex.
for 1 ≤ p is convex. - The exponential function
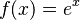 is convex. It is also strictly convex, since
is convex. It is also strictly convex, since  , but it is not strongly convex since the second derivative can be arbitrarily close to zero. More generally, the function
, but it is not strongly convex since the second derivative can be arbitrarily close to zero. More generally, the function  is logarithmically convex if fis a convex function. The term "superconvex" is sometimes used instead.[9]
is logarithmically convex if fis a convex function. The term "superconvex" is sometimes used instead.[9] - The function f with domain [0,1] defined by f(0) = f(1) = 1, f(x) = 0 for 0 < x < 1 is convex; it is continuous on the open interval (0, 1), but not continuous at 0 and 1.
- The function x3 has second derivative 6x; thus it is convex on the set where x ≥ 0 and concave on the set where x ≤ 0.
- The function
 on the domain of positive-definite matrices is convex.[2]:74
on the domain of positive-definite matrices is convex.[2]:74 - Every real-valued linear transformation is convex but not strictly convex, since if fis linear, then
 This statement also holds if we replace "convex" by "concave".
This statement also holds if we replace "convex" by "concave". - Every real-valued affine function, i.e., each function of the form
 , is simultaneously convex and concave.
, is simultaneously convex and concave. - Every norm is a convex function, by the triangle inequality and positive homogeneity.
- Examples of functions that are monotonically increasing but not convex include
 and g(x) = log(x).
and g(x) = log(x). - Examples of functions that are convex but not monotonically increasing include
 and
and  .
. - The function f(x) = 1/x has
 which is greater than 0 if x > 0, so f(x) is convex on the interval (0, +∞). It is concave on the interval (−∞, 0).
which is greater than 0 if x > 0, so f(x) is convex on the interval (0, +∞). It is concave on the interval (−∞, 0). - The function f(x) = x−2, with f(0) = +∞, is convex on the interval (0, +∞) and convex on the interval (-∞,0), but not convex on the interval (-∞, +∞), because of the singularity at x = 0.
See also[edit]
- Concave function
- Convex optimization
- Convex conjugate
- Geodesic convexity
- Kachurovskii's theorem, which relates convexity to monotonicity of the derivative
- Logarithmically convex function
- Pseudoconvex function
- Quasiconvex function
- Invex function
- Subderivative of a convex function
- Jensen's inequality
- Karamata's inequality
- Hermite–Hadamard inequality
- K-convex function
Notes[edit]
- Jump up^ Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press. p. 12. ISBN 9780122206504. Retrieved August 29, 2012.
- ^ Jump up to:a b Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 15, 2011.
- Jump up^ "If f is strictly convex in a convex set, show it has no more than 1 minimum". Math StackExchange. 21 Mar 2013. Retrieved 14 May 2016.
- Jump up^ Dimitri Bertsekas (2003). Convex Analysis and Optimization. Contributors: Angelia Nedic and Asuman E. Ozdaglar. Athena Scientific. p. 72. ISBN 9781886529458.
- Jump up^ Philippe G. Ciarlet (1989). Introduction to numerical linear algebra and optimisation. Cambridge University Press. ISBN 9780521339841.
- ^ Jump up to:a b Yurii Nesterov (2004). Introductory Lectures on Convex Optimization: A Basic Course. Kluwer Academic Publishers. pp. 63–64. ISBN 9781402075537.
- Jump up^ C. Zalinescu (2002). Convex Analysis in General Vector Spaces. World Scientific. ISBN 9812380671.
- Jump up^ H. Bauschke and P. L. Combettes (2011). Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer. p. 144. ISBN 978-1-4419-9467-7.
- Jump up^ Kingman, J. F. C. (1961). "A Convexity Property of Positive Matrices". The Quarterly Journal of Mathematics 12: 283–284. doi:10.1093/qmath/12.1.283.
References[edit]
- Bertsekas, Dimitri (2003). Convex Analysis and Optimization. Athena Scientific.
- Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.
- Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press.
- Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
- Krasnosel'skii M.A., Rutickii Ya.B. (1961). Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd.
- Lauritzen, Niels (2013). Undergraduate Convexity. World Scientific Publishing.
- Luenberger, David (1984). Linear and Nonlinear Programming. Addison-Wesley.
- Luenberger, David (1969). Optimization by Vector Space Methods. Wiley & Sons.
- Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
- Thomson, Brian (1994). Symmetric Properties of Real Functions. CRC Press.
- Zălinescu, C. (2002). Convex analysis in general vector spaces. River Edge, NJ: World Scientific Publishing Co., Inc. pp. xx+367. ISBN 981-238-067-1.MR 1921556.
External links[edit]
- Stephen Boyd and Lieven Vandenberghe, Convex Optimization (PDF)
- Hazewinkel, Michiel, ed. (2001), "Convex function (of a real variable)", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel, ed. (2001), "Convex function (of a complex variable)", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- 维基百科中凸函数的定义 Convex function
- 维基百科中凹函数的定义 Concave function
- 凸(Convex)函数定义
- 凸函数和凹函数在国内和国外的一些定义是相反的 Convex function和Concave Function
- 凹函数和凸函数,Concave Function和Convex Function
- 凸函数(convex)
- 042.Function 函数的定义
- 042.Function 函数的定义
- 百度百科 中对BI的定义
- JavaScript 中定义函数时用 var foo = function () {} 和 function foo() 的区别
- js function定义函数的方法
- 什么是 Convex function
- Concave and Convex Function
- VS开发】C中调用C++文件中定义的function函数
- Python function 函数定义
- ~function(){}()函数定义
- $(function(){})中定义变量的作用域
- [JavaScript] Script 中 function, variable 的定义会提升到函数执行前面;但是,function 中定义的 global variable 则不会被提升
- CocoPods的安装步骤
- 身份证号码生成
- SparkStreaming中Tanformations和状态管理
- 业务服务化给团队、技术带来的影响
- 浅谈Hibernate缓存机制:一级缓存、二级缓存
- 维基百科中凸函数的定义 Convex function
- 20160527 数据分析与SAS7 筛选数据集
- Java集合类详解
- SparkStreaming updateStateByKey 基本操作
- 百度定位+广播检测网络(小白版)
- 常用的字符串和数字之间的转换函数
- Android Fragment的标准写法
- SparkStreaming 实现广告计费系统中在线黑名单过滤实战
- 维基百科中凹函数的定义 Concave function
![\forall x_1, x_2 \in X, \forall t \in [0, 1]: \qquad f(tx_1+(1-t)x_2)\leq t f(x_1)+(1-t)f(x_2).](https://upload.wikimedia.org/math/7/8/d/78dc74f02d80babd3d6276a7ab18a809.png)

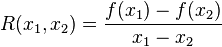


![f(tx) = f(tx+(1-t)\cdot 0) \le t f(x)+(1-t)f(0) \le t f(x), \quad \forall t \in[0,1].](https://upload.wikimedia.org/math/9/3/0/930ad6c1b088d1af333221211a92bc88.png)