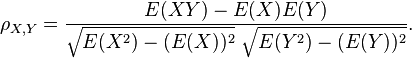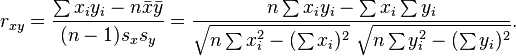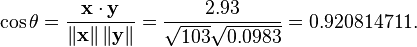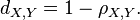皮尔逊相关系数
来源:互联网 发布:网络英语培训机构排名 编辑:程序博客网 时间:2024/06/05 22:29
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:
以上方程定义了总体相关系数, 一般表示成希腊字母ρ(rho)。基于样本对协方差和标准差进行估计,可以得到样本相关系数, 一般表示成r:
一种等价表达式的是表示成标准分的均值。基于(Xi, Yi)的样本点,样本皮尔逊系数是
其中
 、
、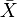 及
及 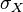
分别是标准分、样本平均值和样本标准差。
数学特性:
总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上(计算样本皮尔逊系数的情况),或者双变量分布完全在直线上(计算总体皮尔逊系数的情况),则相关系数等于1或-1。皮尔逊系数是对称的:corr(X,Y) = corr(Y,X)。
皮尔逊相关系数有一个重要的数学特性是,因两个变量的位置和尺度的变化并不会引起该系数的改变,即它该变化的不变量 (由符号确定)。也就是说,我们如果把X移动到a + bX和把Y移动到c + dY,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)。我们发现更一般的线性变换则会改变相关系数:参见之后章节对该特性应用的介绍。
由于μX = E(X), σX2 = E[(X ? E(X))2] = E(X2) ? E2(X),Y也类似, 并且
故相关系数也可以表示成
对于样本皮尔逊相关系数:
以上方程给出了计算样本皮尔逊相关系数简单的单流程算法,但是其依赖于涉及到的数据,有时它可能是数值不稳定的。
几何学的解释:
对于没有中心化的数据, 相关系数与两条可能的回归线y=gx(x) 和 x=gy(y) 夹角的余弦值一致。
对于中心化过的数据 (也就是说, 数据移动一个样本平均值以使其均值为0), 相关系数也可以被视作由两个随机变量 向量 夹角 的 余弦值(见下方)。
的 余弦值(见下方)。
一些人[谁?] 倾向于是用非中心化的相关系数 (non-Pearson-compliant) 。 比较如下。
例如,有5个国家的国民生产总值分别为 10, 20, 30, 50 和 80 亿美元。 假设这5个国家 (顺序相同) 的贫困百分比分别为 11%, 12%, 13%, 15%, and 18% 。 令 x 和 y 分别为包含上述5个数据的向量: x = (1, 2, 3, 5, 8) 和 y = (0.11, 0.12, 0.13, 0.15, 0.18)。
利用通常的方法计算两个向量之间的夹角  (参见 数量积), 未中心化 的相关系数是:
(参见 数量积), 未中心化 的相关系数是:
我们发现以上的数据特意选定为完全相关: y = 0.10 + 0.01 x。 于是,皮尔逊相关系数应该等于1。将数据中心化 (通过E(x) = 3.8移动 x 和通过 E(y) = 0.138 移动 y ) 得到 x = (?2.8, ?1.8, ?0.8, 1.2, 4.2) 和 y = (?0.028, ?0.018, ?0.008, 0.012, 0.042), 从中,

皮尔逊距离:
皮尔逊距离度量的是两个变量X和Y,它可以根据皮尔逊系数定义成
我们可以发现,皮尔逊系数落在 [-1, 1], 而皮尔逊距离落在 [0, 2]。
- Python实现:
- 使用的计算公式为:

frommathimportsqrtdefmultipl(a,b):sumofab=0.0foriinrange(len(a)):temp=a[i]*b[i]sumofab+=tempreturnsumofabdefcorrcoef(x,y):n=len(x)#求和sum1=sum(x)sum2=sum(y)#求乘积之和sumofxy=multipl(x,y)#求平方和sumofx2=sum([pow(i,2)foriinx])sumofy2=sum([pow(j,2)forjiny])num=sumofxy-(float(sum1)*float(sum2)/n)#计算皮尔逊相关系数den=sqrt((sumofx2-float(sum1**2)/n)*(sumofy2-float(sum2**2)/n))returnnum/denx=[0,1,0,3]y=[0,1,1,1]printcorrcoef(x,y)#0.471404520791
- 皮尔逊相关系数
- 皮尔逊相关系数
- 皮尔逊相关系数
- 皮尔逊相关系数
- 皮尔逊相关系数
- 皮尔逊相关系数理解
- 如何理解皮尔逊相关系数
- [算法1]皮尔逊相关系数
- Pearson Correlation 皮尔逊相关系数
- 皮尔逊相关系数公式
- 相关性学习-皮尔逊相关系数
- 皮尔逊相关系数JAVA实现
- 相关系数
- 相关系数
- 相关系数
- 相关系数
- 相关系数
- 相关系数
- Android集成支付宝步骤讲解
- XPath学习笔记
- Single Number II
- 2016-7
- Mybatis步步进阶(五)——Mybatis输入输出映射及动态SQL Review
- 皮尔逊相关系数
- python 字符编码处理
- Java千百问_06数据结构(023)_基本数据类型在内存中如何存放
- 跟我一起学Multiple View Geometry多视图几何(3)
- 【Django开发】阿里云服务器+apache+django部署你的网站
- 3-5:hidden过滤选择器
- LeetCode - 278. First Bad Version
- Because the people who are crazy enough to think they can change the world, are the ones who do.
- VS2013配置文件常见问题解决方法
![\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y},](http://upload.wikimedia.org/math/1/7/7/17709e96782a6a8bcd39904c5f2383e6.png)
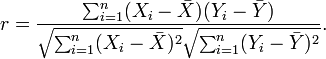

![E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y),\,](http://upload.wikimedia.org/math/d/6/8/d68b84931c79ab42b6a9374ffd5a4179.png)