协方差和马氏距离的理解
来源:互联网 发布:淘宝店铺如何运营方案 编辑:程序博客网 时间:2024/04/28 20:00
http://blog.csdn.net/lanbing510/article/details/8758651
整理了几篇看着不错的博客。
统计学的基本概念
方差:很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
为什么需要协方差?
上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。
协方差多了就是协方差矩阵
上一节提到的猥琐和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差那自然而然的我们会想到使用矩阵来组织这些数据。
关于协方差矩阵,下面是wiki上的介绍:
在统计学与概率论中,协方差矩阵(或称共变异矩阵)是一个矩阵,其每个元素是各个向量元素之间的方差。这是从标量随机变量到高维度随机向量的自然推广。
假设X是以n个标量随机变量组成的列向量,
并且μi 是其第i个元素的期望值, 即, μi = E(Xi)。协方差矩阵被定义的第i,j项是如下协方差:
即:
矩阵中的第(i,j)个元素是Xi与Xj的协方差。这个概念是对于标量随机变量方差的一般化推广。
尽管协方差矩阵很简单,可它却是很多领域里的非常有力的工具。它能导出一个变换矩阵,这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。(完整的证明请参考瑞利商)。 这个方法在统计学中被称为主成分分析(principal components analysis),在图像处理中称为Karhunen-Loève 变换(KL-变换)。
马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为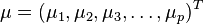 协方差矩阵为Σ的多变量向量
协方差矩阵为Σ的多变量向量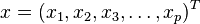 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量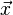 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧式距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离'.
其中σi

欧氏马氏距离的优劣
- 协方差和马氏距离的理解
- 协方差和马氏距离的理解
- 关于协方差和马氏距离的理解
- 关于协方差和马氏距离的理解
- 马氏距离与协方差矩阵
- 马氏距离与协方差矩阵
- 方差、协方差、马氏距离-总结
- 对协方差的理解
- 协方差的理解
- 协方差知识点的理解
- 马氏距离+协方差公式+无偏估计
- 协方差以及协方差矩阵的理解
- 期望、方差、协方差及相关系数的原理理解和计算
- 关于协方差矩阵的理解
- 关于协方差矩阵的理解
- 关于协方差矩阵的理解
- 对协方差矩阵的理解
- 关于协方差矩阵的理解
- 第三篇 设计模式之抽象工厂方法模式
- 怎样阅读一本书——让一本书真正属于你的方法之做笔记
- SAX解析xml文档
- java
- 达内学习笔记——MFC中Document创建过程
- 协方差和马氏距离的理解
- EventBus解释
- The requested resource is not available. 原因,成功解决
- android 传感器1--传感器list
- POJ3411-Paid Roads
- Windows7 安装MySQL5.7解压缩版及所遇到的问题与解决
- 共享内存
- 2016年KDD IJCAI WWW ICDM 文章的个人统计
- hduoj1212
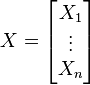

![马氏距离与协方差矩阵 \Sigma=\mathrm{E} \left[ \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right) \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right)^\top \right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png)
![马氏距离与协方差矩阵 = \begin{bmatrix} \mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \ \mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \ \vdots & \vdots & \ddots & \vdots \\ \ \mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)] \end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)





