角度计算

使用MPU6050硬件DMP解算姿态是非常简单的，下面介绍由三轴陀螺仪和加速度计的值来使用四元数软件解算姿态的方法。

我们先来看看如何用欧拉角描述一次平面旋转(坐标变换)：

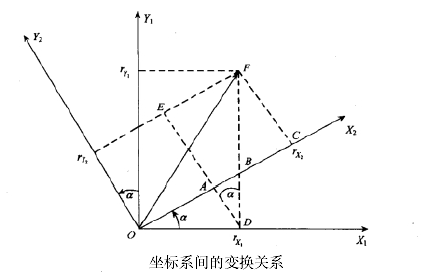
设坐标系绕旋转α角后得到坐标系,在空间中有一个矢量在坐标系中的投影为,在内的投影为由于旋转绕进行，所以Z坐标未变，即有。

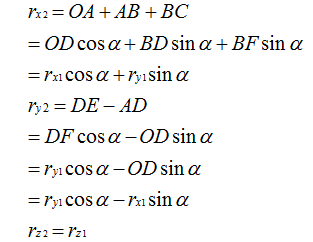
转换成矩阵形式表示为：

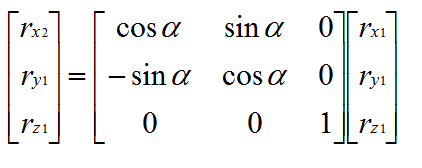
整理一下：

所以从旋转到可以写成

上面仅仅是绕一根轴的旋转，如果三维空间中的欧拉角旋转要转三次:

上面得到了一个表示旋转的方向余弦矩阵。

不过要想用欧拉角解算姿态，其实我们套用欧拉角微分方程就行了：

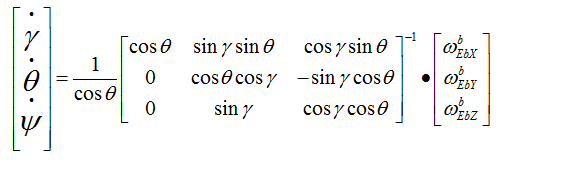
上式中左侧,,是本次更新后的欧拉角,对应row,pit,yaw。右侧，是上个周期测算出来的角度，，，三个角速度由直接安装在四轴飞行器的三轴陀螺仪在这个周期转动的角度，单位为弧度，计算间隔时T陀螺角速度，比如0.02秒0.01弧度/秒=0.0002弧度。间因此求解这个微分方程就能解算出当前的欧拉角。

前面介绍了什么是欧拉角，而且欧拉角微分方程解算姿态关系简单明了，概念直观容易理解，那么我们为什么不用欧拉角来表示旋转而要引入四元数呢？

一方面是因为欧拉角微分方程中包含了大量的三角运算，这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现神奇的“GimbalLock”。所以欧拉角方法只适用于水平姿态变化不大的情况，而不适用于全姿态飞行器的姿态确定。

四元数法只求解四个未知量的线性微分方程组，计算量小，易于操作，是比较实用的工程方法。

我们知道在平面(x,y)中的旋转可以用复数来表示，同样的三维中的旋转可以用单位四元数来描述。我们来定义一个四元数：

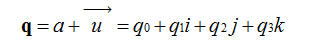
我们可以把它写成,其中,。那么是矢量，表示三维空间中的旋转轴。w是标量，表示旋转角度。那么就是绕轴旋转w度，所以一个四元数可以表示一个完整的旋转。只有单位四元数才可以表示旋转，至于为什么，因为这就是四元数表示旋转的约束条件。

而刚才用欧拉角描述的方向余弦矩阵用四元数描述则为：

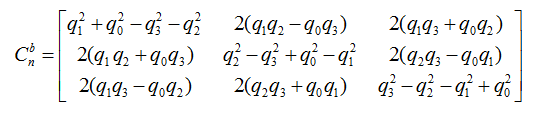
所以在软件解算中，我们要首先把加速度计采集到的值(三维向量)转化为单位向量,即向量除以模，传入参数是陀螺仪x,y,z值和加速度计x,y,z值：

<code>void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) { float norm; float vx, vy, vz; float ex, ey, ez;           norm = sqrt(ax*ax + ay*ay + az*az);       ax = ax / norm; ay = ay / norm; az = az / norm;  

下面把四元数换算成方向余弦中的第三行的三个元素。刚好vx,vy,vz 其实就是上一次的欧拉角（四元数）的机体坐标参考系换算出来的重力的单位向量。

<code>// estimated direction of gravity vx = 2*(q1*q3 - q0*q2); vy = 2*(q0*q1 + q2*q3); vz = q0*q0 - q1*q1 - q2*q2 + q3*q3; 

axyz是机体坐标参照系上，加速度计测出来的重力向量，也就是实际测出来的重力向量。

axyz是测量得到的重力向量，vxyz是陀螺积分后的姿态来推算出的重力向量，它们都是机体坐标参照系上的重力向量。

那它们之间的误差向量，就是陀螺积分后的姿态和加计测出来的姿态之间的误差。

向量间的误差，可以用向量叉积（也叫向量外积、叉乘）来表示，exyz就是两个重力向量的叉积。

这个叉积向量仍旧是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，正好拿来纠正陀螺。（你可以自己拿东西想象一下）由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。

<code>// integral error scaled integral gain exInt = exInt + ex*Ki; eyInt = eyInt + ey*Ki; ezInt = ezInt + ez*Ki; 

用叉积误差来做PI修正陀螺零偏

<code>// integral error scaled integral gain exInt = exInt + ex*Ki; eyInt = eyInt + ey*Ki; ezInt = ezInt + ez*Ki;  // adjusted gyroscope measurements gx = gx + Kp*ex + exInt; gy = gy + Kp*ey + eyInt; gz = gz + Kp*ez + ezInt; 

四元数微分方程，其中T为测量周期，为陀螺仪角速度，以下都是已知量，这里使用了一阶龙哥库塔求解四元数微分方程：

<code>// integrate quaternion rate and normalise q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT; q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT; q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT; q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;   

最后根据四元数方向余弦阵和欧拉角的转换关系，把四元数转换成欧拉角：

所以有：

Q_ANGLE.Yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yaw Q_ANGLE.Y  = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch Q_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll

笔者最近在做四轴，涉及到地磁计的融合算法，网上大多数是x-IMU的融合代码，但是这段代码对于地磁计的融合说明没有做过多的解释，网上没有相关讨论，仅在阿莫论坛看到一篇相关的代码解释，里面有关于地磁计融合部分的解说，个人觉得说的不是很清楚，虽然是正确的，我这里再补充啰嗦一下。

    首先给出x-IMU关于陀螺仪、加速度计、地磁计的融合代码：

[cpp] view plain copy print?

1. void MahonyAHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz) {  
2.     float recipNorm;  
3.     float q0q0, q0q1, q0q2, q0q3, q1q1, q1q2, q1q3, q2q2, q2q3, q3q3;    
4.     float hx, hy, bx, bz;  
5.     float halfvx, halfvy, halfvz, halfwx, halfwy, halfwz;  
6.     float halfex, halfey, halfez;  
7.     float qa, qb, qc;  
8.   
9.     // Use IMU algorithm if magnetometer measurement invalid (avoids NaN in magnetometer normalisation)  
10.     if((mx == 0.0f) && (my == 0.0f) && (mz == 0.0f)) {  
11.         MahonyAHRSupdateIMU(gx, gy, gz, ax, ay, az);  
12.         return;  
13.     }  
14.   
15.     // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)  
16.     if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) {  
17.   
18.         // Normalise accelerometer measurement  
19.         recipNorm = invSqrt(ax * ax + ay * ay + az * az);  
20.         ax *= recipNorm;  
21.         ay *= recipNorm;  
22.         az *= recipNorm;       
23.   
24.         // Normalise magnetometer measurement  
25.         recipNorm = invSqrt(mx * mx + my * my + mz * mz);  
26.         mx *= recipNorm;  
27.         my *= recipNorm;  
28.         mz *= recipNorm;     
29.   
30.         // Auxiliary variables to avoid repeated arithmetic  
31.         q0q0 = q0 * q0;  
32.         q0q1 = q0 * q1;  
33.         q0q2 = q0 * q2;  
34.         q0q3 = q0 * q3;  
35.         q1q1 = q1 * q1;  
36.         q1q2 = q1 * q2;  
37.         q1q3 = q1 * q3;  
38.         q2q2 = q2 * q2;  
39.         q2q3 = q2 * q3;  
40.         q3q3 = q3 * q3;     
41.   
42.         // Reference direction of Earth's magnetic field  
43.         hx = 2.0f * (mx * (0.5f - q2q2 - q3q3) + my * (q1q2 - q0q3) + mz * (q1q3 + q0q2));  
44.         hy = 2.0f * (mx * (q1q2 + q0q3) + my * (0.5f - q1q1 - q3q3) + mz * (q2q3 - q0q1));  
45.         bx = sqrt(hx * hx + hy * hy);  
46.         bz = 2.0f * (mx * (q1q3 - q0q2) + my * (q2q3 + q0q1) + mz * (0.5f - q1q1 - q2q2));  
47.   
48.         // Estimated direction of gravity and magnetic field  
49.         halfvx = q1q3 - q0q2;  
50.         halfvy = q0q1 + q2q3;  
51.         halfvz = q0q0 - 0.5f + q3q3;  
52.         halfwx = bx * (0.5f - q2q2 - q3q3) + bz * (q1q3 - q0q2);  
53.         halfwy = bx * (q1q2 - q0q3) + bz * (q0q1 + q2q3);  
54.         halfwz = bx * (q0q2 + q1q3) + bz * (0.5f - q1q1 - q2q2);    
55.       
56.         // Error is sum of cross product between estimated direction and measured direction of field vectors  
57.         halfex = (ay * halfvz - az * halfvy) + (my * halfwz - mz * halfwy);  
58.         halfey = (az * halfvx - ax * halfvz) + (mz * halfwx - mx * halfwz);  
59.         halfez = (ax * halfvy - ay * halfvx) + (mx * halfwy - my * halfwx);  
60.   
61.         // Compute and apply integral feedback if enabled  
62.         if(twoKi > 0.0f) {  
63.             integralFBx += twoKi * halfex * (1.0f / sampleFreq);    // integral error scaled by Ki  
64.             integralFBy += twoKi * halfey * (1.0f / sampleFreq);  
65.             integralFBz += twoKi * halfez * (1.0f / sampleFreq);  
66.             gx += integralFBx;  // apply integral feedback  
67.             gy += integralFBy;  
68.             gz += integralFBz;  
69.         }  
70.         else {  
71.             integralFBx = 0.0f; // prevent integral windup  
72.             integralFBy = 0.0f;  
73.             integralFBz = 0.0f;  
74.         }  
75.   
76.         // Apply proportional feedback  
77.         gx += twoKp * halfex;  
78.         gy += twoKp * halfey;  
79.         gz += twoKp * halfez;  
80.     }  
81.       
82.     // Integrate rate of change of quaternion  
83.     gx *= (0.5f * (1.0f / sampleFreq));     // pre-multiply common factors  
84.     gy *= (0.5f * (1.0f / sampleFreq));  
85.     gz *= (0.5f * (1.0f / sampleFreq));  
86.     qa = q0;  
87.     qb = q1;  
88.     qc = q2;  
89.     q0 += (-qb * gx - qc * gy - q3 * gz);  
90.     q1 += (qa * gx + qc * gz - q3 * gy);  
91.     q2 += (qa * gy - qb * gz + q3 * gx);  
92.     q3 += (qa * gz + qb * gy - qc * gx);   
93.       
94.     // Normalise quaternion  
95.     recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);  
96.     q0 *= recipNorm;  
97.     q1 *= recipNorm;  
98.     q2 *= recipNorm;  
99.     q3 *= recipNorm;  
100. }  

    相信有很多人已经理解了加速度计补偿陀螺仪漂移的原理，这部分代码在x-IMU官网上已经给出，大家可以自行下载(http://www.x-io.co.uk/open-source-imu-and-ahrs-algorithms/)，有能力的可以自行查看Sebastian O.H. Madgwick在2010年4月发表的一篇论文（An efficient orientation filter for inertial and inertial/magneticsensor arrays），可以发现x-IMU官网上的融合代码就是基于此篇论文。

    花了一天时间研究地磁融合代码，总算弄明白了其地磁融合的原理。为了让大家理解Madgwick对地磁量的处理方式，我先从加速度计补偿开始说起。

    首先，东北天坐标系我们称之为n系（地理坐标系，参考坐标系），载体坐标系我们称之为b系，就是我们飞行器的坐标系。对于四元数法的姿态解算，我们求的就是四元数的值；方向余弦矩阵（用于表示n系和b系的相对关系）中的元素本来应该是三角函数，这里由于我们四元数法，所以矩阵中的元素就成了四元数。所以我们的任务就是求解由四元数构成的方向余弦矩阵nCb（nCb表示从b系到n的转换矩阵，同理，bCn表示从n系到b的转换矩阵，他们的关系是转置）。

    显然，上述矩阵是有误差存在的。对于一个确定的向量n，用不同的坐标系表示时，他们所表示的大小和方向一定是相同的。但是由于这两个坐标系的转换矩阵存在误差，那么当一个向量经过这么一个有误差存在的旋转矩阵变换后，在另一个坐标系中肯定和理论值是有偏差的，我们通过这个偏差来修正这个旋转矩阵。我们刚才说了，这个旋转矩阵的元素是四元数，这就是说我们修正的就是四元数，于是乎我们的姿态就这样被修正了，这才是姿态解算的原理。

    我这里再重复一遍，因为这是原理部分。我们的姿态解算求的是四元数，我们是通过修正旋转矩阵中的四元数来达到姿态解算的目的，而不要以为通过加速度计和地磁计来修正姿态，加速度计和地磁计只是测量工具和载体，通过这两个器件表征旋转矩阵的误差存在，然后通过算法修正误差，修正四元数，修正姿态。

    在n系中，加速度计输出为，经过bCn转换之后到b中的值为；在b系中，加速度计的测量值为，现在和均表示在b系中的竖直向下的向量，由此，我们来做向量积，得到误差，利用这个误差来修正bCn矩阵，于是乎，我们的四元数就在这样一个过程中被修正了。（实际上这种修正方法只把b系和n系的XOY平面重合起来，对于z轴旋转的偏航，加速度计无可奈何，稍后给详细讲解）但是，由于加速度计无法感知z轴上的旋转运动，所以还需要用地磁计来进一步补偿。

    我们知道加速度计在静止时测量的是重力加速度，是有大小和方向的；同理，地磁计同样测量的是地球磁场的大小和方向，只不过这个方向不再是竖直向下，而是与x轴（或者y轴）呈一个角度，与z轴呈一个角度。记作，这里我们让x轴对准北边，所以by=0，即。倘若我们知道bx和bz的精确值，那么我们就可以采用和加速度计一样的修正方法来修正。只不过在加速度计中，我们在n系中的参考向量是，变成了地磁计的。如果我们知道bx和bz的精确值，那么我们就可以摆脱掉加速度计的补偿，直接用地磁计和陀螺仪进行姿态解算，但是你看过谁只有陀螺仪和地磁计进行姿态解算吗？没有，因为没人会去测量当地的地磁场相对于东北天坐标的夹角，也就是bx和bz。那么现在怎么办？

-----

    前面已经讲了，我们的姿态解算就是求解旋转矩阵，这个矩阵的作用就是将b系和n正确的转化直到重合。

    现在我们假设nCb*旋转矩阵是经过加速度计校正后的矩阵，当某个确定的向量（b系中）经过这个矩阵旋转之后（到n系），这两个坐标系在XOY平面上重合，只是在z轴旋转上会存在一个偏航角的误差。下图表示的是经过nCb*旋转之后的b系和n系的相对关系。可以明显发现加速度计可以把b系通过四元数法从任意角度拉到与n系水平的位置上，这时，只剩下一个偏航角误差。这也是为什么加速度计误差修正偏航的原因。

    到这里，就好说了。现在我们反过来从b系推往n系：设地磁计在b系中的输出为，经过nCb*旋转之后得到（n系）。在这个XOY平面上（n系），的投影为bx2,的投影为hx2+hy2。显然，地磁计在XOY平面上（n系）的向量的大小必定相同，所以有bx2= hx2+hy2。而对于bz的处理，我们不做变动，令bz=hz即可。经过这样处理之后的，经过bCn*旋转回转到b系中，得到，这个值再和b系中的地磁计输出做向量积求误差，再次修正bCn*（或者nCb*），得到bCn**（或者nCb**）。这样就完成了一次地磁计的补偿。

    将加速度计没能做到的z轴上的旋转修正，通过地磁计在XOY平面上的地磁力相同原理，得到了修正。于是乎，pitch和roll通过加速度计修正，然后在这个基础之上（该地磁计补偿方法必须依靠加速度计修正提供一致的XOY平面，才会有bx2= hx2+hy2等式成立），yaw通过地磁计来补偿，最终得到了没有偏差的实时姿态（也就是由四元数组成的旋转矩阵）。