网络模型 - 随机网络，无标度网络，分层网络

来源：互联网发布：it程杰编辑：程序博客网时间：2024/05/16 04:38

转自： http://www.flickr.com/photos/caseorganic/4510691991/in/set-72157624621620243

小图

大图

Network Models - Random network, Scale-free network, Hierarchical network

随机网络

The Erdös–Rényi (ER) model of a random network14 (see figure, part A) starts with N nodes and connects each pair of nodes with probability p,
which creates a graph with approximately pN(N–1)/2 randomly placed links (see figure, part Aa). The node degrees follow a Poisson distribution
(see figure, part Ab), which indicates that most nodes have approximately the same number of links (close to the average degree ). The tail
(high k region) of the degree distribution P(k) decreases exponentially, which indicates that nodes that significantly deviate from the average are
extremely rare. The clustering coefficient is independent of a node’s degree, so C(k) appears as a horizontal line if plotted as a function of k (see
figure, part Ac). The mean path length is proportional to the logarithm of the network size, l ~ log N, which indicates that it is characterized by the
small-world property.

无标度网络

Scale-free networks (see figure, part B) are characterized by a power-law degree distribution; the probability that a node has k links follows
P(k) ~ k –γ, where γ is the degree exponent. The probability that a node is highly connected is statistically more significant than in a random graph,
the network’s properties often being determined by a relatively small number of highly connected nodes that are known as hubs (see figure, part
Ba; blue nodes). In the Barabási–Albert model of a scale-free network15, at each time point a node with M links is added to the network, which
connects to an already existing node I with probability ΠI = kI/ΣJkJ, where kI is the degree of node I (FIG. 3) and J is the index denoting the sum over
network nodes. The network that is generated by this growth process has a power-law degree distribution that is characterized by the degree
exponent γ = 3. Such distributions are seen as a straight line on a log–log plot (see figure, part Bb). The network that is created by the
Barabási–Albert model does not have an inherent modularity, so C(k) is independent of k (see figure, part Bc). Scale-free networks with degree
exponents 2<γ<3, a range that is observed in most biological and non-biological networks, are ultra-small34,35, with the average path length
following ~ log log N, which is significantly shorter than log N that characterizes random small-world networks.

分层网络

To account for the coexistence of modularity, local clustering and scale-free topology in many real systems it has to be assumed that clusters
combine in an iterative manner, generating a hierarchical network47,53 (see figure, part C). The starting point of this construction is a small cluster
of four densely linked nodes (see the four central nodes in figure, part Ca).Next, three replicas of this module are generated and the three external
nodes of the replicated clusters
connected to the central node of
the old cluster, which produces a
large 16-node module. Three
replicas of this 16-node module
are then generated and the 16
peripheral nodes connected to
the central node of the old
module, which produces a new
module of 64 nodes. The
hierarchical network model
seamlessly integrates a scale-free
topology with an inherent
modular structure by generating
a network that has a power-law
degree distribution with degree
exponent γ = 1 + n4/n3 = 2.26
(see figure, part Cb) and a large,
system-size independent average
clustering coefficient ~ 0.6.
The most important signature of
hierarchical modularity is the
scaling of the clustering
coefficient, which follows
C(k) ~ k –1 a straight line of slope
–1 on a log–log plot (see figure,
part Cc). A hierarchical
architecture implies that sparsely
connected nodes are part of
highly clustered areas, with
communication between the
different highly clustered
neighbourhoods being
maintained by a few hubs
(see figure, part Ca).

From Network Biology - Understanding the Cell's Functional Organization. Albert Laszlo Barabasi, Zoltan Oltvai 2004.

About the Authors
Albert-László Barabási is the Emil T. Hofman Professor of physics
at the University of Notre Dame, USA. His research group introduced
the concept of scale-free networks and studied their relevance
to biological and communication systems. He obtained his
M.Sc. degree in physics in 1991 from Eötvös Loránd University,
Budapest, Hungary, and his Ph.D. in 1994 from Boston University,
USA. After a year as a postdoctoral fellow at IBM Thomas J.
Watson Research Center, USA, he joined the University of Notre
Dame in 1995. He is a fellow of the American Physical Society, and
the author of the general audience book Linked: The New Science of
Networks.
Zoltán Nagy Oltvai is an assistant professor of pathology at
Northwestern University’s Feinberg School of Medicine, USA. His
clinical interest is molecular pathology and he is the director of
diagnostic molecular pathology at the medical school and
Northwestern Memorial Hospital. His research group’s interest is
the theoretical and experimental study of intracellular molecular
interaction networks. He received his M.D. degree from
Semmelweiss Medical University, Budapest, Hungary, and did his
clinical pathology/molecular biology research residency at
Washington University/Barnes Hospital in St. Louis, USA.

看不懂英文的看中文的，写的还可以

参考：http://www.cnblogs.com/peon/archive/2009/08/23/1552472.html

[笔记+整理]随机网络和无标度网络

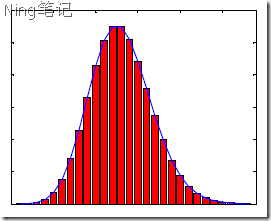
传统的随机网络（如ER模型），尽管连接是随机设置的，但大部分节点的连接数目会大致相同，即节点的分布方式遵循钟形的泊松分布，有一个特征性的“平均数”。连接数目比平均数高许多或低许多的节点都极少，随着连接数的增大，其概率呈指数式迅速递减。故随机网络亦称指数网络。

节点连接数的泊松分布：

一个随机网络：

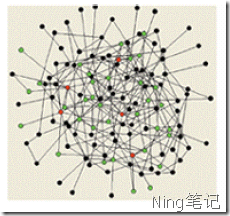
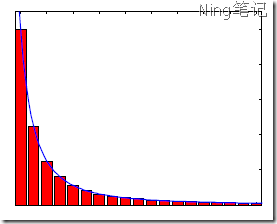
现实世界的网络大部分都不是随机网络，少数的节点往往拥有大量的连接，而大部分节点却很少，一般而言他们符合zipf定律，(也就是80/20马太定律)。人们给具有这种性质的网络起了一个特别的名字——无标度网络。这里的无标度是指网络缺乏一个特征度值（或平均度值），即节点度值的波动范围相当大。

节点连接数的zipf分布：

符合zipf分布的无标度网络：

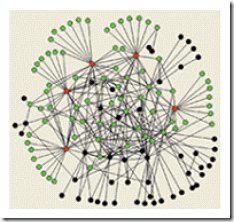
现实中的交通网，电话网和Internet都是无标度网络，在这种网络中，存在拥有大量连接的集散节点，比如交通枢纽就是这样的节点。下面是Internet的连接模型：

分布满足幂律的无标度网络还有一个奇特的性质——“小世界”特性[49]，虽然WWW中的页面数已超过80亿，但平均来说，在WWW上只需点击19次超链接，就可从一个网页到达任一其它页面。“小世界”现象在社会学上也称为“六度分离”。

Barabási与Albert针对复杂网络中普遍存在的幂律分布现象，提出了网络动态演化的BA模型[42, 59]，他们解释，成长性和优先连接性是无标度网络度分布呈现幂律的两个最根本的原因。所谓成长性是指网络节点数的增加，像Internet中自治系统或路由器的添加，以及WWW中网站或网页的增加等，优先连接性是指新加入的节点总是优先选择与度值较高的节点相连，比如，新网站总是优先选择人们经常访问的网站作为超链接。随着时间的演进，网络会逐渐呈现出一种“富者愈富，贫者愈贫”的现象。社会学家所说的“马太效应”[72]，《新约》圣经所说的“凡有的，还要加给他，叫他有余”，同优先连接也有某种相通之处。

引用：

幂律分布研究简史

无标度网络及其系统科学意义

下面是我的其他博客：
博客园，写一些工作和学习的笔记： http://www.cnblogs.com/peon/
博客堂，开发方面的一些文章：http://blog.joycode.com/peon/
流媒体博客，流媒体方面的一些文章：http://blog.lmtw.com/b/peon/

0 0