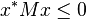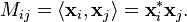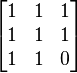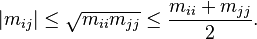正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
来源:互联网 发布:数据挖掘的案例分析 编辑:程序博客网 时间:2024/05/01 08:10
正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
载▼
1.正定矩阵
2.负定矩阵
 是负定矩阵当且仅当对所有不为零的
是负定矩阵当且仅当对所有不为零的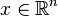 (或
(或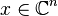 ),都有:
),都有:

3.半正定矩阵
 是半正定矩阵当且仅当对所有不为零的
是半正定矩阵当且仅当对所有不为零的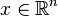 (或
(或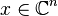 ),都有:
),都有:
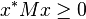
4.半负定矩阵
 是半负定矩阵当且仅当对所有不为零的
是半负定矩阵当且仅当对所有不为零的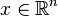 (或
(或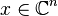 ),都有:
),都有:
正定阵的判别[编辑]
对n×n的埃尔米特矩阵M,下列性质与“M为正定矩阵”等价:
1.矩阵 的所有的特征值
的所有的特征值 都是正的。根据谱定理,M必然与一个实对角矩阵D相似(也就是说
都是正的。根据谱定理,M必然与一个实对角矩阵D相似(也就是说 ,其中P是幺正矩阵,或者说M在某
,其中P是幺正矩阵,或者说M在某个正交基可以表示为一个实对角矩阵)。因此,M是正定阵当且仅当相应的D的对角线上元素都是正的。2.半双线性形式
定义了一个Cn上的内积。实际上,所有Cn上的内积都可看做由某个正定阵通过此种方式得到。
3.M是n个线性无关的k维向量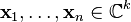 的Gram矩阵,其中的k为某个正整数。更精确地说,M定义为:
的Gram矩阵,其中的k为某个正整数。更精确地说,M定义为:换句话说,M具有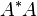 的形式,其中A不一定是方阵,但需要是单射的。
的形式,其中A不一定是方阵,但需要是单射的。
 左上角1×1的矩阵
左上角1×1的矩阵 左上角2×2矩阵
左上角2×2矩阵- ...
 自身。
自身。
对于半正定矩阵来说,相应的条件应改为所有的主子式非负。顺序主子式非负并不能推出矩阵是半正定的。比如以下例子:
 ,其主对角线上的元素全是正的,使得:
,其主对角线上的元素全是正的,使得: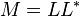 .
.
其中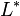 是
是 的共轭转置。 T这一分解被称为Cholesky分解。
的共轭转置。 T这一分解被称为Cholesky分解。
对于实对称矩阵,只需将上述性质中的 改为
改为 ,将“共轭转置”改为“转置”就可以了。
,将“共轭转置”改为“转置”就可以了。
相关性质[编辑]
若 为半正定阵,可以写作
为半正定阵,可以写作 。如果
。如果 是正定阵,可以写作
是正定阵,可以写作 。这个记法来自泛函分析,其中的正定阵定义了正算子。
。这个记法来自泛函分析,其中的正定阵定义了正算子。
对于一般的埃尔米特矩阵, 、
、 ,
,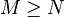 当且仅当
当且仅当 。这样可以定义一个在埃尔米特矩阵集合上的偏序关系。类似地,可以定义
。这样可以定义一个在埃尔米特矩阵集合上的偏序关系。类似地,可以定义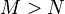 。
。
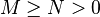 那么
那么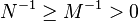 。2.如果
。2.如果 是正定阵,
是正定阵,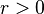 为正实数,那么
为正实数,那么 也是正定阵。
也是正定阵。如果 、
、 是正定阵,那么和
是正定阵,那么和 、乘积
、乘积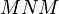 与
与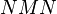 都是正定的。如果
都是正定的。如果 ,那么
,那么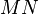 仍是正定阵。
仍是正定阵。
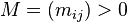 那么主对角线上的系数
那么主对角线上的系数 为正实数。于是有
为正实数。于是有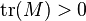 。此外还有
。此外还有 是正定阵当且仅当存在唯一的正定阵
是正定阵当且仅当存在唯一的正定阵 使得
使得 。根据其唯一性可以记作
。根据其唯一性可以记作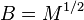 ,称
,称 为
为 的平方根。对半正定阵也有类似结论。同时,如果
的平方根。对半正定阵也有类似结论。同时,如果 那么
那么 .5.如果
.5.如果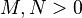 那么
那么 ,其中
,其中 表示克罗内克乘积。6.对矩阵
表示克罗内克乘积。6.对矩阵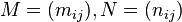 ,将两者同一位置上的系数相乘所得的矩阵记为
,将两者同一位置上的系数相乘所得的矩阵记为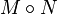 ,即
,即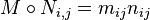 ,称为
,称为 与
与 的阿达马乘积。如果
的阿达马乘积。如果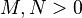 ,那么
,那么 。如果
。如果 为实系数矩阵,则有如下不等式成立:
为实系数矩阵,则有如下不等式成立:
 ,
, 为埃尔米特矩阵。如果
为埃尔米特矩阵。如果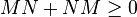 (
( ),那么
),那么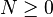 (
(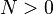 )。8.如果
)。8.如果 为实系数矩阵,则
为实系数矩阵,则 。9.如果
。9.如果 为实系数矩阵,那么存在
为实系数矩阵,那么存在 使得
使得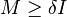 ,其中
,其中 为单位矩阵。
为单位矩阵。from:
http://zh.wikipedia.org/wiki/正定矩阵
阅读全文
0 0
- 正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
- 正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
- 正定矩阵
- 正定矩阵
- 正定矩阵
- 半正定矩阵
- 半正定矩阵理解
- 半正定矩阵是闭凸锥
- 矩阵的正定与半正定
- 正定、超定、欠定矩阵
- 证明:协方差矩阵是半正定矩阵
- 如何判定正定矩阵
- 正定矩阵的意义
- soledede--正定Hessian矩阵
- matlab产生正定矩阵
- MIMO中矩阵的小笔记(正定,半正定)
- 正定、负定矩阵的猜想——logm and expm
- 正定对称矩阵快速求解
- Socket编程(网络协议一)
- Linphone-android 登录过程增加自定义消息头流程分析
- 各种排序算法总结
- java html转pdf 中文乱码
- Markdown
- 正定矩阵、负定矩阵、半正定矩阵、半负定矩阵
- deformable convolutional networks
- Redis集群
- python自学2
- 整合spring session 用redis 做缓存
- ④NuPlayer播放框架之Renderer源码分析
- 分享Kali Linux 2017年第24周镜像文件
- 从零开始使用Eclipse搭建NDK项目
- 17 《一条改变世界的鱼:鳕鱼往事》 -豆瓣评分8.9