树状数组

转载两篇好文章收藏

在topcoder的网站上了解到树状数组这个结构是在设计压缩算法时被发现的。这个数据结构真是天才的构想，膜拜！

树状数组的基础是一个被构造出来的式子:C[i]=A[i]+A[i-1]+....+A[i-2^k+1];k代表i的二进制的最后连续0的个数 比如 对于1000和101000，k=3。至于这个式子是怎么被构造出来的，k为什么要代表这个。因为二进制的思想。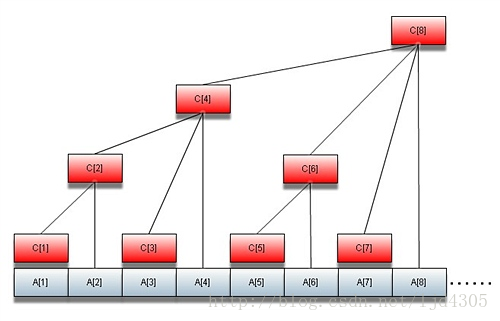

根据这个图来看节点与其子树的关系

接下来则很容易发现 节点和子节点的是有关系的，这种关系就是 i=j+lowbit(j); lowbit是j的最低位1所代表的数字 比如对于 1000(8的二进制) 1000=100+lowbit(100)=110+lowbit(110)=111+lowbit(111);

这个关系是树状数组的核心，有了这个关系，我们可以把子区间的变化以log2n的次数传递上去

那我们也知道了 当我们要求 1-n的和时，我们同样把n表示为2进制，我们知道 C[i]=A[i]+A[i-1]+....+A[i-2^k+1]; 所以对于i 是不是我们只要把他所有的1都用上 就可以表示1-n的和？

举个例子 求1-11000 则 Sum(11000)=C[11000]+C[10000]; 因为 根据C[i]的构造方法 C[i]是从A[i]开始的2^k个元素的和，则C[11000]求了A[11000] A[10111] A[10110] A[10101] A[10100] A[10010] A[10001] 这2^k个数 然后接着C[10000]求出了剩下 10000个元素的和 到了这我们就大概了解了树状数组的发明者的天才的构造是从何而来的了 普通的求1-n的和储存的数据太多，而这位天才则想，我们能不能根据二进制的思想来储存这些值呢？任何一个数，都可以由若干个二进制数相加而成，如果我们在求Sum(n)之前就知道了 n对应的二进制数从最低位开始，每个1所代表的数字的前2^i个数的和，我们不就能在时间复杂度log2(n)内求出所有的值 比如 101110 我们如果知道 101110->101101 101100->101001 101000->100001 100000->1各自的和，就可以在空间复杂度和时间复杂度很小的情况下求出1-101110了

然后对于区间和的修改 又利用每个小区间向上转移 修改了大区间的和

总的来说 树状数组就是利用了二进制的思想求和 写的有点乱 但只要你看懂了 二进制思想的那部分 相信看懂和实现树状数组并不难

一、树状数组是干什么的？

       平常我们会遇到一些对数组进行维护查询的操作，比较常见的如，修改某点的值、求某个区间的和，而这两种恰恰是树状数组的强项！当然，数据规模不大的时候，对于修改某点的值是非常容易的，复杂度是O(1)，但是对于求一个区间的和就要扫一遍了，复杂度是O(N)，如果实时的对数组进行M次修改或求和，最坏的情况下复杂度是O(M*N)，当规模增大后这是划不来的！而树状数组干同样的事复杂度却是O(M*lgN)，别小看这个lg，很大的数一lg就很小了，这个学过数学的都知道吧，不需要我说了。申明一下，看下面的文章一定不要急，只需要看懂每一步最后自然就懂了。

二、树状数组怎么干的？

        先看两幅图（网上找的，如果雷同，不要大惊小怪～），下面的说明都是基于这两幅图的，左边的叫A图吧，右边的叫B图：

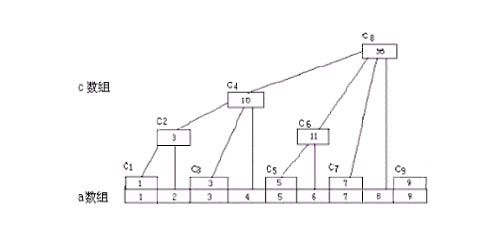
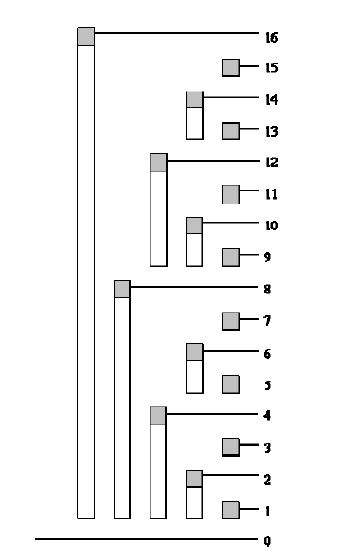
      是不是很像一颗树？对，这就是为什么叫树状数组了～先看A图，a数组就是我们要维护和查询的数组，但是其实我们整个过程中根本用不到a数组，你可以把它当作一个摆设！c数组才是我们全程关心和操纵的重心。先由图来看看c数组的规则，其中c8 = c4+c6+c7+a8，c6 = c5+a6……先不必纠结怎么做到的，我们只要知道c数组的大致规则即可，很容易知道c8表示a1～a8的和，但是c6却是表示a5～a6的和，为什么会产生这样的区别的呢？或者说发明她的人为什么这样区别对待呢？答案是，这样会使操作更简单！看到这相信有些人就有些感觉了，为什么复杂度被lg了呢？可以看到，c8可以看作a1～a8的左半边和+右半边和，而其中左半边和是确定的c4，右半边其实也是同样的规则把a5～a8一分为二……继续下去都是一分为二直到不能分，可以看看B图。怎么样？是不是有点二分的味道了？对，说白了树状数组就是巧妙的利用了二分，她并不神秘，关键是她的巧妙！

       她又是怎样做到不断的一分为二呢？说这个之前我先说个叫lowbit的东西，lowbit(k)就是把k的二进制的高位1全部清空，只留下最低位的1,比如10的二进制是1010,则lowbit(k)=lowbit(1010)=0010(2进制)，介于这个lowbit在下面会经常用到，这里给一个非常方便的实现方式，比较普遍的方法lowbit(k)=k&-k，这是位运算，我们知道一个数加一个负号是把这个数的二进制取反+1，如-10的二进制就是-1010=0101+1=0110，然后用1010&0110，答案就是0010了！明白了求解lowbit的方法就可以了，继续下面。介于下面讨论十进制已经没有意义（这个世界本来就是二进制的，人非要主观的构建一个十进制），下面所有的数没有特别说明都当作二进制。

       上面那么多文字说lowbit，还没说它的用处呢，它就是为了联系a数组和c数组的！ck表示从ak开始往左连续求lowbit(k)个数的和，比如c[0110]=a[0110]+a[0101]，就是从110开始计算了0010个数的和，因为lowbit(0110)=0010，可以看到其实只有低位的1起作用，因为很显然可以写出c[0010]=a[0010]+a[0001]，这就为什么我们任何数都只关心它的lowbit，因为高位不起作用（基于我们的二分规则它必须如此！），除非除了高位其余位都是0，这时本身就是lowbit。

既然关系建立好了，看看如何实现a某一个位置数据跟改的，她不会直接改的（开始就说了，a根本不存在），她每次改其实都要维护c数组应有的性质，因为后面求和要用到。而维护也很简单，比如更改了a[0011]，我们接着要修改c[0011],c[0100],c[1000]，这是很容易从图上看出来的，但是你可能会问，他们之间有申明必然联系吗？每次求解总不能总要拿图来看吧？其实从0011——>0100——>1000的变化都是进行“去尾”操作，又是自己造的词--''，我来解释下，就是把尾部应该去掉的1都去掉转而换到更高位的1,记住每次变换都要有一个高位的1产生，所以0100是不能变换到0101的，因为没有新的高位1产生，这个变换过程恰好是可以借助我们的lowbit进行的，k +=lowbit(k)。

       好吧，现在更新的次序都有了，可能又会产生新的疑问了：为什么它非要是这种关系啊？这就要追究到之前我们说c8可以看作a1～a8的左半边和+右半边和……的内容了，为什么c[0011]会影响到c[0100]而不会影响到c[0101]，这就是之前说的c[0100]的求解实际上是这样分段的区间 c[0001]~c[0001] 和区间c[0011]~c[0011]的和，数字太小，可能这样不太理解，在比如c[0100]会影响c[1000]，为什么呢？因为c[1000]可以看作0001～0100的和加上0101~1000的和，但是0101位置的数变化并会直接作用于c[1000]，因为它的尾部1不能一下在跳两级在产生两次高位1,是通过c[0110]间接影响的，但是，c[0100]却可以跳一级产生一次高位1。

         可能上面说的你比较绕了，那么此时你只需注意：c的构成性质（其实是分组性质）决定了c[0011]只会直接影响c[0100]，而c[0100]只会直接影响[1000]，而下表之间的关系恰好是也必须是k +=lowbit(k)。此时我们就是写出跟新维护树的代码：

[cpp] view plain copy

 print?

1. void add(int k,int num)  
2. {  
3.     while(k<=n)  
4.     {  
5.         tree[k]+=num;  
6.         k+=k&-k;  
7.     }  
8. }  

       有了上面的基础，说求和就比较简单了。比如求0001～0110的和就直接c[0100]+c[0110]，分析方法与上面的恰好逆过来，而且写法也是逆过来的，具体就不累述了：

[cpp] view plain copy

 print?

1. int read(int k)//1~k的区间和  
2. {  
3.     int sum=0;  
4.     while(k)  
5.     {  
6.         sum+=tree[k];  
7.         k-=k&-k;  
8.     }  
9.     return sum;  
10. }  

三、总结一下吧

          首先，明白树状数组所白了是按照二分对数组进行分组；维护和查询都是O(lgn)的复杂度，复杂度取决于最坏的情况，也是O(lgn);lowbit这里只是一个技巧，关键在于明白c数组的构成规律;分析的过程二进制一定要深入人心，当作心目中的十进制。