hihocoder 1151 : 骨牌覆盖问题·二（找规律+矩阵快速幂）

骨牌覆盖问题·二

描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：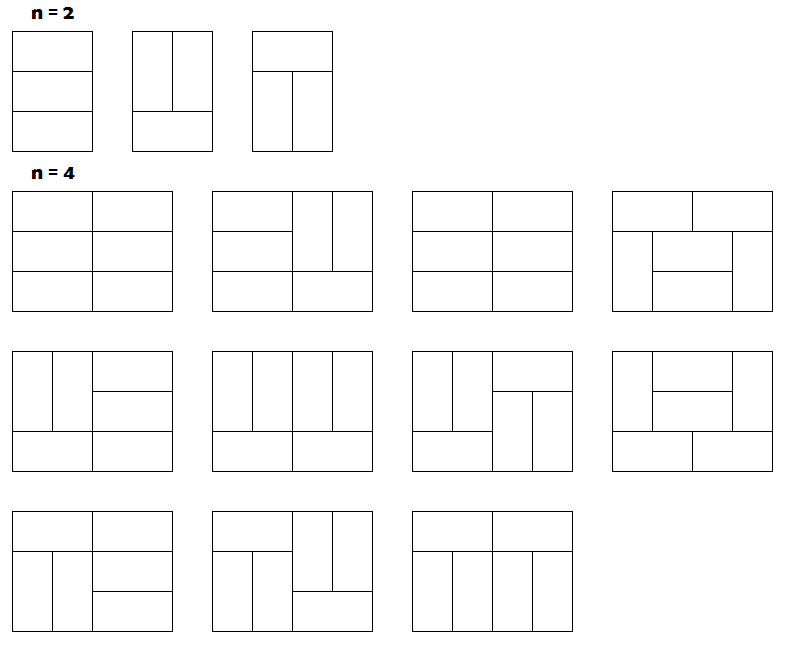

提示：3xN骨牌覆盖

输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入
62247088
样例输出
4037


提示：
在2xN的骨牌覆盖问题中，我们有递推式子 (0,1)xM^n=(f[n-1],f[n])。
我们考虑能否在3xN的情况下找到同样的式子。
但在实际的推导过程可以发现，对于3xN的覆盖，对应的f数值公式比2xN复杂太多。我们需要换个角度来思考推导公式。

在我们放置骨牌的过程中，一定是放好一行之后再放置下一行。根据摆放的方式，可能会产生很多种不同的形状，而这些形状之间是否具有某些递推关系呢？
如果他们存在一定的递推关系，则我们可以根据第i行的方案数来推导第i+1行的方案数。这样一行一行推导，直到第N行时不就得到了我们要求的方案数了么？
那么来研究一下是否存在这样的推导公式吧

假设我们已经放好了一些骨牌，对于当前最后一列(第i列)骨牌，可能有8种情况：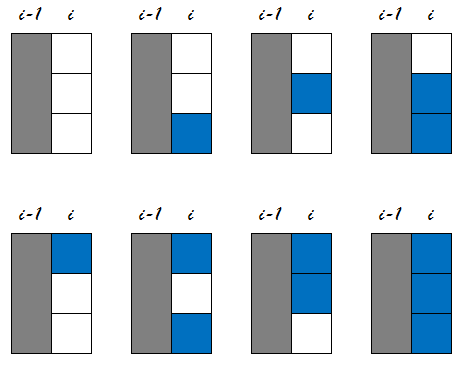

对于上面这8种状态，我们用数字来标记它们。以有放置骨牌的格子为1，未放置为0，转化为2进制数
以最下面一行作为1，则有：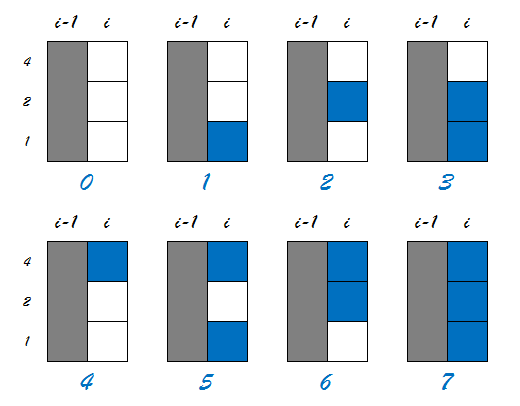

接下来考虑如何放置骨牌，我们先将棋盘旋转一下。假设我们正在放置第i行的骨牌，那么会有下面3种方式：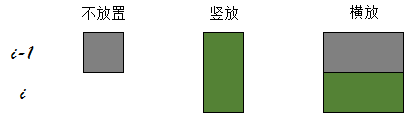

灰色表示已经有的骨牌，绿色表示新放置的骨牌。
每一种放置方法解释如下，假设当第i行的状态为x，第i-1行的状态为y：

第i行不放置，则前一行必须有放置的骨牌。x对应二进制位为0，y对应二进制位为1。
第i行竖放骨牌，则前一行必须为空。x对应二进制位为1，y对应二进制位为0。
第i行横向骨牌，则前一行必须两个位置均有骨牌，否则会产生空位。x对应二进制位为1，y对应二进制位为1。

举个例子：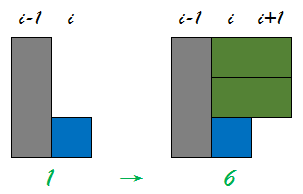

对于第i行状态1，我们在第i+1行竖放两块骨牌之后便能到达状态6。
但是在这之中需要注意会出现下面这种情况：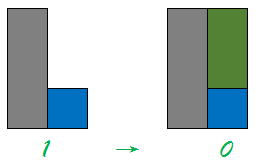

这种情况看似是从状态1变成了状态0，其实是不对的。它不满足我们约定的放置方法，本质是第i行的状态1变成了第i行的状态7，而实际上我们应该放置的是第i+1行。
所以在枚举递推关系的时候一定要注意。
通过枚举8种状态到8种状态的转移，我们可以得到一个8x8的矩阵M（空白的地方均为0）：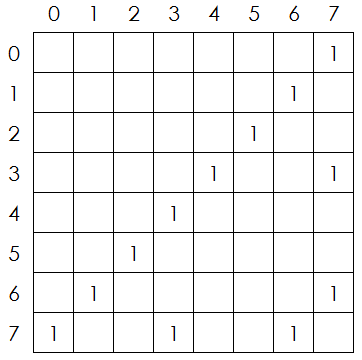

m[i][j]表示从状态i变成状态j的方案数。

现在我们有了M矩阵，接下来考虑边界情况。
在2xN的骨牌覆盖中，有(0, 1)作为初始向量A，那么在3xN中初始向量A是如何呢？
让我们先想想A向量所代表的含义。M矩阵表示状态到状态的转移，则A向量所表示的应该就是第0行各状态的方案数。
同理，对于A * M^n所求出的结果则应该表示为第n行各种状态的方案数。
那么A向量应该是多少呢？很显然，第0行在我们递推的过程中必须看作状态7才合理。故A向量表示为：
{0, 0, 0, 0, 0, 0, 0, 1}
而对于我们寻求的答案，自然也是第n行放置为状态7的方案数了。

代码：

#include<stdio.h>#include<string.h>#include<algorithm>using namespace std;#define N 8typedef long long LL;const LL mod=12357;struct Matrix{    LL mat[N][N];} tmp;Matrix M_matrix=//转置矩阵{    0,0,0,0,0,0,0,1,    0,0,0,0,0,0,1,0,    0,0,0,0,0,1,0,0,    0,0,0,0,1,0,0,1,    0,0,0,1,0,0,0,0,    0,0,1,0,0,0,0,0,    0,1,0,0,0,0,0,1,    1,0,0,1,0,0,1,0,};Matrix mul(Matrix a,Matrix b){    Matrix res;    for(LL i=0; i<N; ++i)        for(LL j=0; j<N; ++j)        {            res.mat[i][j]=0;            for(LL k=0; k<N; ++k)                res.mat[i][j]=(res.mat[i][j]+a.mat[i][k]*b.mat[k][j])%mod;        }    return res;}Matrix pow_matrix(Matrix ans,LL n){    Matrix res=M_matrix;    while(n)    {        if(n&1)            ans=mul(ans,res);        res=mul(res,res);        n>>=1;    }    return ans;}int main(){    LL n;    scanf("%d",&n);    if(n&1)        printf("0\n");    else    {        Matrix tot;        tmp.mat[0][7]=1;        tot=pow_matrix(tmp,n-1);        LL ans=0;        for(int i=0; i<N; ++i)            ans+=tot.mat[0][i];        printf("%lld\n",ans%mod);    }    return 0;}

除此之外，还有个递推公式：f[n]=3*f[n-2]+2*f[n-4]+2*f[n-6]+…….+2*f[0]；
递推证明链接：寻找&星空の孩子