Vijos[1983]NOIP2015Day2T3 运输计划 transport LCA

题目链接Vijos

题目链接UOJ

该博客在博客园的链接

【题解】--转载  NOIP2015 Day2 银牌爷题解

主要考察二分查找、树上倍增、贪心、“树上前缀和”。
题目是一颗树，要求将一条边的权值变为 $0$，使得所有运输计划的最大时间最小。
直觉告诉我们，这是一个树上倍增的题目，但是它却不像前几年的 Day2 T3 开车旅行那样纯倍增，或许更像疫情控制一些，倍增只是辅助算法，还需要配合其他算法。
由于要使所有运输计划的最大时间最小，不难想到二分答案的方法。
使 $C(t)$ 表示是否可以改造一条边，使得改造之后所有运输计划中最长的时间不大于 $t$。这是惯用伎俩，用二分的的话，我们就可以确定一个变量 $t$，正因为有了这个 $t$，我们才能有的放矢的进行贪心或是干别的。
如何判断 $C(t)$ 呢？在开始的时候用倍增预处理出所有计划的时间，如果小于等于 $t$，就可以忽略，如果大于 $t$，那么就要考虑在其路径上改造一条边。
由于所有时间大于 $t$ 的计划都要改造一条边，问题就变为了求所有时间大于 $t$ 的计划的路径交集，改造其中一条最大的边，看看去掉这条边之后，是否可以满足条件。
问题来了，如何求交集呢？
这里给出两种方法，一种是模拟求交集。一种是利用树上前缀和求交集。

方法一

对于两条路径来说，记它们的起始点分别为 $a,b,c,d$，则它们路径的交集的两个端点只有可能在六个点之间，即 $LCA(a,b),LCA(a,c),LCA(a,d),LCA(b,c),LCA(b,d),LCA(c,d)$，我们可以枚举其中两个点，看这条路径是否在都两条路径之中，而且这条路径要尽可能的长。

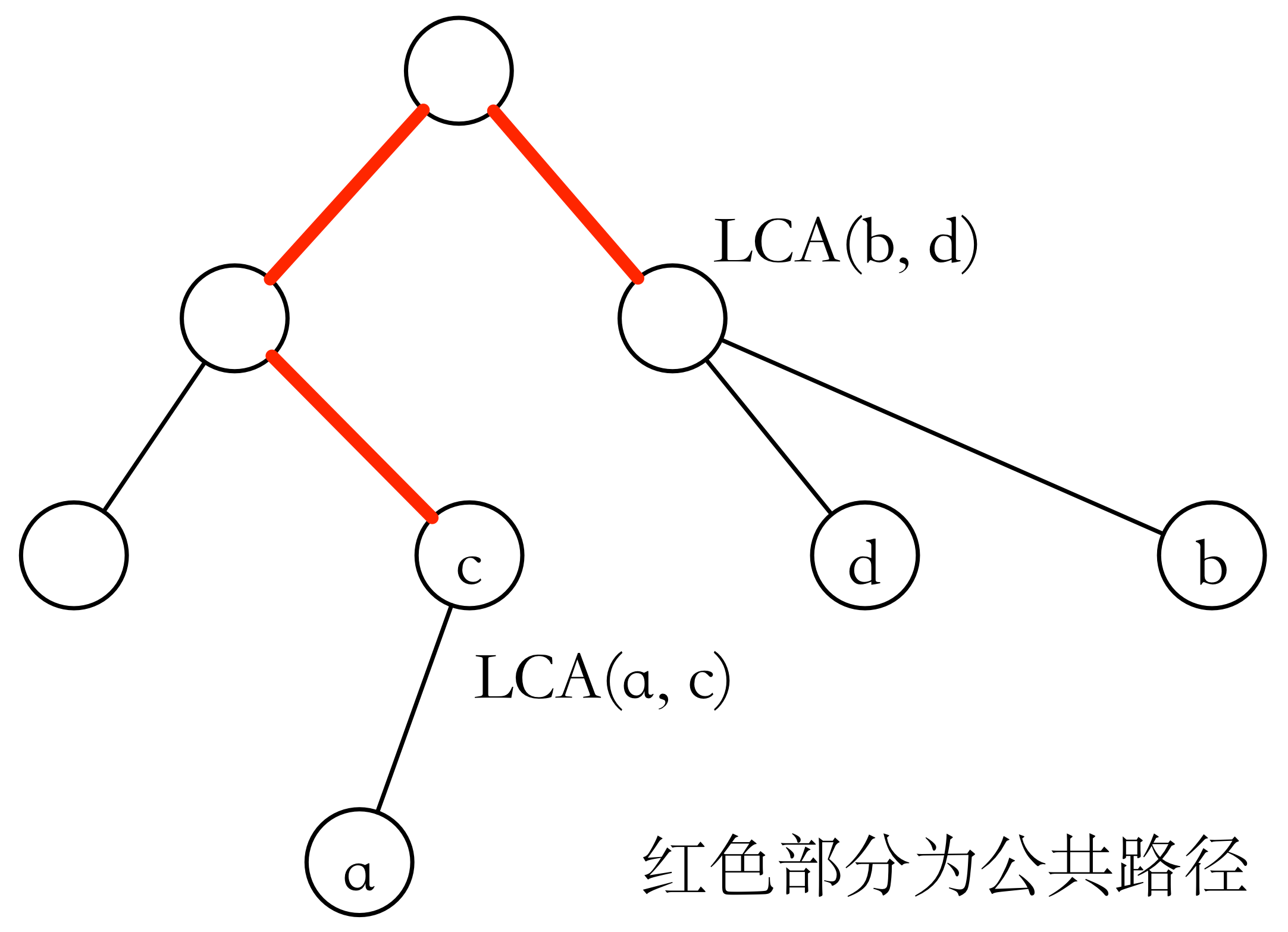
最后所有边按上面的方法顺次求交集就可以了，细节见代码一。

方法二

如果设 $total$ 为超出时间 $t$ 的方案数量，边 e_{i}e​i​​ 经过的次数 cnt_{i}cnt​i​​。对于每个超出时间 $t$ 的方案，将其路径中边的 $cnt$ 加 $1$。最后，所有 cnt_{i} = totalcnt​i​​=total 的边就是我们要求的的交集。
然而每次给每条边加一肯定是不现实的，所以我们要想出一个高效的方法，来维护边被经过的次数。
这个方法像极了2012年NOIP的 借教室 ，不过是树上的版本。我们先看看借教室的怎么处理区间加减的。
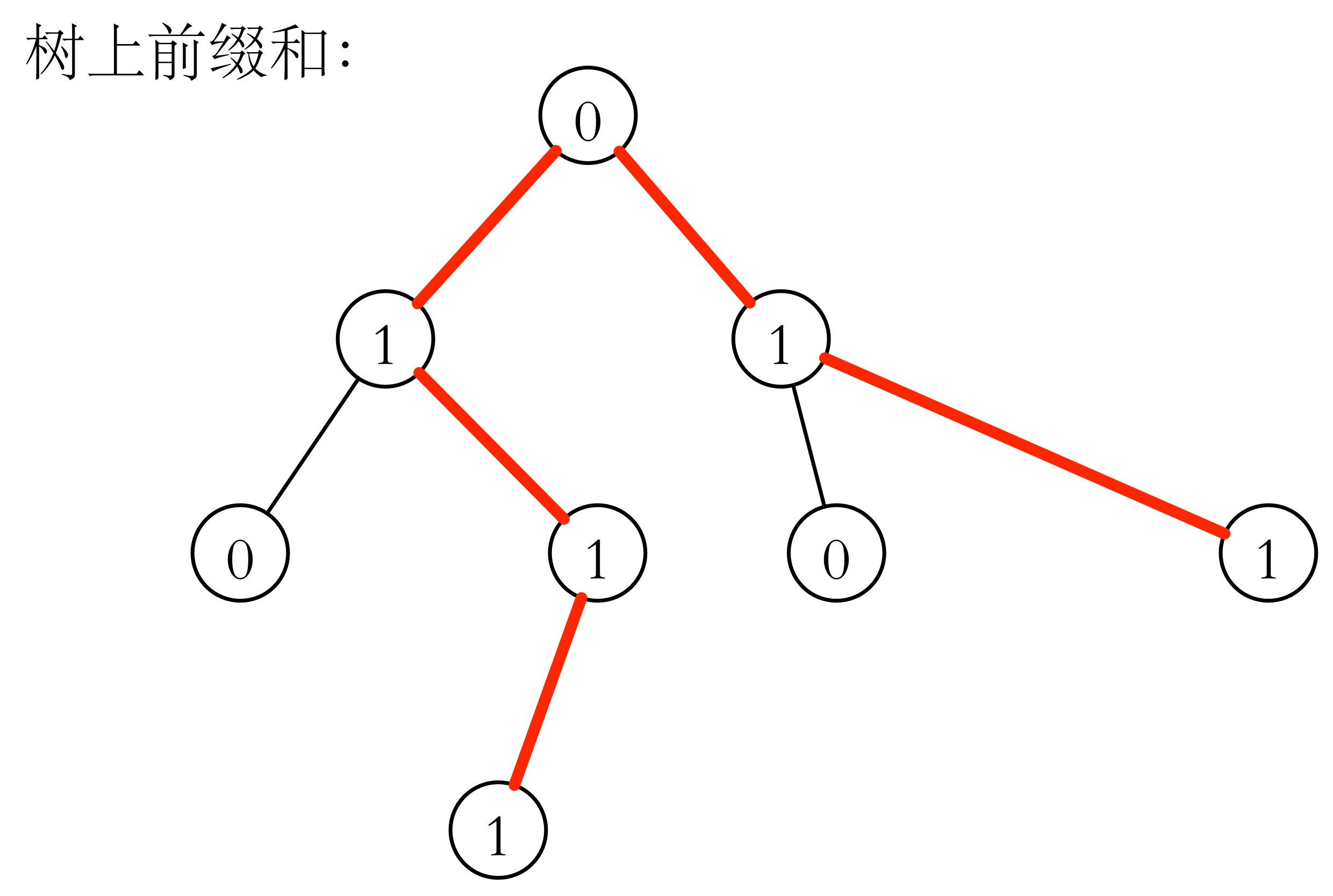
如果要对一段连续区间 $[a,b)$ 同时加上一个值，只需在开始处加上这个值，在结束后减去这个值，维护前缀和就行了。看上去应该是这样的：

若初始都是 $0$，让连续区间 $[a,b)$ 同时加上一个值 $m$ 之后，前缀和 S_{i} = \sum_0^iv_iS​i​​=∑​0​i​​v​i​​ 即为元素 $i$ 的值。下面是前缀和：

如果有多组加减，也不会冲突。
同样的，在树上，我们用 s_is​i​​ 来表示顶点 $i$ 到其父亲的这条边被经过的次数，v_iv​i​​ 用于记录顶点信息。
对于每个点对 $(a,b)$，我们将 v_a + 1, v_b + 1, v_{LCA(a, b)} - 2v​a​​+1,v​b​​+1,v​LCA(a,b)​​−2。

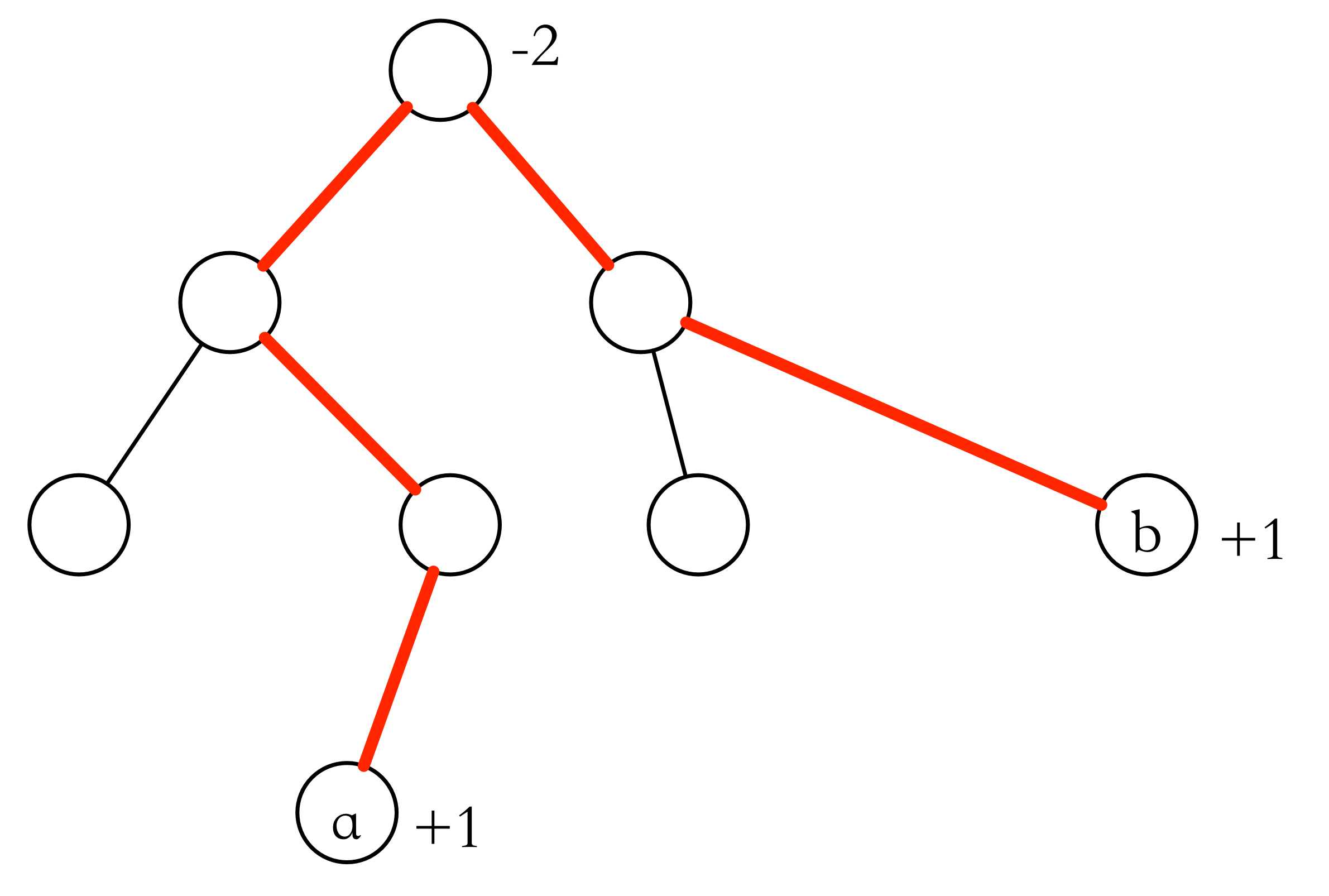
则树上前缀和 s_{i} = \sum\limits_{k \in son(i)}{v_k}s​i​​=​k∈son(i)​∑​​v​k​​。

利用 $dfs$ 序，对于每个点更新它的父亲的 $s$ 值，前缀和可以在 $O(n)$ 的时间内算出来。这样，每条边经过的次数就顺利计算出来了。
这个方法的复杂度是线性的，为 $O(m+n)$。

当然我本人写代码也是写的很艰辛：

我力劝C++的同胞们，这题卡常数，Dfs党会吃亏，比如这里这个UOJ的数据

 

我们可以使用Bfs和尽量避免写Dfs,不然会Tle的

以下代码实测极端数据约900ms，正所谓卡常数，如果把一开始的dfs改为bfs可能会更快……（博主很懒，不改了）

总结一下大佬的题解：

1. Dfs或Bfs构建树，然后记录下各种信息，现在主要是以下几点：

　　1）子节点　　　　　　son[rt]　　　　vector <int>

　　2）深度　　　　　　　deep[rt]　　　 int

　　3）到根节点的距离　　dis[rt]　　　　int

　　4）到父亲节点的距离　fadis[rt]　　　int

　　5）父亲　　　　　　　father[rt]　　　int

2. LCA的预处理，处理出F[rt][i],表示节点rt的第2ⁱ个祖先（即节点rt的祖先中与之深度相差rt的祖先）    // F[rt][i]  在代码中写成 Anst[rt][i]

     转移表达式为：F[rt][i]=F[F[rt][i-1]][i-1] 应该都能够理解

3. 求取LCA: 这里用的倍增的方法，虽然比离线算法LCA_Tarjan慢一个log，但是倍增是一个好东西，不妨去练练。这样思考：对于两个深度为d的节点a和b，使得int i=log2(d),那么就可以倍增：对于节点a和b，如果他们的第2ⁱ个祖先是相同的，那么他们在网上的祖先也一定是相同的 ，那么我们就对于不改变a和b的值，而使i=i-1；如果他们的第2ⁱ个祖先不同，那么他们往下走的祖先也是不同的，于是就可以确定他们的最近公共祖先一定是在第2ⁱ个祖先上面的，那么我们就可以安心的把a和b的值更新乘F[a][i]和F[b][i](a=F[a][i],b=F[b][i])。直到i为0位置，无法再做了。于是，a和b的最近公共祖先就是a和b的父亲，即F[a][0]或F[b][0](相等的)。于是剩下的只是把a和b调到同一深度这点事情了。设b为深度更大的那个，设deep[x]为x的深度，那么把b移上去，就是求b个第(deep[b]-deep[a])个祖先，也是倍增可以解决的。

    至于LCA_Tarjan，可以自己学啊！这里就不多说了。

3.二分答案：不用说了吧，就是一个基本的二分

4.check(答案):这个在大佬的题解里面写的比较详细，可以看他的~

【代码】

#pragma comment(linker, "/STACK:10240000,10240000")#include <cstring>#include <algorithm>#include <cstdio>#include <cstdlib>#include <cmath>#include <vector>using namespace std;const int N=300000+5,M=N*2,Inf=N*1000;void read(int &x){x=0;char ch=getchar();while (!('0'<=ch&&ch<='9'))ch=getchar();while ('0'<=ch&&ch<='9'){x=x*10+ch-48;ch=getchar();}}struct Edge{int cnt,y[M],z[M],nxt[M],fst[N];void set(){cnt=0;memset(y,0,sizeof y);memset(z,0,sizeof z);memset(nxt,0,sizeof nxt);memset(fst,0,sizeof fst);}void add(int a,int b,int c){cnt++;y[cnt]=b,z[cnt]=c;nxt[cnt]=fst[a],fst[a]=cnt;}}e;int n,m;vector <int> Tree[N];int father[N],son[N],deep[N],dis[N],fadis[N],bh[N],bhtot;int Anst[N][20];//Ancestorstruct Query{int x,y,LCA,cost;}q[N];int Nextsum[N];void Build_Tree(int prev,int rt){bh[++bhtot]=rt;Tree[rt].clear();deep[rt]=deep[prev]+1;son[rt]=0;father[rt]=prev;for (int i=e.fst[rt];i;i=e.nxt[i])if (e.y[i]!=prev){son[rt]++,Tree[rt].push_back(e.y[i]);fadis[e.y[i]]=e.z[i];dis[e.y[i]]=dis[rt]+e.z[i];Build_Tree(rt,e.y[i]);}}void LCA_Prepare(){memset(Anst,0,sizeof Anst);for (int i=1;i<=n;i++){int rt=bh[i];Anst[rt][0]=father[rt];for (int i=1;(1<<i)<=deep[rt];i++)Anst[rt][i]=Anst[Anst[rt][i-1]][i-1];}}int LCA(int a,int b){if (deep[a]>deep[b])swap(a,b);for (int i=deep[b]-deep[a],j=0;i>0;i>>=1,j++)if (i&1)b=Anst[b][j];if (a==b)return a;int k;for (k=0;(1<<k)<=deep[a];k++);for (;k>=0;k--)if ((1<<k)<=deep[a]&&Anst[a][k]!=Anst[b][k])a=Anst[a][k],b=Anst[b][k];return Anst[a][0];}bool check(int t){int total=0,Maxcost=0,Maxcut=0;memset(Nextsum,0,sizeof Nextsum);for (int i=1;i<=m;i++)if (q[i].cost>t){Maxcost=max(Maxcost,q[i].cost-t);total++;Nextsum[q[i].x]++;Nextsum[q[i].y]++;Nextsum[q[i].LCA]-=2;}for (int i=n;i>=1;i--)Nextsum[father[bh[i]]]+=Nextsum[bh[i]];for (int i=1;i<=n;i++)if (Nextsum[i]==total)Maxcut=max(Maxcut,fadis[i]);return Maxcost<=Maxcut;}int main(){scanf("%d%d",&n,&m);e.set();for (int i=1;i<n;i++){int a,b,c;read(a),read(b),read(c);e.add(a,b,c);e.add(b,a,c);}bhtot=0;deep[0]=-1,dis[1]=fadis[1]=0;Build_Tree(0,1);LCA_Prepare();for (int i=1;i<=m;i++){read(q[i].x),read(q[i].y);q[i].LCA=LCA(q[i].x,q[i].y);q[i].cost=dis[q[i].x]+dis[q[i].y]-dis[q[i].LCA]*2;}int le=0,ri=Inf,mid,ans=0;while (le<=ri){mid=(le+ri)>>1;if (check(mid))ri=mid-1,ans=mid;elsele=mid+1;}printf("%d",ans);return 0;}