leetcode 70. Climbing Stairs

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

这道题我一开始用的排列组合的思想，知道了1步台阶的个数 a 和2步台阶的个数 b，那么可以得到总个数c=a+b。然后这种情况就是组合题，c个台阶去取b（或者c个台阶去取a)，即C(c,b)。但是这种方法不行！！因为求C(n/k)的时候会有精度问题，如C(5,3)，如果令result为double类型，那么(5/3)*(4/2)*(3/1)由于是double*double*double，在double数量足够多时，会出现精度不准的问题，这个无法避免。而如果先求出被除数5*4*3，再求出除数3*2*1，最后再用被除数/除数，则会出现被除数太大而溢出的情况，即使把被除数换成long类型，当n为44时，依旧发生溢出。心累！

只好换其他方法了。

public int climbStairs(int n) {if(n == 1 || n == 2){return n;}int[] dp=new int[n+1];dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){//相当于在dp[i-1]的每个情况上加上1步//和在dp[i-2]的每个情况上加上2步dp[i]=dp[i-1]+dp[i-2];}return dp[n];}

这道题有solutions：https://leetcode.com/problems/climbing-stairs/solution/

Solution

---

Approach #1 Brute Force [Time Limit Exceeded]

Algorithm

In this brute force approach we take all possible step combinations i.e. 1 and 2, at every step. At every step we are calling the function $climbStairs$ for step $1$and $2$, and return the sum of returned values of both functions.

$climbStairs(i,n)=(i+1,n)+climbStairs(i+2,n)$, where $i$ defines the current step and $n$ defines the destination step.

Java

public class Solution {    public int climbStairs(int n) {        climb_Stairs(0, n);    }    public int climb_Stairs(int i, int n) {        if (i > n) {            return 0;        }        if (i == n) {            return 1;        }        return climb_Stairs(i + 1, n) + climb_Stairs(i + 2, n);    }}

Complexity Analysis

• Time complexity : O(2^n)O(2​n​​). Size of recursion tree will be 2^n2​n​​.

  Recursion tree for n=5 would be like this:

  

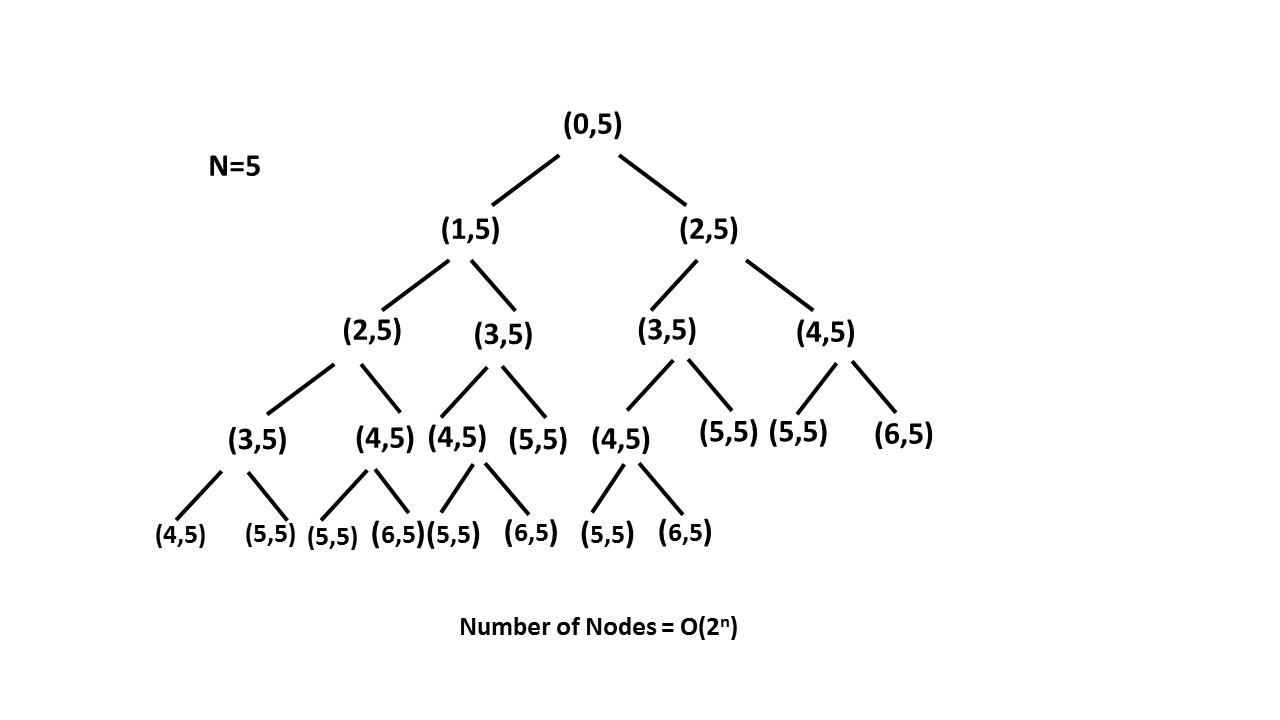
• Space complexity : $O(n)$. The depth of the recursion tree can go upto $n$.

---

Approach #2 Recursion with memorization [Accepted]

Java

public class Solution {    public int climbStairs(int n) {        int memo[] = new int[n + 1];        return climb_Stairs(0, n, memo);    }    public int climb_Stairs(int i, int n, int memo[]) {        if (i > n) {            return 0;        }        if (i == n) {            return 1;        }        if (memo[i] > 0) {            return memo[i];        }        memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);        return memo[i];    }}

Complexity Analysis

• Time complexity : $O(n)$. Size of recursion tree can go upto $n$.

• Space complexity : $O(n)$. The depth of recursion tree can go upto $n$.

---

Approach #3 Dynamic Programming [Accepted]

Algorithm

One can reach i^{th}i​th​​ step in one of the two ways:

1. Taking a single step from (i-1)^{th}(i−1)​th​​ step.

2. Taking a step of $2$ from (i-2)^{th}(i−2)​th​​ step.

$dp[i]=dp[i-1]+dp[i-2]$

Java

public class Solution {    public int climbStairs(int n) {        if (n == 1) {            return 1;        }        int[] dp = new int[n + 1];        dp[1] = 1;        dp[2] = 2;        for (int i = 3; i <= n; i++) {            dp[i] = dp[i - 1] + dp[i - 2];        }        return dp[n];    }}

Complexity Analysis

• Time complexity : $O(n)$. Single loop upto $n$.

• Space complexity : $O(n)$. $dp$ array of size $n$ is used.

---

Approach #4 Fibonacci Number [Accepted]:

Algorithm

In the above approach we have used $dp$ array where $dp[i]=dp[i-1]+dp[i-2]$. It can be easily analysed that $dp[i]$ is nothing but i^{th}i​th​​ fibonacci number.

$Fib(n)=Fib(n-1)+Fib(n-2)$

Now we just have to find n^{th}n​th​​ number of the fibonacci series having $1$ and $2$ their first and second term respectively i.e. $Fib(1)=1$ and $Fib(2)=2$.

Java

public class Solution {    public int climbStairs(int n) {        if (n == 1) {            return 1;        }        int first = 1;        int second = 2;        for (int i = 3; i <= n; i++) {            int third = first + second;            first = second;            second = third;        }        return second;    }}

Complexity Analysis

• Time complexity : $O(n)$. Single loop upto $n$ is required to calculate n^{th}n​th​​ fibonacci number.

• Space complexity : $O(1)$. Constant space is used.

---

Approach #6 Fibonacci Formula [Accepted]:

Algorithm

We can find n^{th}n​th​​ fibonacci number using this formula:

F_n = 1/\sqrt{5}\left[ \left(\frac{1+\sqrt{5}}{2}\right)^{n} - \left(\frac{1-\sqrt{5}}{2}\right)^{n} \right]F​n​​=1/√​5​​​[(​2​​1+√​5​​​​​)​n​​−(​2​​1−√​5​​​​​)​n​​]

For the given problem, the Fibonacci sequence is defined by F_0 = 1F​0​​=1, F_1= 1F​1​​=1, F_1= 2F​1​​=2, F_{n+2}= F_{n+1} + F_nF​n+2​​=F​n+1​​+F​n​​. A standard method of trying to solve such recursion formulas is assume F_nF​n​​ of the form F_n= a^nF​n​​=a​n​​. Then, of course, F_{n+1} = a^{n+1}F​n+1​​=a​n+1​​ and F_{n+2}= a^{n+2}F​n+2​​=a​n+2​​ so the equation becomes a^{n+2}= a^{n+1}+ a^na​n+2​​=a​n+1​​+a​n​​. If we divide the entire equation by an we arrive at a^2= a + 1a​2​​=a+1 or the quadratic equation

a^2 - a- 1= 0a​2​​−a−1=0.

Solving this by the quadratic formula, we get:

a=1/\sqrt{5}\left(\left(\frac{1\pm \sqrt{5}}{2}\right)\right)a=1/√​5​​​((​2​​1±√​5​​​​​)).

The general solution, thus takes the form:

F_n = A\left(\frac{1+\sqrt{5}}{2}\right)^{n} + B\left(\frac{1-\sqrt{5}}{2}\right)^{n}F​n​​=A(​2​​1+√​5​​​​​)​n​​+B(​2​​1−√​5​​​​​)​n​​

For $n=0$, we get $A+B=1$

For $n=1$, we get A\left(\frac{1+\sqrt{5}}{2}\right) + B\left(\frac{1-\sqrt{5}}{2}\right) = 1A(​2​​1+√​5​​​​​)+B(​2​​1−√​5​​​​​)=1

Solving the above equations, we get:

A = \left(\frac{1+\sqrt{5}}{2\sqrt{5}}\right), B = \left(\frac{1-\sqrt{5}}{2\sqrt{5}}\right)A=(​2√​5​​​​​1+√​5​​​​​),B=(​2√​5​​​​​1−√​5​​​​​)

Putting these values of $A$ and $B$ in the above general solution equation, we get:

F_n = 1/\sqrt{5}\left( \left(\frac{1+\sqrt{5}}{2}\right)^{n+1} - \left(\frac{1-\sqrt{5}}{2}\right)^{n+1} \right)

F​n​​=1/√​5​​​((​2​​1+√​5​​​​​)​n+1​​−(​2​​1−√​5​​​​​)​n+1​​)

Java

public class Solution {    public int climbStairs(int n) {        double sqrt5=Math.sqrt(5);        double fibn=Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1);        return (int)(fibn/sqrt5);    }}

Complexity Analysis

• Time complexity : $O(log(n))$. $pow$ method takes $log(n)$ time.

• Space complexity : $O(1)$. Constant space is used.