隐马尔科夫模型(二)
来源:互联网 发布:淘宝二手ps4主机能买吗 编辑:程序博客网 时间:2024/05/20 21:48
作者:henry
链接:https://www.zhihu.com/question/20962240/answer/64187492
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
链接:https://www.zhihu.com/question/20962240/answer/64187492
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
隐形马尔可夫模型,英文是 Hidden Markov Models,所以以下就简称 HMM。
既是马尔可夫模型,就一定存在马尔可夫链,该马尔可夫链服从马尔可夫性质:即无记忆性。也就是说,这一时刻的状态,受且只受前一时刻的影响,而不受更往前时刻的状态的影响。
在这里我们仍然使用非常简单的天气模型来做说明。
<img src="https://pic4.zhimg.com/648a55725e67d718d97d6a475891d70b_b.png" data-rawwidth="600" data-rawheight="566" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic4.zhimg.com/648a55725e67d718d97d6a475891d70b_r.png">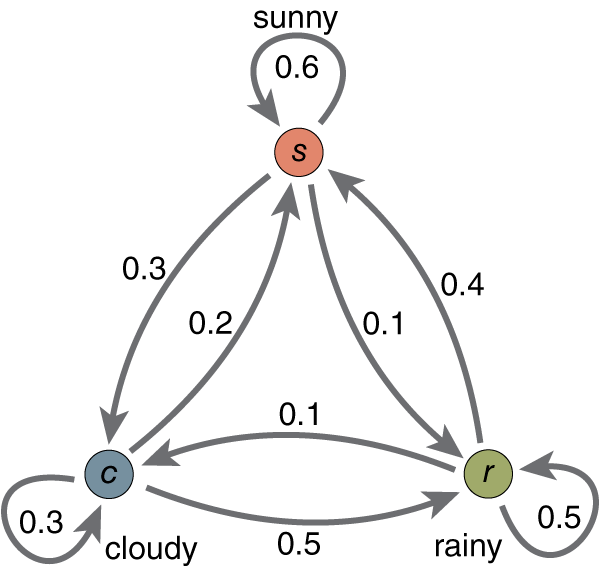
在这个马尔可夫模型中,存在三个状态,Sunny, Rainy, Cloudy,同时图片上标的是各个状态间的转移概率(如果不明白什么是转移概率,那建议先去学习什么是马尔可夫再来看HMM)。
现在我们要说明什么是 HMM。既是隐形,说明这些状态是观测不到的,相应的,我们可以通过其他方式来『猜测』或是『推断』这些状态,这也是 HMM 需要解决的问题之一。
举个例子,我女朋友现在在北京工作,而我还在法国读书。每天下班之后,她会根据天气情况有相应的活动:或是去商场购物,或是去公园散步,或是回家收拾房间。我们有时候会通电话,她会告诉我她这几天做了什么,而闲着没事的我呢,则要通过她的行为猜测这几天对应的天气最有可能是什么样子的。
以上就是一个简单的 HMM,天气状况属于状态序列,而她的行为则属于观测序列。天气状况的转换是一个马尔可夫序列。而根据天气的不同,有相对应的概率产生不同的行为。在这里,为了简化,把天气情况简单归结为晴天和雨天两种情况。雨天,她选择去散步,购物,收拾的概率分别是0.1,0.4,0.5, 而如果是晴天,她选择去散步,购物,收拾的概率分别是0.6,0.3,0.1。而天气的转换情况如下:这一天下雨,则下一天依然下雨的概率是0.7,而转换成晴天的概率是0.3;这一天是晴天,则下一天依然是晴天的概率是0.6,而转换成雨天的概率是0.4. 同时还存在一个初始概率,也就是第一天下雨的概率是0.6, 晴天的概率是0.4.
<img src="https://pic4.zhimg.com/792e033ff9b0418b3b6c9bbaef30fd83_b.png" data-rawwidth="623" data-rawheight="477" class="origin_image zh-lightbox-thumb" width="623" data-original="https://pic4.zhimg.com/792e033ff9b0418b3b6c9bbaef30fd83_r.png">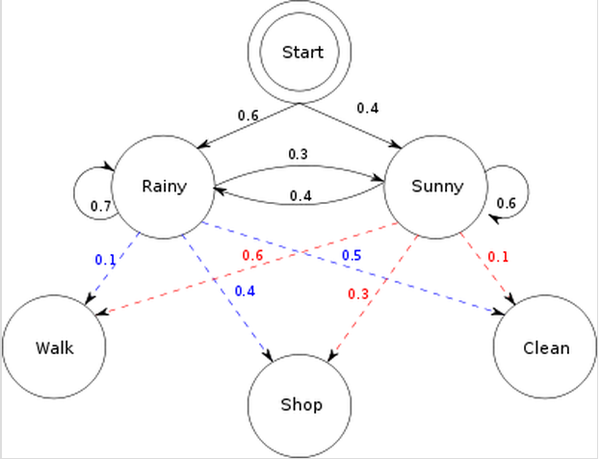
根据以上的信息,我们得到了 HMM的一些基本要素:初始概率分布 π,状态转移矩阵 A,观测量的概率分布 B,同时有两个状态,三种可能的观测值。
现在,重点是要了解并解决HMM 的三个问题。
问题1,已知整个模型,我女朋友告诉我,连续三天,她下班后做的事情分别是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
问题2,同样知晓这个模型,同样是这三件事,我女朋友要我猜,这三天她下班后北京的天气是怎么样的。这三天怎么样的天气才最有可能让她做这样的事情。
问题3,最复杂的,我女朋友只告诉我这三天她分别做了这三件事,而其他什么信息我都没有。她要我建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况她选择做某事的概率分布。(惨绝人寰)
而要解决这些问题,伟大的大师们分别找出了对应的算法。问题一,Forward Algorithm,向前算法,或者 Backward Algo,向后算法。 问题二,Viterbi Algo,维特比算法。问题三,Baum-Welch Algo,鲍姆-韦尔奇算法(中文好绕口)。
尽管例子有些荒谬(天气情况要复杂的多,而且不太可能满足马尔可夫性质;同时,女朋友要做什么往往由心情决定而不由天气决定。而从问题一来看,一定是天数越多,这个概率就会越低;从问题三来看,观察到的行为越多,模型才能更准确一些),但是应该已经简单却又详尽地解释了什么是 HMM。如果只是想了解个大概,到此为止。
===========================我是分割线====================================
分割线以下的,就是具体如何解决这三大问题。需要数学基础,概率基础。
问题1的解决1:遍历算法。
要计算产生这一系列行为的概率,那我们把每一种天气情况下产生这些行为都罗列出来,那每种情况的和就是这个概率。有三天,每天有两种可能的天气情况,则总共有 种情况.
种情况.
举例其中一种情况 : P(下雨,下雨,下雨,散步,购物,收拾)=P(第一天下雨)P(第一天下雨去散步)P(第二天接着下雨)P(下雨去购物)P(第三天还下雨)P(下雨回家收拾)=0.6X0.1X0.7X0.4X0.7X0.5=0.00588
当然,这里面的 P(第二天接着下雨)当然是已知第一天下雨的情况下,第二天下雨的概率,为0.7.
将八种情况相加可得,三天的行为为{散步,购物,收拾}的可能性为0.033612. 看似简单易计算,但是一旦观察序列变长,计算量就会非常庞大( 的复杂度,T 为观测序列的长度)。
的复杂度,T 为观测序列的长度)。
问题1 的解决2:向前算法。
先计算 t=1时刻,发生『散步』一行为的概率,如果下雨,则为 P(散步,下雨)=P(第一天下雨)X P(散步 | 下雨)=0.6X0.1=0.06;晴天,P(散步,晴天)=0.4X0.6=0.24
t=2 时刻,发生『购物』的概率,当然,这个概率可以从 t=1 时刻计算而来。
如果t=2下雨,则 P(第一天散步,第二天购物, 第二天下雨)= 【P(第一天散步,第一天下雨)X P(第二天下雨 | 第一天下雨)+P(第一天散步,第一天晴天)X P(第二天下雨 | 第一天晴天)】X P(第二天购物 | 第二天下雨)=【0.06X0.7+0.24X0.3】X0.4=0.0552
如果 t=2晴天,则 P(第一天散步,第二天购物,第二天晴天)=0.0486 (同理可得,请自行推理)
如果 t=3,下雨,则 P(第一天散步,第二天购物,第三天收拾,第三天下雨)=【P(第一天散步,第二天购物,第二天下雨)X P(第三天下雨 | 第二天下雨)+ P(第一天散步,第二天购物,第二天天晴)X P(第三天下雨 | 第二天天晴)】X P(第三天收拾 | 第三天下雨)=【0.0552X0.7+0.0486X0.4】X0.5= 0.02904
如果t=3,晴天,则 P(第一天散步,第二天购物,第三天收拾,第三天晴天)= 0.004572
那么 P(第一天散步,第二天购物,第三天收拾),这一概率则是第三天,下雨和晴天两种情况的概率和。0.02904+0.004572=0.033612.
以上例子可以看出,向前算法计算了每个时间点时,每个状态的发生观测序列的概率,看似繁杂,但在 T 变大时,复杂度会大大降低。
<img src="https://pic4.zhimg.com/489523ae4ffe659de5f7c73c074cef6f_b.png" data-rawwidth="340" data-rawheight="269" class="content_image" width="340">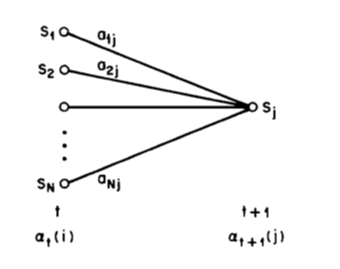
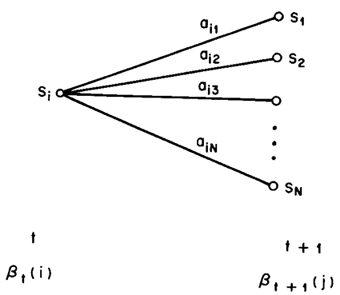
问题1的解决3:向后算法
顾名思义,向前算法是在时间 t=1的时候,一步一步往前计算。而相反的,向后算法则是倒退着,从最后一个状态开始,慢慢往后推。
初始化: (第一次使用知乎的公式编辑,还蛮靠谱的嘛)
(第一次使用知乎的公式编辑,还蛮靠谱的嘛)

递推:
=0,.7x0.5x1+0.3x0.1x1=0.38
其中第一项则是转移概率,第二天下雨转到第三天下雨的概率为0.7;第二项则是观测概率,第三天下雨的状况下,在家收拾的概率为0.5;第三项就是我们定义的向后变量(backward variable)。
同理推得
结束:P(散步,购物,收拾) = =0.6×0.1×0.1298+0.4×0.6×0.1076
=0.6×0.1×0.1298+0.4×0.6×0.1076
![\delta_2(Rainy)=max[\delta_1(R)\times a_{R\to R},\delta_1(S)\times a_{S\to R}]\times b_R(O_2=Shop)=0.0384](https://www.zhihu.com/equation?tex=%5Cdelta_2%28Rainy%29%3Dmax%5B%5Cdelta_1%28R%29%5Ctimes+a_%7BR%5Cto+R%7D%2C%5Cdelta_1%28S%29%5Ctimes+a_%7BS%5Cto+R%7D%5D%5Ctimes+b_R%28O_2%3DShop%29%3D0.0384)
![\phi_2(Rainy)=\arg\max[\delta_1(R)\times a_{R\to R},\delta_1(S)\times a_{S\to R}]=Sunny](https://www.zhihu.com/equation?tex=%5Cphi_2%28Rainy%29%3D%5Carg%5Cmax%5B%5Cdelta_1%28R%29%5Ctimes+a_%7BR%5Cto+R%7D%2C%5Cdelta_1%28S%29%5Ctimes+a_%7BS%5Cto+R%7D%5D%3DSunny)
也就是说,第一天是晴天的可能性更大。
同样地,可以推得,
结束:比较 的大小,发现前者较大,则最后一天的状态最有可能是 下雨天。
的大小,发现前者较大,则最后一天的状态最有可能是 下雨天。
回推:根据 可知,到达第三天下雨这一状态,最有可能是第二天也下雨,再根据
可知,到达第三天下雨这一状态,最有可能是第二天也下雨,再根据 可知,到达第二天下雨这一状态,最有可能是第一天是晴天。
可知,到达第二天下雨这一状态,最有可能是第一天是晴天。
由此,我们得到了最佳路径,即,晴天,雨天,雨天。
既是马尔可夫模型,就一定存在马尔可夫链,该马尔可夫链服从马尔可夫性质:即无记忆性。也就是说,这一时刻的状态,受且只受前一时刻的影响,而不受更往前时刻的状态的影响。
在这里我们仍然使用非常简单的天气模型来做说明。
<img src="https://pic4.zhimg.com/648a55725e67d718d97d6a475891d70b_b.png" data-rawwidth="600" data-rawheight="566" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic4.zhimg.com/648a55725e67d718d97d6a475891d70b_r.png">

在这个马尔可夫模型中,存在三个状态,Sunny, Rainy, Cloudy,同时图片上标的是各个状态间的转移概率(如果不明白什么是转移概率,那建议先去学习什么是马尔可夫再来看HMM)。
现在我们要说明什么是 HMM。既是隐形,说明这些状态是观测不到的,相应的,我们可以通过其他方式来『猜测』或是『推断』这些状态,这也是 HMM 需要解决的问题之一。
举个例子,我女朋友现在在北京工作,而我还在法国读书。每天下班之后,她会根据天气情况有相应的活动:或是去商场购物,或是去公园散步,或是回家收拾房间。我们有时候会通电话,她会告诉我她这几天做了什么,而闲着没事的我呢,则要通过她的行为猜测这几天对应的天气最有可能是什么样子的。
以上就是一个简单的 HMM,天气状况属于状态序列,而她的行为则属于观测序列。天气状况的转换是一个马尔可夫序列。而根据天气的不同,有相对应的概率产生不同的行为。在这里,为了简化,把天气情况简单归结为晴天和雨天两种情况。雨天,她选择去散步,购物,收拾的概率分别是0.1,0.4,0.5, 而如果是晴天,她选择去散步,购物,收拾的概率分别是0.6,0.3,0.1。而天气的转换情况如下:这一天下雨,则下一天依然下雨的概率是0.7,而转换成晴天的概率是0.3;这一天是晴天,则下一天依然是晴天的概率是0.6,而转换成雨天的概率是0.4. 同时还存在一个初始概率,也就是第一天下雨的概率是0.6, 晴天的概率是0.4.
<img src="https://pic4.zhimg.com/792e033ff9b0418b3b6c9bbaef30fd83_b.png" data-rawwidth="623" data-rawheight="477" class="origin_image zh-lightbox-thumb" width="623" data-original="https://pic4.zhimg.com/792e033ff9b0418b3b6c9bbaef30fd83_r.png">

根据以上的信息,我们得到了 HMM的一些基本要素:初始概率分布 π,状态转移矩阵 A,观测量的概率分布 B,同时有两个状态,三种可能的观测值。
现在,重点是要了解并解决HMM 的三个问题。
问题1,已知整个模型,我女朋友告诉我,连续三天,她下班后做的事情分别是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
问题2,同样知晓这个模型,同样是这三件事,我女朋友要我猜,这三天她下班后北京的天气是怎么样的。这三天怎么样的天气才最有可能让她做这样的事情。
问题3,最复杂的,我女朋友只告诉我这三天她分别做了这三件事,而其他什么信息我都没有。她要我建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况她选择做某事的概率分布。(惨绝人寰)
而要解决这些问题,伟大的大师们分别找出了对应的算法。问题一,Forward Algorithm,向前算法,或者 Backward Algo,向后算法。 问题二,Viterbi Algo,维特比算法。问题三,Baum-Welch Algo,鲍姆-韦尔奇算法(中文好绕口)。
尽管例子有些荒谬(天气情况要复杂的多,而且不太可能满足马尔可夫性质;同时,女朋友要做什么往往由心情决定而不由天气决定。而从问题一来看,一定是天数越多,这个概率就会越低;从问题三来看,观察到的行为越多,模型才能更准确一些),但是应该已经简单却又详尽地解释了什么是 HMM。如果只是想了解个大概,到此为止。
===========================我是分割线====================================
分割线以下的,就是具体如何解决这三大问题。需要数学基础,概率基础。
问题1的解决1:遍历算法。
要计算产生这一系列行为的概率,那我们把每一种天气情况下产生这些行为都罗列出来,那每种情况的和就是这个概率。有三天,每天有两种可能的天气情况,则总共有
举例其中一种情况 : P(下雨,下雨,下雨,散步,购物,收拾)=P(第一天下雨)P(第一天下雨去散步)P(第二天接着下雨)P(下雨去购物)P(第三天还下雨)P(下雨回家收拾)=0.6X0.1X0.7X0.4X0.7X0.5=0.00588
当然,这里面的 P(第二天接着下雨)当然是已知第一天下雨的情况下,第二天下雨的概率,为0.7.
将八种情况相加可得,三天的行为为{散步,购物,收拾}的可能性为0.033612. 看似简单易计算,但是一旦观察序列变长,计算量就会非常庞大(
问题1 的解决2:向前算法。
先计算 t=1时刻,发生『散步』一行为的概率,如果下雨,则为 P(散步,下雨)=P(第一天下雨)X P(散步 | 下雨)=0.6X0.1=0.06;晴天,P(散步,晴天)=0.4X0.6=0.24
t=2 时刻,发生『购物』的概率,当然,这个概率可以从 t=1 时刻计算而来。
如果t=2下雨,则 P(第一天散步,第二天购物, 第二天下雨)= 【P(第一天散步,第一天下雨)X P(第二天下雨 | 第一天下雨)+P(第一天散步,第一天晴天)X P(第二天下雨 | 第一天晴天)】X P(第二天购物 | 第二天下雨)=【0.06X0.7+0.24X0.3】X0.4=0.0552
如果 t=2晴天,则 P(第一天散步,第二天购物,第二天晴天)=0.0486 (同理可得,请自行推理)
如果 t=3,下雨,则 P(第一天散步,第二天购物,第三天收拾,第三天下雨)=【P(第一天散步,第二天购物,第二天下雨)X P(第三天下雨 | 第二天下雨)+ P(第一天散步,第二天购物,第二天天晴)X P(第三天下雨 | 第二天天晴)】X P(第三天收拾 | 第三天下雨)=【0.0552X0.7+0.0486X0.4】X0.5= 0.02904
如果t=3,晴天,则 P(第一天散步,第二天购物,第三天收拾,第三天晴天)= 0.004572
那么 P(第一天散步,第二天购物,第三天收拾),这一概率则是第三天,下雨和晴天两种情况的概率和。0.02904+0.004572=0.033612.
以上例子可以看出,向前算法计算了每个时间点时,每个状态的发生观测序列的概率,看似繁杂,但在 T 变大时,复杂度会大大降低。
<img src="https://pic4.zhimg.com/489523ae4ffe659de5f7c73c074cef6f_b.png" data-rawwidth="340" data-rawheight="269" class="content_image" width="340">

问题1的解决3:向后算法
顾名思义,向前算法是在时间 t=1的时候,一步一步往前计算。而相反的,向后算法则是倒退着,从最后一个状态开始,慢慢往后推。
初始化:
递推:
=0,.7x0.5x1+0.3x0.1x1=0.38
其中第一项则是转移概率,第二天下雨转到第三天下雨的概率为0.7;第二项则是观测概率,第三天下雨的状况下,在家收拾的概率为0.5;第三项就是我们定义的向后变量(backward variable)。
同理推得
结束:P(散步,购物,收拾) =
=0.033612
<img src="https://pic3.zhimg.com/1a89bf925b4c1af2cc17416764d1d60e_b.png" data-rawwidth="340" data-rawheight="295" class="content_image" width="340">
三种算法的答案是一致的。
问题2的解决:维特比算法
维特比算法致力于寻找一条最佳路径,以便能最好地解释观测到的序列。
初始化:
初始路径:
递推,当然是要找出概率比较大的那条路径。
那么,到达第二天下雨这一状态的最佳路径,应该是:
也就是说,第一天是晴天的可能性更大。
同样地,可以推得,
结束:比较
回推:根据
由此,我们得到了最佳路径,即,晴天,雨天,雨天。
阅读全文
0 0
- 隐马尔科夫模型(二)
- 隐马尔科夫模型(二)
- 隐马尔科夫模型(二)
- 隐马尔科夫模型HMM自学(二)
- 隐马尔科夫模型HMM学习(二)
- HMM(隐马尔科夫模型)学习二
- 隐马尔科夫模型的介绍(二)
- 隐马尔科夫模型-----二
- 服务器模型(二)
- 网络模型(二)
- 设计模型之观察者模型(二)
- 几种频域滤波模型(二)
- C++对象模型(二)
- c++ 对象模型(二)
- 【Html】流动模型(二)
- C++ 对象模型(二)
- java内存模型(二)
- actor 模型原理 (二)
- OKHTTP和Retrofit
- libvirt api 虚拟机动态迁移代码示例(非共享存储)
- ORACLE索引原理
- 边框回归(Bounding Box Regression)详解
- js得到连两个时间段之间所有的年-月 获取当前日期 格式化日期 根据指定日期得到该日期该月份的最后一天
- 隐马尔科夫模型(二)
- C++实现WEB功能方法总结
- cookie和session的区别
- 发现了一个好用的WEB项目打印控件--四方打印
- 阿里、百度等多家公司Java面试记录与总结
- C++调用Python模块
- Hadoop MapReduce执行过程中map和reduce执行过程
- 算法题/数组中出现次数超过一半的数字
- Java的反射


