2017 ACM-ICPC 亚洲区（南宁赛区）网络赛： G. Finding the Radius for an Inserted Circle（笛卡尔定理）

来源：互联网发布：c语言visit函数编辑：程序博客网时间：2024/05/20 09:25

Three circles $C_{a}$ , $C_{b}$ , and $C_{c}$ , all with radius $R$ and tangent to each other, are located in two-dimensional space as shown in Figure $1$ . A smaller circle $C_{1}$ with radius $R_{1}$ ( $R_{1}<R$ ) is then inserted into the blank area bounded by $C_{a}$ , $C_{b}$ , and $C_{c}$ so that $C_{1}$ is tangent to the three outer circles, $C_{a}$ , $C_{b}$ , and $C_{c}$ . Now, we keep inserting a number of smaller and smaller circles $C_{k}\ (2 \leq k \leq N)$ with the corresponding radius $R_{k}$ into the blank area bounded by $C_{a}$ , $C_{c}$ and $C_{k-1}$ $\leq k \leq N)$ , so that every time when the insertion occurs, the inserted circle $C_{k}$ is always tangent to the three outer circles $C_{a}$ , $C_{c}$ and $C_{k-1}$ , as shown in Figure $1$

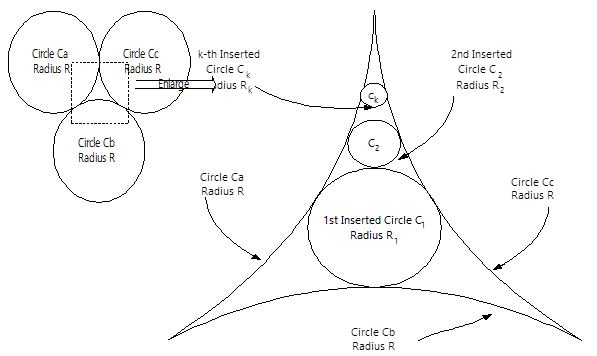
Figure 1.

(Left) Inserting a smaller circle $C_{1}$ into a blank area bounded by the circle $C_{a}$ , $C_{b}$ and $C_{c}$ .

(Right) An enlarged view of inserting a smaller and smaller circle $C_{k}$ into a blank area bounded by $C_{a}$ , $C_{c}$ and $C_{k-1}$ ( $\leq k \leq N$ ), so that the inserted circle $C_{k}$ is always tangent to the three outer circles, $C_{a}$ , $C_{c}$ , and $C_{k-1}$ .

Now, given the parameters $R$ and $k$ , please write a program to calculate the value of $R_{k}$ , i.e., the radius of the $k - t h$ inserted circle. Please note that since the value of $R_k$ may not be an integer, you only need to report the integer part of $R_{k}$ . For example, if you find that $R_{k}$ = $1259.8998$ for some $k$ , then the answer you should report is $1259$ .

Another example, if $R_{k}$ = $39.1029$ for some $k$ , then the answer you should report is $39$ .

Assume that the total number of the inserted circles is no more than $10$ , i.e., $\leq 10$ . Furthermore, you may assume $\pi = 3.14159$ . The range of each parameter is as below:

$\leq k \leq N$ , and $10^{4} \leq R \leq 10^{7}$ .

Input Format

Contains $l + 3$ lines.

Line $1$ : $l$ ----------------- the number of test cases, $l$ is an integer.

Line $2$ : $R$ ---------------- $R$ is a an integer followed by a decimal point,then followed by a digit.

Line $3$ : $k$ ---------------- test case # $1$ , $k$ is an integer.

$\ldots$

Line $i + 2$ : $k$ ----------------- test case # $i$ .

$\ldots$

Line $l + 2$ : $k$ ------------ test case # $l$ .

Line $l + 3$ : $- 1$ ---------- a constant $- 1$ representing the end of the input file.

Output Format

Contains $l$ lines.

Line $1$ : $k$ $R_{k}$ ----------------output for the value of $k$ and $R_{k}$ at the test case # $1$ , each of which should be separated by a blank.

$\ldots$

Line $i$ : $k$ $R_{k}$ ----------------output for $k$ and the value of $R_{k}$ at the test case # $i$ , each of which should be separated by a blank.

Line $l$ : $k$ $R_{k}$ ----------------output for $k$ and the value of $R_{k}$ at the test case # $l$ , each of which should be separated by a blank.

样例输入

1152973.61-1

样例输出

1 23665

思路：

(1)笛卡尔定理

定义一个圆的曲率k=±1r，其中r是其半径。
若平面有两两相切，且有6个独立切点的四个圆，设其曲率为k1,k2,k3,k4（若该圆与其他圆均外切，则曲率取正，否则取负）则其满足性质：

(k 1 + k 2 + k 3 + k 4) 2 = 2 (k 21 + k 22 + k 23 + k 24)

根据这个定理，我们就可以类似迭代的方式，不断往后递推求解。

#include<bits/stdc++.h>using namespace std;const double PI=3.14159;int main(){    int T,n;    double R;    while(scanf("%d",&T)!=EOF&&T!=-1)    {        scanf("%lf",&R);        while(T--)        {            scanf("%d",&n);            double k1=1/R,k2=1/R,k3=1/R;            double ans;            for(int i=0;i<n;i++)            {                double B=-2*(k1+k2+k3);                double C=-(k1+k2+k3)*(k1+k2+k3)+2*(k1*k1+k2*k2+k3*k3);                double D=B*B-4*C;                double k4=max((-B-sqrt(D))/2,(-B+sqrt(D))/2);                ans=1/k4;                k3=k4;            }            printf("%d %0.lf\n",n,floor(ans));        }    }    return 0;}

阅读全文

1 0