2017 ACM-ICPC 亚洲区（南宁赛区）网络赛 G. Finding the Radius for an Inserted Circle(计算几何，二分)

Finding the Radius for an Inserted Circle

Three circles C_{a}C​a​​, C_{b}C​b​​, and C_{c}C​c​​, all with radius $R$ and tangent to each other, are located in two-dimensional space as shown in Figure $1$. A smaller circle C_{1}C​1​​ with radius R_{1}R​1​​ (R_{1}<RR​1​​<R) is then inserted into the blank area bounded by C_{a}C​a​​, C_{b}C​b​​, and C_{c}C​c​​ so that C_{1}C​1​​ is tangent to the three outer circles, C_{a}C​a​​, C_{b}C​b​​, and C_{c}C​c​​. Now, we keep inserting a number of smaller and smaller circles C_{k}\ (2 \leq k \leq N)C​k​​ (2≤k≤N) with the corresponding radius R_{k}R​k​​ into the blank area bounded by C_{a}C​a​​, C_{c}C​c​​ and C_{k-1}C​k−1​​ $(2\le k\le N)$, so that every time when the insertion occurs, the inserted circle C_{k}C​k​​ is always tangent to the three outer circles C_{a}C​a​​, C_{c}C​c​​ and C_{k-1}C​k−1​​, as shown in Figure $1$

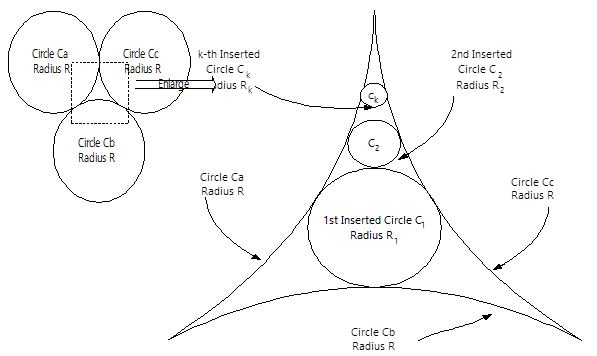
Figure 1.

(Left) Inserting a smaller circle C_{1}C​1​​ into a blank area bounded by the circle C_{a}C​a​​, C_{b}C​b​​ and C_{c}C​c​​.

(Right) An enlarged view of inserting a smaller and smaller circle C_{k}C​k​​ into a blank area bounded by C_{a}C​a​​, C_{c}C​c​​ and C_{k-1}C​k−1​​ ($2\le k\le N$), so that the inserted circle C_{k}C​k​​ is always tangent to the three outer circles, C_{a}C​a​​, C_{c}C​c​​, and C_{k-1}C​k−1​​.

Now, given the parameters $R$ and $k$, please write a program to calculate the value of R_{k}R​k​​, i.e., the radius of the $k-th$ inserted circle. Please note that since the value of R_kR​k​​ may not be an integer, you only need to report theinteger part of R_{k}R​k​​. For example, if you find that R_{k}R​k​​ = $1259.8998$ for some $k$, then the answer you should report is $1259$.

Another example, if R_{k}R​k​​ = $39.1029$ for some $k$, then the answer you should report is $39$.

Assume that the total number of the inserted circles is no more than $10$, i.e., $N\le 10$. Furthermore, you may assume $\pi =3.14159$. The range of each parameter is as below:

$1\le k\le N$, and 10^{4} \leq R \leq 10^{7}10​4​​≤R≤10​7​​.

Input Format

Contains $l+3$ lines.

Line $1$: $l$ ----------------- the number of test cases, $l$ is an integer.

Line $2$: $R$ ---------------- $R$ is a an integer followed by a decimal point,then followed by a digit.

Line $3$: $k$ ---------------- test case #$1$, $k$ is an integer.

$\dots$

Line $i+2$: $k$ ----------------- test case # $i$.

$\dots$

Line $l+2$: $k$ ------------ test case #$l$.

Line $l+3$: $-1$ ---------- a constant $-1$ representing the end of the input file.

Output Format

Contains $l$ lines.

Line $1$: $k$ R_{k}R​k​​ ----------------output for the value of $k$ and R_{k}R​k​​ at the test case #$1$, each of which should be separated by a blank.

$\dots$

Line $i$: $k$ R_{k}R​k​​ ----------------output for $k$ and the value of R_{k}R​k​​ at the test case # $i$, each of which should be separated by a blank.

Line $l$: $k$ R_{k}R​k​​ ----------------output for $k$ and the value ofR_{k}R​k​​ at the test case # $l$, each of which should be separated by a blank.

样例输入

1152973.61-1

样例输出

1 23665

题意：这道题就是给你三个一模一样的圆，左边一个右边一个下面一个，三个圆两两相切，然后在这三个圆中间的地方找一个小圆，要求这个小圆与这三个大圆相切，这被称为一次操作，然后第二次操作的时候，就把下面的大圆替换成那个小圆，然后从这两个大圆和一个小圆中间再找一个更小的圆也与它们相切，最后问你经过k次操作后那个小圆的半径是多少。

思路：我们可以把三个圆的圆心两两相连，连成一个三角形，再把三个圆心与中间的小圆心相连，假设左右两个大圆的半径为R，下面的圆半径为r，中间的小圆半径为s，那么就可以转化成下图。

红色的边都是已知长度的，并且长度都在图中标记了出来，因为相切，所以两圆心的距离等于两圆半径之和。

那么我们可以对图中的蓝色边做文章，蓝色边的长度可以等于sqrt((R+s)^2-R^2)，也可以等于sqrt((R+r)^2-R^2)-r-s。这样我们让这两个等式相等，就可以通过R和r求出s了，不过这个方程组里有根号，不是很好解，所以我们可以用二分的方法去寻找方程的解。s求出来后我们就完成了一次操作，然后把s的值赋给r，我们就可以进行第二次操作了。

#include <iostream>  #include <cstdio>  #include <cstring>  #include <string>  #include <cstdlib>  #include <cmath>  #include <vector>  #include <queue>  #include <map>  #include <algorithm>  #include <set>  #include <functional>  using namespace std;typedef long long LL;typedef unsigned long long ULL;const int INF = 1e9 + 5;const int MAXN = 100000007;const int MOD = 1e9 + 7;const double eps = 1e-8;const double PI = acos(-1.0);LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); }double R,r;double get(double x){return sqrt(x*x + 2 * R*x) + x;}double find(double r)//二分查找{int k = 200;double l=0, rr=1e7, m;double aim = sqrt((R + r)*(R + r) - R*R) - r;while (k--){m = (l + rr) / 2;if (get(m) - aim > eps)rr = m;elsel = m;}return m;}int main(){int T;int k;scanf("%d", &T);scanf("%lf", &R);while (T--){scanf("%d", &k);r = R;for (int i = 1; i <= k; i++)r = find(r);printf("%d %d\n", k, (int)r);}scanf("%d", &k);}