Codeforces Round #439 (Div. 2) C. The Intriguing Obsession dp

C. The Intriguing Obsession

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of a, b and c distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 1. For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998 244 353. Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

Input

The first and only line of input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 5 000) — the number of islands in the red, blue and purple clusters, respectively.

Output

Output one line containing an integer — the number of different ways to build bridges, modulo 998 244 353.

Examples

input

1 1 1

output

8

input

1 2 2

output

63

input

1 3 5

output

3264

input

6 2 9

output

813023575

Note

In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 23 = 8.

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

题意：有三个集合，分别有a，b，c个元素，同一集合的元素之间的最短路要大于等于3或者不能到达，任意两个元素都可以建边，问有多少种满足条件的建边方式。

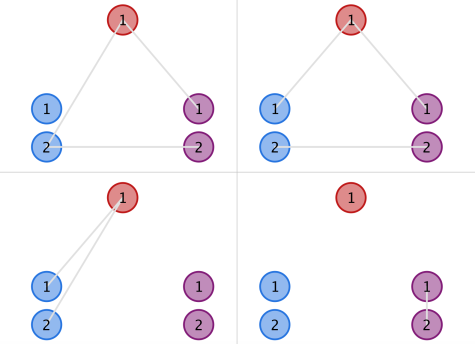
思路：讲道理，这题挺难想的怎么这么多人会，通过一番画图，我们可以观察到集合1和集合2的边并不影响集合2和集合3的边，也不影响集合1和集合3的边，也就是每一对集合的边都是独立的，所以只要求出每一对集合的可能，再乘起来就好了。。一对集合的答案可以通过dp求出，有转移方程：dp[i][j]=dp[i][j-1]+dp[i-1][j-1]*i。下面给代码：

#include<set>#include<map>#include<ctime>#include<cmath>#include<stack>#include<queue>#include<cstdio>#include<string>#include<cstring>#include<iostream>#include<algorithm>#include<functional>typedef long long LL;using namespace std;#define inf 0x3f3f3f3f#define maxn 5005typedef long long LL;LL dp[maxn][maxn];const LL mod = 998244353;int main(){int a, b, c;scanf("%d%d%d", &a, &b, &c);for (int i = 0; i <= 5000; i++)for (int j = 0; j <= 5000; j++){if (j){dp[i][j] += dp[i][j - 1];dp[i][j] %= mod;if (i){dp[i][j] += i*dp[i - 1][j - 1];dp[i][j] %= mod;}}elsedp[i][j] = 1;}printf("%lld\n", (dp[a][b] * dp[a][c] % mod)*dp[b][c] % mod);}