8. 机器学习基石-How can Machine Learn?

How can Machine Learn? - Logistic Regression

---

• How can Machine Learn? - Logistic Regression
  
  • 1. Introduction of Logistic Regression
  • 2. Comparison of Linear Regression, Logistic Classification and Logistic Regression
  • 3. Error Measurement of Logistic Regression - cross-entropy error
  • 4. Gradient of Logistic Regression Error
  • 5. Use Gradient Descent to Minimize the Error of Logistic Regression
  • 6. Choose Step Length for Gradient Descent
  • 7. Stochastic Gradient Descent - Another Approach of Gradient Descent
• Summary
• Reference

这一节讨论与 Linear Regression 非常类似的Logistic Regression

1. Introduction of Logistic Regression

使用二元分类分析心脏病复发问题，其输出空间只含有两项{+1，-1}，分别表示复发和不发复发。在含有噪音的情况下，目标函数f可以使用目标分布P来表示，如公式（1）所示

f(x)=sign(P(+1|x)−12)∈{+1,−1}(1)

但是实际情况，医生往往不会直接告诉病人说是否会心脏病复发，而是用概率，例如说有80%的可能性会复发，此种情况被称为软二元分类（soft binary classification），目标函数f的表达如公式（2）所示，其输出以概率的形式，在0~1之间。

f(x)=P(+1|x)∈[+1,−1](2)

但是病人的病历里面不可能记录以前有多少多少的几率复发/不复发，而是真实的记录病人是否复发。所以概率的情况来说，复发/不复发的情况就像是噪音了(因为偏离中间的概率值大)，所以我们把实际的训练数据看成是含有噪音的理想训练数据。这种问题如何求解呢？我们可以通过输入各属性 x=(x0,x1,x2,...,xn) 的加权总分数（weighted scores），如公式（3）所示

s=∑i=0nwixi=wTx(3)

这里的s的值不在 0~1之间，所以我们还需要将他进行归一化处理，那就可以使用Logistic Regression。函数用表示 θ(s)，叫做Logistic Function 或者 Sigmoid Function，如公式（4）所示。分数s越大风险越高，分数s越小风险越低。假设函数h如公式(5)所示，函数曲线的示意图如图一所示。

θ(s)=ee+ez=11+e−z(4)

h(x)=θ(wTx)=11+e−wTx(5)

图一 Logistic Curve ^[1]

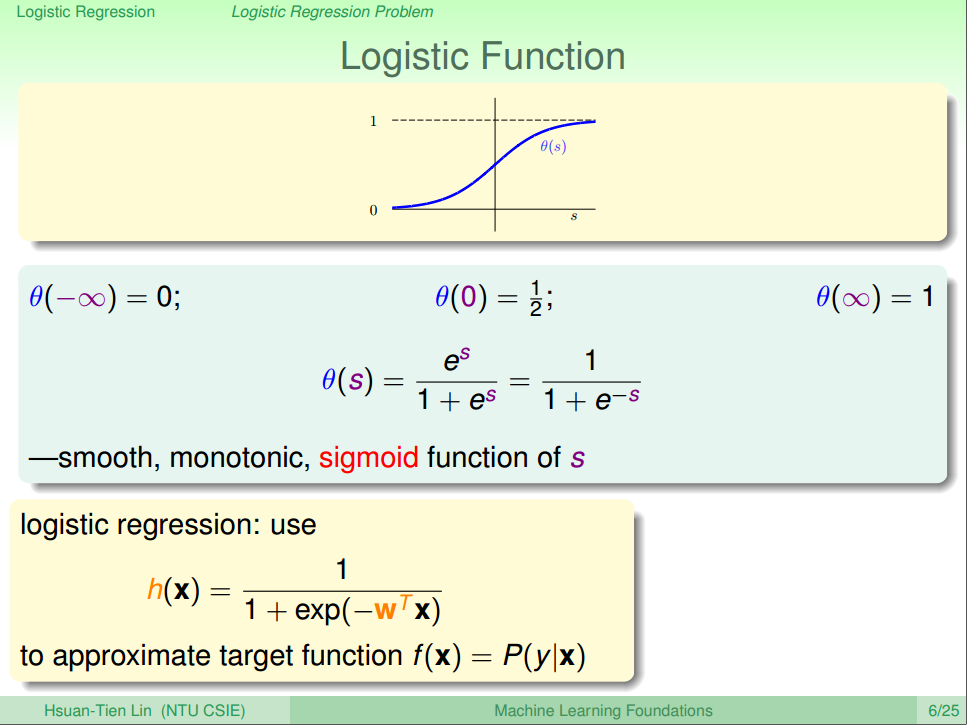
观察函数的图形，该函数是一个平滑（处处可微分），单调（monotonic）的S形（sigmoid）函数，因此又被称为sigmoid函数。

Logistic Regression 是当前业界比较常用的机器学习方法，用于估计某种事物的可能性，应用场合如：广告预测，购物推荐，患病可能性判断等。 Logistic Regression既可以做回归，也可以做分类（二分类为主）。

2. Comparison of Linear Regression, Logistic Classification and Logistic Regression

将logisitic回归与之前学习的二元分类和线性回归做一对比，如图二所示。

图二 Comparison of Three Linear Models ^[2]

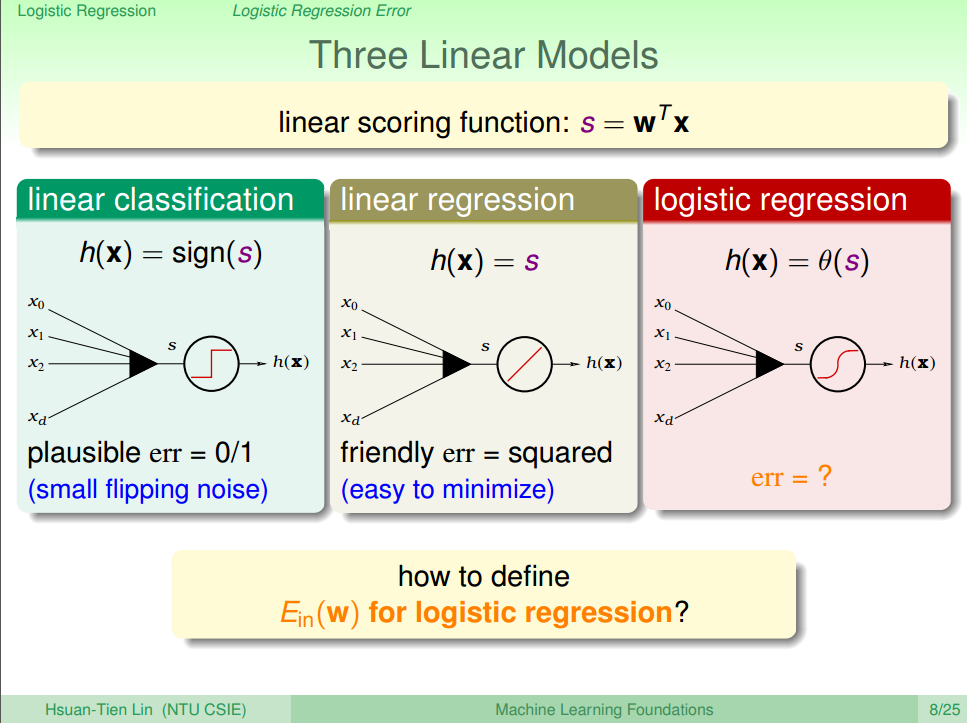
其中分数s是在每个假设函数中都会出现的，前两个学习模型的错误衡量分别对应着0/1错误和平方错误，而logistic回归所使用的err函数应如何表示则是本节要介绍的内容。

3. Error Measurement of Logistic Regression - cross-entropy error

这一节的推导需要对最大似然法和条件概率求解有一定的了解。

TODO:最大似然法 和 条件概率

1.首先从 Logistic Function 可以推导出下面的公式（6），花括号上半部分不难理解，是将目标函数等式左右对调的结果，而下半部分的推导也很简单，因为+1与-1的总概率为1。

f(x)=P(+1|x)⇔P(y|x)={f(x)1−f(x)fory=+1fory=−1(6)

2.假设存在一个数据集 D=(x1,∘),(x2,×),⋯,(xn,×),则通过目标函数产生此种数据集样本的概率可以用公式（7）表示。

P(D)=P{x1}P{∘|x1}×P{x2}P{×|x2}×⋯×P{xn}P{×|xn}(7)

3.把公式（6）的公式带入公式（7)中，可以得到公式（8）。

P(D)=P{x1}f(x1)×P{x2}(1−f(x2))×⋯×P{xn}(1−f(xn))(7)

4.f(x)是理想的函数，而我们实际训练得到的是hypothesis h(x)，所以我们还得想办法用h(x)代替f(x)，但是这样的前提是我们假设函数h(x)对数据集与f(x)产生的可能性很大，即likelihood(似然)，即我们在之前在VC Bound的推论中，知道在数据量足够大的情况下g(x)是会接近于f(x)的，如公式（8）所示

P(D)=P{x1}h(x1)×P{x2}(1−h(x2))×⋯×P{xn}(1−h(xn))(8)

5.那么最大似然我们表示为 likelihood(h)，在代入simoid函数的特性 1−h(x)=h(−x)，可以得到公式（9）

likelihood(h)=P{x1}h(x1)×P{x2}(h(−x2))×⋯×P{xn}(h(−xn))(9)

6.那么最大的likelihood(h)如公式（10）所示，在计算最大的likelihood(h)时，所有P(xi)的对大小没有影响，因为所有的假设函数都会乘以同样的P(xi)，所以在表示的时候可以只考虑h(x)。

maxhlikelihood(logistich)maxwlikelihood(w)maxwlikelihood(w)∝P{x1}h(x1)×P{x2}(h(−x2))×⋯×P{xn}(h(−xn))∝∏i=1nh(yixi)∝∏i=1nh(yiwTxi)∝maxln∏i=1nh(yiwTxi)(10)

7.连乘公式不容易求解最大问题，因此求其对数，此处以自然对数e为底，并代入sigmoid 方程，令err(w,yi,xi)=ln(1+exp(−ywTx))，如公式（11）所示，误差方程 Ein 如公式（12)所示。

maxwlikelihood(w)∝maxln∏i=1nh(yiwTxi)∝minw1N∑i=1n−lnθ(yiwTxi)∝minw1N∑i=1nerr(w,yi,xi)Ein(w)(11)

Ein(w)=1N∑i=1nln(1+exp(−ywTx))(12)

4. Gradient of Logistic Regression Error

上一节中，推导出logistic回归的 ，下一步的工作是寻找使得最小的权值向量w。
对公式（12）进行求导，可以得到公式（13），推导过程参考老师用的方法：用圈圈代替exp里面的数，用正方形代替ln里面的表达式，这样可以使得推导过程看起来更加明白

Ein(w)∂Ein(w)∂wi=1N∑i=1nln(1+exp(−ywTx)◯)□=1N∑i=1n(∂ln(□)∂□)(∂(1+exp(◯))∂◯)(∂−yiwTxi∂wi)=1N∑i=1n(1□)(exp(◯))(−yixi)=1N∑i=1n(exp(◯))(−yixi)∵(1□)≈1=1N∑i=1n(θ(◯))(−yixi)=1N∑i=1n(θ(−yiwTxn))(−yixi)(13)

从公式（13）可以看出，该函数是一个 θ 函数作为权值，关于 (−ynxn) 的加权求和函数。如果函数的所有权值为零，，可以看出 yi与所有的对应的 wTxn 的同号，即线性可分。

但是，求该问题的解不能使用类似求解线性回归时使用的闭式解的求解方式，此最小值又该如何计算？我们可以借鉴之前PLA的方法进行迭代求解，如公式（14）

wt+1=wt+[[sign(wTtxi)≠yi]]yixi(14)

从公式（14）可以看出，当 sign(wTtxi)=yn 的时候，向量不改变，当 sign(wTtxi)≠yn 的时候 要加上 yixi，然后我们把公式（14)做一定的调整得到公式（15），其中多乘以一个1作为更新的步长，用 η表示，PLA中更新的部分用 ν 来代表，表示更新的方向。该算法被称为迭代优化方法（iterative optimization approach）

wt+1=wt+1η⋅[[sign(wTtxi)≠yi]]yixiν=wt+η⋅ν(15)

5. Use Gradient Descent to Minimize the Error of Logistic Regression

上面我们根据PLA的方法求得针对Logistic回归问题的误差方程，现在我们就需要找到最佳的参数 η 和 ν。首先误差方程的曲线图如图三所示。E−in 是关于权值向量 w 的示意图为一个平滑且可微的凸函数，其中图像谷底的点对应着最佳 w。

图三 Iterative Optimization ^[3]

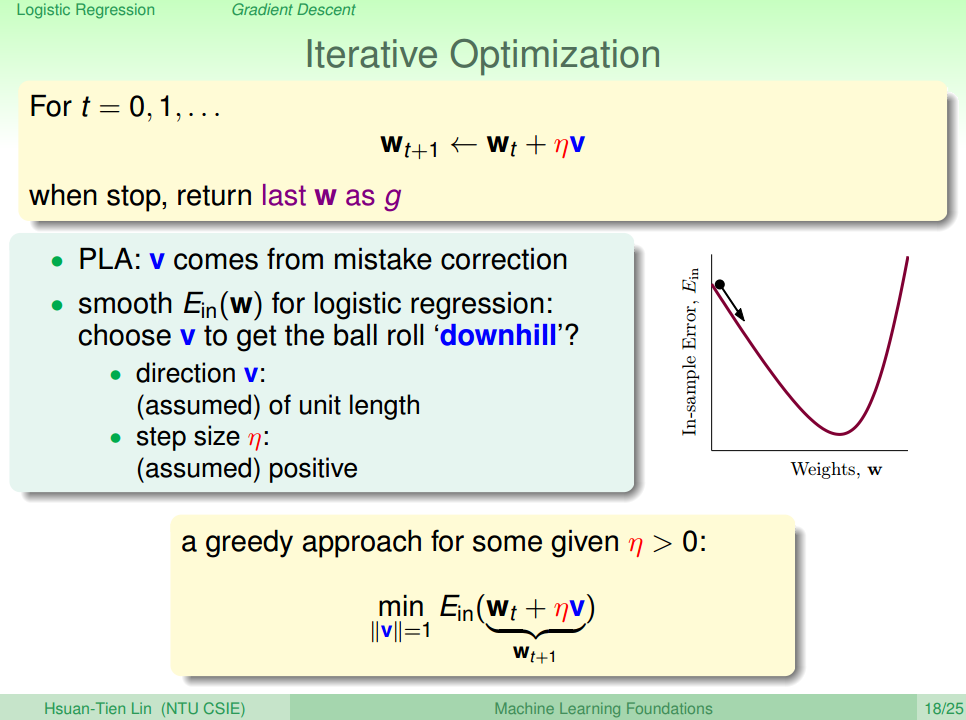
为了分工明确，设 ν 作为单位向量仅代表方向， η 代表步长表示每次更新改变的大小。在 η 固定的情况下，ν 按照最陡峭的方向更改。即在 η 固定 |ν|=1 的情况下，有最快的速度找出使得 Ein 最小的 w，得到公式（16）

min|ν|=1Ein(wi+ην)wt+1(16)

但是公式（16）依然很难求得最小的 w，当 η 很小时，我们通过泰勒展开公式（17）可以得到公式（18），其中 wt 对应 x0

Tylor Expansion

f(x)=f(x0)+f′(x0)1!(x−x0)+f(2)(x0)2!(x−x0)2+⋯+f(n)(x0)n!(x−x0)n+Rn(x)(17)

min|ν|=1Ein(wi+ηνT)≈Ein(wt)+((wt+ηνT)−wt)∇Ein(wt)1!=Ein(wt)+ηνT∇Ein(wt)(18)

接着我们继续分析公式（18），其中 Einwt 我们是知道的， η 是给定的步长， ∇Ein(wt) 也是知道的，所以求解公式（18）的最小值问题，可以转换成求解 νTnablaEin(wt) 的最小值，即公式（19）

min|ν|=1νT∇Ein(wt)(19)

两个向量最小的情况为其方向相反，即内积为负，得到公式（20）,这种情况下 ν 是一个单位向量

min|ν|=1νT∇Ein(wt)ν=−1=−∇Ein(wt)||∇Ein(wt)||(20)

所以把公式（20）带入公式（15），可以得到公式（21）

wt+1=wt−η⋅∇Ein(wt)||∇Ein(wt)||(21)

从公式（21）可以看出，每次更新权值，w都是减少一点（具体多少要看我们谁的哪个的步长，已经误差大小），按照此种方式更新可以找到使得最小的w。此种方式称作梯度下降（gradient descent）。

6. Choose Step Length for Gradient Descent

由上面的公式（21）可以看出，w受 步长大小 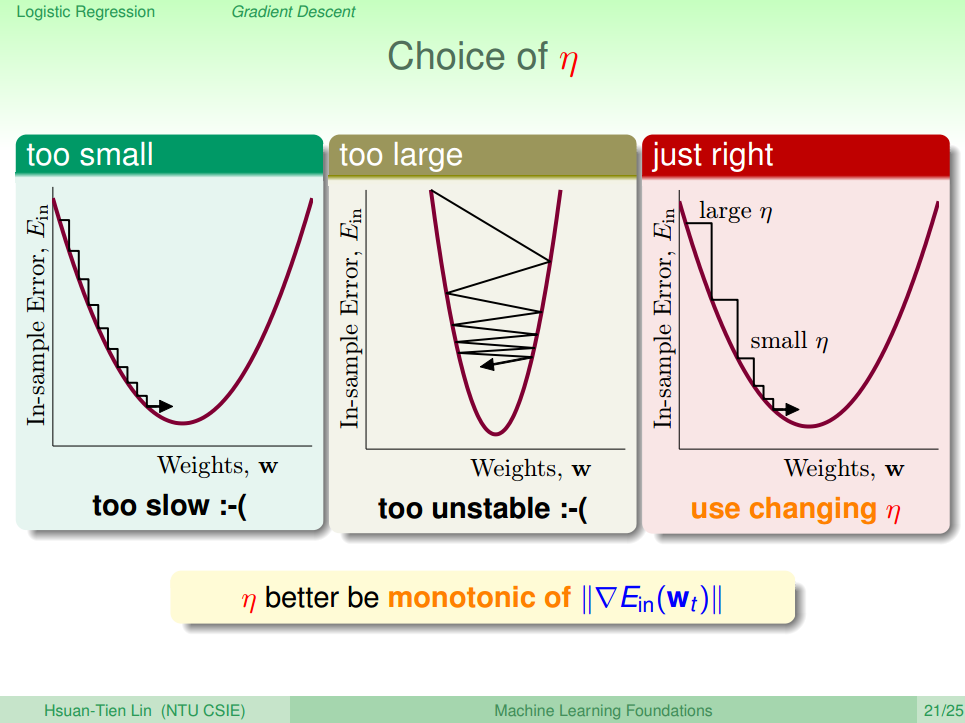η 和 误差大小的影响。在一定的 η 下，越接近谷底，纠正的也越来越小；但是如果选择的 η 太大，一个新就更新到对面的山峰上面去了（可能会导致纠正后误差更大），或者 η 太小，更新好久还没有更新到需要的准确度。所以选择适当的 η 很重要。如图四所示。

图四 Choice of Step Length ^[3]

因为 η 与 梯度大小 ||∇Ein(wt)|| 正比，所以我们可以得到公式（22）

ηnew=ηold||∇Ein(wt)||(22)

结合公式（21）（22），我们调整的公式（21）为（23）

wt+1=wt−ηnew⋅∇Ein(wt)(21)

此时的 η 被称作固定的学习速率（fixed learning rate）。最终得到Logstic Regression 的步骤如下：
1. 设置权值w为 w0，迭代次数他，并计算梯度 ∇Ein(wt)=1N∑i=1nθ(−yiwTtxi)(−yixi)
2. 不断迭代，并更新权值向量w，wt+1=wt−ηnew⋅∇Ein(wt)，直到误差函数的导数近似于0，或者迭代一定的次数。

Gradient Descent 劣势分析：
1. 不稳定:如果选择的步长太大太小，都会对算法有影响
2. 局部最优：如果函数不是凸函数的话，可能存在多个局部最优点，那样的话，Gradient Descent只能找到最近的局部最优。
3. 计算复杂度大，为O(N)，因为导数需要对所有的点进行一次遍历

7. Stochastic Gradient Descent - Another Approach of Gradient Descent

上面讨论了 Gradient Descent,以及计算复杂度大的问题，这一节我们讨论另一种方法，可以将计算复杂度降成O(1)级别。这种方法就是Stochastic Gradient Descent（随机梯度），用符号 ∇werr(w,wi,yi) 表示， 核心思想是：通过N个样本中随机抽取一个样本点求出的梯度取代原来的期望梯度。 随机梯度值可以看做真实的梯度值加上一个噪音，使用随机梯度取代真实梯度做梯度下降的算法称作随机梯度下降 stochastic gradient descent(SGD)。在迭代次数足够多的情况下，平均的随机梯度和平均的真实梯度相差不大。真实梯度与随机梯度的关系如公式（22）所示

∇wEin(wt)=εi⋅∇werr(w,xi,yi)(22)

Logistic Regression 的SGD的迭代如公式(23)所示。

wt+1=wt−η⋅(∇werr(w,xi,yi))(yixi)=wt+ηθ(−yiwTtxi)(yixi)−∇werr(w,xi,yi)(yixi)(23)

对比之前的PLA算法的公式（如公式（24）），容易发现两个公式很类似，因此logistic Regession 的SGD算法又叫”软”PLA，因为权值并没有那么绝对不是1就是0，而是一个在0~1之间的值。如果 η=1 且 wTtxi≈∞ 始终是一个很大的值，则logistic Regession 的SGD相当于是PLA算法。

wt+1=wt+1η[[sign(wtTxi)≠yi]]ν(yixi)(24)

SGD算法关键是找出两个最佳的参数: 迭代次数 t 和学习步长 η。
1. 对于迭代次数 t 只能假设足够步数后是已经做到足够好，即通常设置一个大的数值即可；
2. 学习步长 η通常也很难选定(老师推荐：0.1126)。

SGD算法的优缺点：
1. 优点：计算简单快速，适用于大数据或者流式数据；
2. 缺点：不稳定，需要一定的调试时间。

Summary

1. 首先引入了 Logistic Regression
2. 然后对比了 Logistic Regression 和 Linear Regression, Linear Classification。
3. 接着分析Logistic Regression 的误差方程，梯度方程，并用Gradient Descent 来最小化误差，并分析如何选择步长。

Reference

[1] 机器学习基石(台湾大学-林轩田)\10\10 - 1 - Logistic Regression Problem (14-33)

[2] 机器学习基石(台湾大学-林轩田)\10\10 - 2 - Logistic Regression Error (15-58)

[3] 机器学习基石(台湾大学-林轩田)\10\10 - 4 - Gradient Descent (19-18)