算法复习之------树状数组

早就想着把以前搞acm的算法复习一遍，那可是瑰宝啊，一直没时间，之前面实习就有此感慨，以前学的算法都忘了，明日要去面个不知名的公司，准备下吧，先把树状数组和TRIE图复习下，明天凑合应对。

 

不多说，上问题：

给你一个数组a[N]，假设存int数，对这个数组的操作有2种：(1)修改数组中某元素的值(2)查询该数组任意区间的和。见poj2481.

 

最朴素想法：在原数组上操作，对于每个操作(1)，修改该位置的值，对于(2)操作，遍历数组求和,复杂度为M+Q*N(M为修改次数，Q为查询次数，N为数组size),当N很大时无法忍受。

 

树状数组解决此问题的复杂度为：(M+Q)*log2(N);

 

原理：查询某区间[a,b]的和等价于求解sum(b)-sum(a-1)(sum(k)为[1,k]的和)；故转化为求解前k项和的问题了。联想线段树分段处理的思想，此处不是二分，而是另一种分段方法。其实可用线段树解决之，但没有树状数组处理简单。开另一数组C[N],元素C[k]存储的值为区间[k-lowbit(k]+1,k]的和。lowbit(k)=k表示成二进制后最右边的位代表的十进制数，即k能整除的最大的(2^x);举个例子：6，表示成2进制为00000110,最右边的位为第2位，故lowbit=2^(2-1)=2,6能整除的2的次方为2。上经典图：

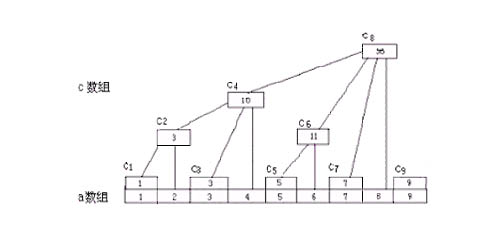
C数组构成一个树状关系：C[x]分布在 log2(lowbit(x)) 层；每个C[k]只有一个父亲节点，子节点与其父节点之间的距离为lowbit(k)。

对于操作(1),修改某位置k的值，则对于数组C要修改包括a[k]的位置，k与下一个相关节点的距离为lowbit(k)。

对于操作(2),查询某位置k的sum(k),则一次查询包括k到1的sum的位置，k与其下一个相关节点的距离为lowbit(k)。

由图可知修改和查询的复杂度都为log2(N);

 

求lowbit很巧妙：x&(x^(x-1));

x:(k1个0或1)1(k2个0)

x-1:(k1个0或1)0(k2个1)

x^(x-1):     (k1个0)1(k2个1)

x&(x^(x-1))     (k1个0)1(k2个0)//即得lowbit(x);

 

看了下另外一个自己写的源码：原来还有一种更简单的lowbit求法：lowbit = x&(-x);

 

x:(k1个0或1)1(k2个0)

~x:(k1个1或0)0(k2个0)

-x=~x+1:        (k1个1或0)1(k2个0)

x&(-x)          (k1个0)1(k2个0)//即得lowbit(x);

 

 

类似巧妙的还有：判断一个数是否为2的次方if((x&-x)==x);

 

代码如下：

int lowbit(int x)//位运算求lowbit(x){return x&(x^(x-1));}void add(int x，int val)//修改位置x的值，val为变化值，可为+-；{while(x <= Max){c[x] += val;x += lowbit(x);}}int getsum(int x)//求sum(x){int result = 0;while(x > 0){result += c[x];x -= lowbit(x);}return result;}

可升级为2维及多维：

修改2维矩阵某个值，求区间[x1,y1]~[x2,y2]的和。类似，代码如下：

int lowbit(int x){return x&(-x);}void add(int x,int y,int det){int i,j;for(i=x;i<=n;i+=lowbit(i))for(j=y;j<=n;j+=lowbit(j))c[i][j]+=det;}int getsum(int x,int y){int i,j,sum=0;for(i=x;i>0;i-=lowbit(i))for(j=y;j>0;j-=lowbit(j))sum+=c[i][j];return sum;}