《Thinking In Algorithm》11.堆结构之二叉堆

堆的变体：

• 二叉堆

• 二项堆

• 斐波那契堆

之前有篇博客（操作系统中堆和栈的区别）讲的是操作系统中的堆，顺带提了下数据结构中的堆。觉得比较简单就没详细讲解，不过这几天看排序算法看到堆排序时，感觉对堆都不怎么熟悉，有些细节问题没注意到。所以说不要小看任何一个知识点。而且经过细看才发现堆其实有很多精妙之处，怪不得很多算法都靠它来实现，如堆排序，Dijkstra算法。

而且堆有许多变体，如二叉堆，二项堆，斐波那契堆。这些我在之后的博客中会一次讲到。

首先我们来简单介绍下最原始的堆。

堆的定义：a heap is a specialized tree-based data structure that satisfies the heap property: If A is a parent node of B then the key of node A is ordered with respect to the key of node B with the same ordering applying across the heap. 

1. 什么是二叉堆？

----------------------------------------------------

一句话概括：二叉堆就是一种满足堆的两个特性的一颗完全二叉树。也叫优先队列

那么是满足哪两个呢？

1. 树是一颗完全二叉树。（除了最后一层可能不饱和，其他都饱和，且最后一层节点是从左往右排满）
2. 父节点要小于等于或者大于等于子节点（根据堆的定义来确定是大于等于还是小于等于）

父节点比子节点大的称为最大堆：

Example of a complete binary max heap

父节点比子节点小的为最小堆：

Example of a complete binary min heap

2. 二叉堆操作

----------------------------------------------------

下面是各种操作的时间复杂度和空间（树的高度为O(logN),基本操作与树的高度成正比）

Binary HeapTypeTreeTime complexity
in big O notation AverageWorst caseSpaceO(n)O(n)SearchNot supportedNot supportedInsertO(1)O(log n)DeleteO(log n)O(log n)

2.1 插入操作

算法流程：

1. 添加元素到树的最底层。
2. 比较插入元素与其父节点的大小关系是否正确，如果正确，则完成。
3. 如果不正确，则该元素与父节点交换位置，然后回到上一步。

向A中插入元素t的代码：

void Insert(int A[], int n, int t) {n++;A[n] = t;int p = n;while(p >1 && A[PARENT(p)] < t){A[p] = A[PARENT(p)];p = PARENT(p);}A[p] = t;return max;}

2.2 删除操作

删除树根节点（最小堆得到最小数，最大堆得到最大数）

算法流程：

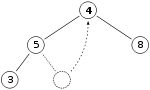
1. 用最后一个元素填补删除的树根
2. 新树根与他的两个孩子作比较；如果顺序正确，则完成。
3. 不正确，则用孩子中的一个交换该元素，回到上一步。（最小堆中选择更小的孩子，最大堆中选择更大的数）

                          ----->----->

实现的伪代码：

void GetMaximum(int A[], int n){int max = A[1];A[1] = A[n];n--;Max-Heapify(A, n, 1);return max;}

上面用到的Max-Heapify操作及修复最大堆的性质。

下面是修复最大堆性质的伪代码：（即对变化后的数组A进行调整使其维持最大堆性质）此处的i是从1开始，不同于编程语言中的数组的索引。i即删除元素所在的位置。

Max-Heapify  (A, i):
 left ← 2i
 right ← 2i + 1
 largest ← i
 if left ≤ heap_length[A] and A[left] > A[largest] then:
 largest ← left
 if right ≤ heap_length[A] and A[right] > A[largest] then:
 largest ← right
 if largest ≠ i then:
 swap A[i] ↔ A[largest]
 Max-Heapify(A, largest)

2.3 堆的创建

即将数组A转变为堆，这里我们可以借用前面提到的Max-Heapify(A,i)算法，但我们并不需要对每一个元素都这行Max-Heapify操作，只需要找到最后一个非叶子节点（即第n/2个元素）以及之前的数进行调整。

BUILD-MAX-HEAP(A)1  heap-size[A] ← length[A]2  for i ← ⌊length[A]/2⌋ downto 13       do MAX-HEAPIFY(A, i)

3. 二叉堆的实现

---------------------------------------------

堆常常用数组来实现，任何一棵二叉树度可以用数组存，但因为二叉堆是一棵完全二叉树，所以他可以紧密的存储，不需要指针来实现。相反，他的孩子节点和父节点可以用数学式来得到，如下：

对于根节点索引为0的树，i节点的孩子节点分别为2i+1和2i+2，父节点为(i-1)/2

A small complete binary tree stored in an array

Comparison between a binary heap and an array implementation.

题目：输入n个整数，输出其中最小的k个。

例如输入1，2，3，4，5，6，7和8这8个数字，则最小的4个数字为1，2，3和4。

分析：这道题之前我有写过一篇关于这道题的博客（查找最小的k个元素），当时我是用的红黑树的数据结构来解决这道题的，我们都知道找出最小的k个数，我们首先利用一个容器来存储k个元素，然后遍历所有数，如果k个元素中最大数大于此时遍历的数，那么只需要替换掉最大数。当时利用红黑树来存储k个元素.同时我们如果利用最大堆的方法，也同样可以达到这样的效果。我们知道红黑树的操作与其树的高度成正比即O(logk)，同样最大堆的操作也与树的高度成正比。所以两者时间复杂度是一样的。