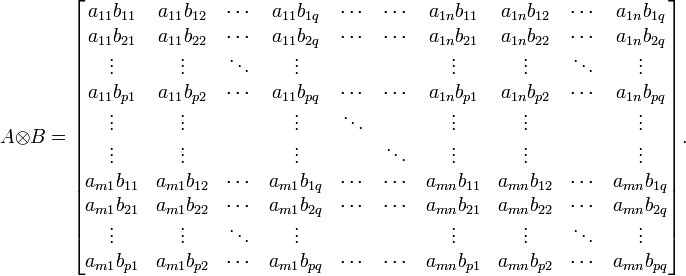克罗内克积
来源:互联网 发布:w7计算机mac地址怎么查 编辑:程序博客网 时间:2024/06/05 06:27
定义[编辑]
如果A是一个 m × n 的矩阵,而B是一个 p × q 的矩阵,克罗内克积 则是一个 mp × nq 的分块矩阵
则是一个 mp × nq 的分块矩阵
更具体地可表示为
例子[编辑]
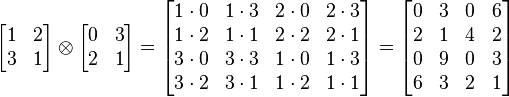 .
.
 .
.
0 0
- 克罗内克积
- 克罗内克积
- 克罗内克积
- 哈达马积&克罗内克积
- 克罗内克积 Kronecker product
- 辨析matmul product(一般矩阵乘积),hadamard product(哈达玛积)、kronecker product(克罗内克积)
- Openfire中调试控制台代码JSP的方法
- 关于使用java从http接口取数据保存到本地文件的中文乱码处理
- RailsCasts32 Time in Text Field 时间类型的输入域
- 关于TextBox.Locked属性
- tomcat6 NIO源码剖析二(NIO工作流程)
- 克罗内克积
- 计算几何-经典算法-凸包
- 你跳槽怎样考虑可持续性发展
- Android精美登录界面设计
- 程序员篇----你是如何减压的?
- mysql 实现row_number() over(partition by ) 分组排序功能
- 使用python构建基于hadoop的mapreduce日志分析平台
- nyoj597完数
- Android分辨率自适应