组合c(m,n)的计算方法

来源：互联网发布：wampserver 配置域名编辑：程序博客网时间：2024/05/31 19:28

问题：求解组合数C(n,m)，即从n个相同物品中取出m个的方案数，由于结果可能非常大，对结果模10007即可。

方案1:

暴力求解，C(n,m)=n*(n-1)*...*(n-m+1)/m!，n<=15

这种方案的缺陷是，在计算过程中很快ans就溢出了，一般情况下，n不能超过12。补救办法之一是将先乘后除改为交叉地进行乘除，先除能整除的，但也只能满足n稍微增大的情况，n最多只能满足两位数。补救办法之二是换用高精度运算，这样结果不会有问题，只是需要实现大数相乘、相除和取模等运算，实现起来比较麻烦，时间复杂度为O(n)。

int Combination(int n, int m) {     const int M = 10007;     int ans = 1;     for(int i=n; i>=(n-m+1); --i)         ans *= i;     while(m)         ans /= m--;     return ans % M; }

方案2:

打表，C(n,m)=C(n-1,m-1)+C(n-1,m)，n<=10,000

由于组合数满足以上性质，可以预先生成所有用到的组合数，使用时，直接查找即可。生成的复杂度为O(n^2)，查询复杂度为O(1)。较方案一而言，支持的数量级大有提升，在1秒内，基本能处理10000以内的组合数。算法的预处理时间较长，另外空间花费较大，都是平方级的，优点是实现简单，查询时间快。

[cpp] const int M = 10007; const int MAXN = 1000; int C[MAXN+1][MAXN+1]; void Initial() {     int i,j;     for(i=0; i<=MAXN; ++i)     {         C[0][i] = 0;         C[i][0] = 1;     }     for(i=1; i<=MAXN; ++i)     {         for(j=1; j<=MAXN; ++j)         C[i][j] = (C[i-1][j] + C[i-1][j-1]) % M;     } } int Combination(int n, int m) {     return C[n][m]; }

方案3:

质因数分解，C(n,m)=n!/(m!*(n-m)!)，设n!分解因式后，质因数p的次数为a；对应地m!分解后p的次数为b；(n-m)!分解后p的次数为c；则C(n,m)分解后，p的次数为a-b-c。计算出所有质因子的次数，它们的积即为答案，即C(n,m)=p1 ^a1-b1-c1p2 ^a2-b2-c2…pk ^ak-bk-ck。n!分解后p的次数为：n/p+n/p ²+…+n/p ^k。

算法的时间复杂度比前两种方案都低，基本上跟n以内的素数个数呈线性关系，而素数个数通常比n都小几个数量级，例如100万以内的素数不到8万个。用筛法生成素数的时间接近线性。该方案1秒钟能计算 1kw数量级的组合数。如果要计算更大，内存和时间消耗都比较大。

#include <cstdio>  const int maxn=1000000; #include <vector>  using namespace std; bool arr[maxn+1]={false}; vector<int> produce_prim_number() {         vector<int> prim;         prim.push_back(2);         int i,j;         for(i=3;i*i<=maxn;i+=2)         {                 if(!arr[i])                 {                         prim.push_back(i);                         for(j=i*i;j<=maxn;j+=i)                                 arr[j]=true;                 }         }         while(i<maxn)         {                 if(!arr[i])                         prim.push_back(i);                 i+=2;         }         return prim; } //计算n!中素数因子p的指数  int cal(int x,int p) {         int ans=0;         long long rec=p;         while(x>=rec)         {                 ans+=x/rec;                 rec*=p;         }         return ans; } //计算n的k次方对m取模，二分法  int pow(long long n,int k,int M) {         long long ans=1;         while(k)         {                 if(k&1)                 {                         ans=(ans*n)%M;                 }                 n=(n*n)%M;                 k>>=1;         }         return ans; } //计算C（n，m）  int combination(int n,int m) {         const int M=10007;         vector<int> prim=produce_prim_number();         long long ans=1;         int num;         for(int i=0;i<prim.size()&&prim[i]<=n;++i)         {                 num=cal(n,prim[i])-cal(m,prim[i])-cal(n-m,prim[i]);                 ans=(ans*pow(prim[i],num,M))%M;         }         return ans; } int main() {         int m,n;         while(~scanf("%d%d",&m,&n),m&&n)         {                 printf("%d\n",combination(m,n));         }         return 0; }

方案四

Lucas定理，设p是一个素数（题目中要求取模的数也是素数），将n,m均转化为p进制数，表示如下：

满足下式：

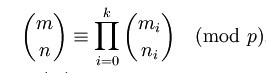
即C(n,m)模p等于p进制数上各位的C(ni,mi)模p的乘积。利用该定理，可以将计算较大的C(n,m)转化成计算各个较小的C(ni,mi)。

该方案能支持整型范围内所有数的组合数计算，甚至支持64位整数，注意中途溢出处理。该算法的时间复杂度跟n几乎不相关了，可以认为算法复杂度在常数和对数之间。

#include <stdio.h>const int M = 10007;int ff[M+5];  //打表，记录n!，避免重复计算//求最大公因数int gcd(int a,int b){    if(b==0) return a; else return gcd(b,a%b);}//解线性同余方程，扩展欧几里德定理int x,y;void Extended_gcd(int a,int b){    if(b==0)    {       x=1;       y=0;    }    else    {       Extended_gcd(b,a%b);       long t=x;       x=y;       y=t-(a/b)*y;    }}//计算不大的C(n,m)int C(int a,int b){    if(b>a) return 0;    b=(ff[a-b]*ff[b])%M;    a=ff[a];    int c=gcd(a,b);    a/=c;    b/=c;    Extended_gcd(b,M);    x=(x+M)%M;    x=(x*a)%M;    return x;}//Lucas定理int Combination(int n, int m){        int ans=1; int a,b; while(m||n) {         a=n%M; b=m%M; n/=M; m/=M; ans=(ans*C(a,b))%M; } return ans;}int main(void){        int i,m,n; ff[0]=1; for(i=1;i<=M;i++)  //预计算n! ff[i]=(ff[i-1]*i)%M;  scanf("%d%d",&n, &m); printf("%d\n",func(n,m));  return 0;}

0 0