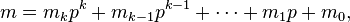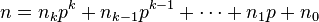Lucas定理 大组合数取模
来源:互联网 发布:linux监控进程脚本 编辑:程序博客网 时间:2024/05/28 11:28
转自AC_Von
http://www.cnblogs.com/vongang/archive/2012/12/02/2798138.html
组合数取模 Lucas定理
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。
这里用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
代码:
typedef long long LL;using namespace std;LL exp_mod(LL a, LL b, LL p) { LL res = 1; while(b != 0) { if(b&1) res = (res * a) % p; a = (a*a) % p; b >>= 1; } return res;}LL Comb(LL a, LL b, LL p) { if(a < b) return 0; if(a == b) return 1; if(b > a - b) b = a - b; LL ans = 1, ca = 1, cb = 1; for(LL i = 0; i < b; ++i) { ca = (ca * (a - i))%p; cb = (cb * (b - i))%p; } ans = (ca*exp_mod(cb, p - 2, p)) % p; return ans;}LL Lucas(int n, int m, int p) { LL ans = 1; while(n&&m&&ans) { ans = (ans*Comb(n%p, m%p, p)) % p; n /= p; m /= p; } return ans;}int main() { Read(); int n, m, p; while(~scanf("%d%d%d", &n, &m, &p)) { printf("%lld\n", Lucas(n, m, p)); } return 0;}
0 0
- Lucas定理 大组合数取模
- 费马小定理+Lucas定理 大组合数取模
- hdu3037 大组合数取模(Lucas定理)
- Lucas定理--大组合数取模 学习笔记
- HDU3944 DP?(大组合数取模:lucas定理)
- Lucas定理(大组合数取模)
- 大组合数取模 Lucas定理 HD3037
- HDU3037(Lucas定理求大组合数取模)
- 【 Lucas定理 】 组合数取模
- Lucas定理---组合数取模
- lucas 定理,组合数取模
- FZU 2020 组合 -- (大组合数取模 Lucas定理)
- hdu 3037 Saving Beans 【大组合数取模-Lucas定理+逆元取模】
- 大组合数取模 hdu 3037 Saving Beans lucas定理
- hdu 3944 Lucas定理--大组合数取模 多校赛
- hdu-3037(lucas定理求大组合数取模)
- hdu 3037(Lucas定理,大组合数取模)
- Lucas定理应用分析——大组合数取模
- 将pdf转换成html的方法
- lambda表达式&委托
- leetcode 112 —— Path Sum
- SIP协议详解&eXosip源码库用法分析
- 依赖权重的随机选择
- Lucas定理 大组合数取模
- android 调用系统相机拍照返回Intent 为空的处理
- 编译zlib遇到的问题 没有找到match686.obj
- linux ssh授权 无密码登录
- cron表达式
- centos7 设置IP/开机启动
- Num 26 : HDOJ2187 : 悼念512汶川大地震遇难同胞——老人是真饿了 [ 贪心 ]
- Linux | 管道
- POJ 2991 Crane (线段树)