Codeforces Round #315 (Div. 1) B. Symmetric and Transitive(Bell数的应用)(好题)
来源:互联网 发布:美国读博士条件知乎 编辑:程序博客网 时间:2024/05/29 18:29
大致题意:
A set ρ of pairs (a, b) of elements of some set A is called a binary relation on set A. For two elements a and b of the set A we say that they are in relation ρ, if pair 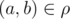 , in this case we use a notation
, in this case we use a notation  .
.
Binary relation is equivalence relation, if:
- It is reflexive (for any a it is true that
 );(自反律)
);(自反律) - It is symmetric (for any a, b it is true that if
 , then
, then 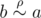 ); (交换律)
); (交换律) - It is transitive (if
 and
and 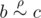 , than
, than  ).(传递律)
).(传递律)

给出了等值Binary relation的定义,给定数的全集{1,2,3...,n}求有多少个ρ 集合满足等值关系中的2,3两条而不满足第一条
题意真是难理解...
思路:
只要有某个元素a满足了2,3两条,就一定由  和
和 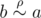 推出
推出 ,所以这个元素就满足了第一条
,所以这个元素就满足了第一条
同理如果这个集合中的每个元素满足2,3条那么每个元素都满足第一条也就是此集合成为了等值Binary relation。
所以为了不成为等值Binary relation,必须至少有一个元素x不满足所有关系,也就是不参与构成了某个二元组,除x外的元素恰好构成了等值Binary relation。
所以本题的答案就是 sigama(i:0,n-1){ C(n,i)*(这i元素构成的等值Binary relation的个数) }
现在问题变成i个元素可以构成多少个等值Binary relation
这个问题可以用递推解决,求dp[i],对于第i个元素必须满足这三个条件才行,所以必须让第i个元素与i-1个元素中的k个元素“混合”才行
比如{(a~b),(b~a),(a~a)}混入c后要满足等值Binary relation则变成{(a~b),(b~a),(b~c),(c~b),(a~c),(c~a),(a~a),(b~b),(c~c)}只有唯一的混合结果
所以dp[i] = sigma(k:0,i-1){ C(i-1,k)*dp[i-1-k] } = sigma(k:0,i-1){ C(i-1,i-1-k)*dp[i-1-k] } = sigma(k:0,i-1){ C(i-1,k)*dp[k] }
会发现这就是Bell数的递推公式
所以求“i个元素可以构成多少个等值Binary relation”这个问题等价与“i的集合的划分方法的数目",例如:
集合{a, b, c}有5种不同的划分方法:
- {{a}, {b}, {c}}
- {{a}, {b, c}}
- {{b}, {a, c}}
- {{c}, {a, b}}
- {{a, b, c}};
每个块中都是前面所说的混合构造成等值Binary relation,所以知道bell数的会很容易解决此问题,到此问题已经圆满解决
//#pragma comment(linker, "/STACK:1024000000,1024000000")#include <iostream>#include <cstring>#include <cmath>#include <queue>#include <stack>#include <map>#include <set>#include <string>#include <vector>#include <cstdio>#include <ctime>#include <bitset>#include <algorithm>#define SZ(x) ((int)(x).size())#define ALL(v) (v).begin(), (v).end()#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)#define reveach(i, v) for (__typeof((v).rbegin()) i = (v).rbegin(); i != (v).rend(); ++ i)#define REP(i,n) for ( int i=1; i<=int(n); i++ )#define rep(i,n) for ( int i=0; i< int(n); i++ )using namespace std;typedef long long ll;#define X first#define Y secondtypedef pair<int,int> pii;template <class T>inline bool RD(T &ret) { char c; int sgn; if (c = getchar(), c == EOF) return 0; while (c != '-' && (c<'0' || c>'9')) c = getchar(); sgn = (c == '-') ? -1 : 1; ret = (c == '-') ? 0 : (c - '0'); while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0'); ret *= sgn; return 1;}template <class T>inline void PT(T x) { if (x < 0) { putchar('-'); x = -x; } if (x > 9) PT(x / 10); putchar(x % 10 + '0');}const int N = 4000+123;const int MOD = 1e9+7;int bell[N][N];int C[N][N];int main(){ bell[0][0] = 1; REP(i,N-10) REP(j,i){ if(j == 1) bell[i][j] = bell[i-1][i-1]; else bell[i][j] = (bell[i][j-1]+bell[i-1][j-1])%MOD; } REP(i,N-10) { C[i][i] = C[i][0] = 1; REP(j,i-1) C[i][j] = (C[i-1][j-1]+C[i-1][j])%MOD; } int n; while(~scanf("%d",&n)){ ll ans = 0; rep(i,n) ans = (ans+C[n][i]*(ll)bell[i][i])%MOD; PT(ans),puts(""); }}作为弱渣第一次遇过bell数,现在补充记录一些常用的基础知识:
Stirling数,第一类有点难理解不在此记录
第二类Stirling数是 个元素的划分成k个非空集合的方法数目。常用的表示方法有
个元素的划分成k个非空集合的方法数目。常用的表示方法有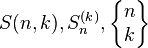 。
。
- 给定
 ,有递归关系
,有递归关系
证明递推式:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合,有 种方法;也可以前n-1种物品构成k个非空的不可辨别的集合,第n个物品放入任意一个中,这样有
种方法;也可以前n-1种物品构成k个非空的不可辨别的集合,第n个物品放入任意一个中,这样有 种方法。
种方法。
Bell数:n的集合的划分方法的数目。
由定义可以得出它和第二类stirling数的关系: ,即划分成k个非空集合
,即划分成k个非空集合
有两个递推关系可以求bell数:
1.
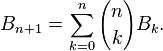
上述组合公式的证明:
可以这样来想,B_{n+1}是含有n+1个元素集合的划分的个数,考虑元素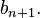
假设他被单独划分到一类,那么还剩下n个元素,这种情况下划分个数为 ;
;
假设他和某一个元素被划分为一类,那么还剩下n-1个元素,这种情况下划分个数为 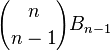 ;
;
假设他和某两个元素被划分为一类,那么还剩下n-2个元素,这种情况下划分个数为  ;
;
依次类推,得到了上述组合公式
2.根据贝尔三角形递推(较方便形象)
用以下方法建构一个三角矩阵(形式类似杨辉三角形):
- 第一行第一项是1(
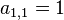 )
) - 对于n>1,第n行第一项等同第n-1行最后一项。(
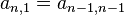 )
) - 对于m,n>1,第n行第m项等于它左边和左上方的两个数之和。(
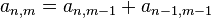 )
)
结果如下:(OEIS:A011971)
每行首项是贝尔数。
摘自:
https://zh.wikipedia.org/wiki/%E8%B4%9D%E5%B0%94%E6%95%B0
https://zh.wikipedia.org/wiki/%E6%96%AF%E7%89%B9%E7%81%B5%E6%95%B0
- Codeforces Round #315 (Div. 1) B. Symmetric and Transitive(Bell数的应用)(好题)
- Codeforces Round #315 (Div. 1) B. Symmetric and Transitive 斯特林数 贝尔数
- [组合数+bell数] codeforces 569D. Symmetric and Transitive
- codeforces 569 D. Symmetric and Transitive (bell数)
- Codeforces Round #315 (Div. 2) D. Symmetric and Transitive
- CodeForces #315 (div1) B.Symmetric and Transitive
- codeforces #315B. Symmetric and Transitive dp
- Codeforces Round #315 (Div. 2)569D Symmetric and Transitive(dp)
- codeforces 568B B. Symmetric and Transitive(贝尔数+组合数学)
- codeforces #568B Symmetric and Transitive 快速傅里叶变换
- Codeforces Round #250 (Div. 1) B. The Child and Zoo(排序+并查集)(常规好题)
- Codeforces Round #419 (Div. 1) B. Karen and Test(组合数)
- LCA好(Codeforces Round #294 (Div. 2)E. A and B and Lecture Rooms)
- Divide by Zero 2017 and Codeforces Round #399 (Div. 1 + Div. 2, combined) B. Code For 1(DFS好题)
- Codeforces Round #329 (Div. 2) B. Anton and Lines ([好题] 计算直线在区间是否有交点)
- CF 568B Symmetric and Transitive 贝尔数和stirlinig数
- Codeforces Round #257 (Div. 1)B题Jzzhu and Cities(spfa+slf优化)
- B. Amr and Pins( Codeforces Round #287 (Div. 2))
- 资料
- 当敏捷开发遇上了千年老怪的老系统....
- readline函数实现源码
- BZOJ 题目1016: [JSOI2008]最小生成树计数(Kruskal+Matrix_Tree)
- jquery 选择器的一些小操作
- Codeforces Round #315 (Div. 1) B. Symmetric and Transitive(Bell数的应用)(好题)
- 【DP】poj2486
- HttpUrlConnection网络连接
- 线程与进程的区别
- ios中的UIAutomation脚本的录制
- Java ImageIcon 不能显示问题
- hdu5354 Bipartite Graph
- Java从键盘输入值
- Android之——JNI与C语言常见术语
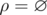 . In other words, for a single element
. In other words, for a single element 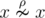 .
.


