线性代数：第一章 行列式（1）n阶行列式 行列式的性质

第一节 n阶行列式

一．数学概念

1． 逆序数

对于n个不同的元素，先规定各元素之间有一个标准次序(例如n个不同的自然数，可规定由小到大为标准次序)，于是在这n个元素的任一排列中，当某两个元素的先后次序与标准次序不同时，就说有1个逆序。一个排列中所有逆序的总数叫做这个排列的逆序数。

2． 奇排列与偶排列

逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列。

3． 对换

在排列中，将任意两个元素对调，其余的元素不动，这种作出新排列的手续叫做对换。将相邻两个元素对换，叫做相邻对换)

4． n阶列式

定义  设有n² 个数，排成n行n列的数表

作出表中位于不同行不同列的n个数的乘积，并冠以符号(-1) ^τ ，得到形如

的项，其中p₁,p₂,…,p_n,为自然数1,2,…,n的一个排列，为这个排列的逆序数。由于这样的排列共有n!个，因而形如上式的项共有n!项。所有这n!的代数和

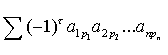
称为n阶行列式，记作

简记作det(  )。数  称为行列式det(  )的元素。

二．基本原理公式

定理1.1  一个排列中的任意两个元素对换，排列改变奇偶性。

推论  奇排列调成标准排列的对换次数为奇数，偶排列调成标准排列的对换次数为偶数。

定理1.2　n阶行列式也可定义为

其中t为行标排列  的逆序数。

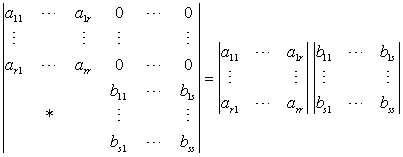
公式1　

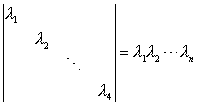
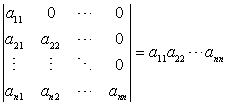
公式2

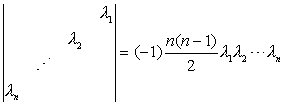
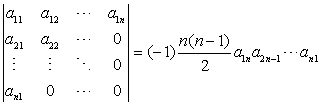
公式3　

三．重点、难点分析

逆序数的概念和n阶行列式的定义都比较抽象，难以理解。但要抓住实质，找出规律，就能透彻理解这些概念的实质。

关于求一个排列  的逆序数，它等于每个数字  的逆序之和，而对于  的逆序，可以求排列中  后面的数中比  小的数的个数，也可以求排列中  前面的数中比  大的数的个数。

关于n阶行列式，它的计算结果是一个数或者是一个多项式，而它的一般项是每一行取一个元素(而且仅仅取一个元素)，要求取在不同的列上的n个元素的乘积。把这n个元素的行标(列标)排成自然排序，其相应列标(或行标)的排列为 。它是1,2,…,n这n个数组成的全排列中的某一个n级排列。该项所带符号即是该列标(行标)排列的逆序数的奇偶性所决定的。对一般项(n!个)求和，即为行列式的值。

易见，若用行列式的定义来计算行列式是十分复杂和困难的。所以，我们用n阶行列式的定义计算出三个特殊的公式。以后可以直接用该公式计算行列式。但是如何把一个一般的行列式化成三个公式的形式，那就是下节要学的重要内容，即行列式的性质。

行列式的定义是行列式计算的基础，是学习行列式的重点。

四．典型例题分析

例1．设

 ，

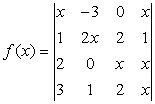则  中  的系数为_______；  的系数为_______；常数项为_______。

解：本解的解法主要是用行列式的定义，因为  是关于未知数是x的一个4次多项式，而含x⁴的项只有一项 ，含  的项有两项  和  ，常数项为  。故  的系数为2，  的系数为－10，常数项为12。

第二节 行列式的性质

一．数学概念

转置行列式

设

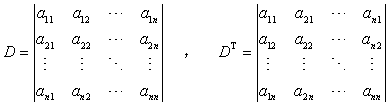
行列式D^T称为行式列D的转置行列式。

二．基本性质

性质1　行列式与它的转置行列式相等。

性质2　互换行列式的两行(列)，行列式变号。

推论　如果行列式有两行(列)完全相同，则此行列式为零。

性质3　行列式的某一行(列)中所有的元素都乘以同一数k，等于用数k乘此行列式。

推论　行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。

性质4　行列式中如果有两行(列)元素成比例，则此行列式等于零。

性质5　若行列式的某一行(列)的元素都是两数之和，例如第j列的元素都是两数之和：

              

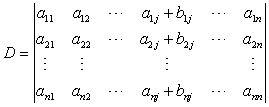
则D等于下列两个行列式之和

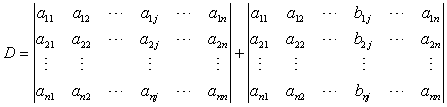
性质6　把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变。

三．重点，难点分析

行列式的六条基本性质是把一般的行列式变成第一节所给出的三个基本公式的钥匙，它是计算行列式必须掌握的重要理论，其难点就是如何灵活运用行列式的六条基本性质，巧妙而简捷地计算出行列式的值，掌握运算的技巧可以提高运算的速度和准确率，从而达到事半功倍的效果。

四．典型例题分析

我们知道，给出行列式的定义后，用定义直接计算行列式是比较麻烦的，例如，计算4阶行列式，用定义去计算要算24项，一个n阶的如行列式要算n!个项的代数和，但只有行列式的六条基本性质之后，就可使运算化简，从而快速计算行列式。

例2．计算

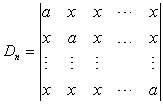
解：由于该行列式的所有列加到一起得同一个数a+(n-1)x，我们就根据这一特点，用行列式的性质6，将D_n的第2列，第3列，…，第n列的1倍同时加到第1列上去，再由性质3的推论，将公因子a+(n-1)x提出来，得

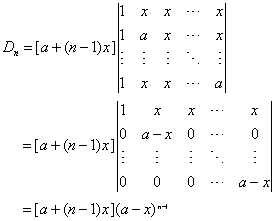
通过上面例题，我们看到主要是行列式的性质将一个行列式化成公式形式，再直接用公式的结果。这虽然比直接用定义计算简单，但是，还要经过许多步的运算才能得出结果。并且，我们在计算中还体会到计算阶数低的行列式要比阶数高的行列式简单，所以我们继续探求新的计算行列式的方法。

from: http://dec3.jlu.edu.cn/webcourse/t000022/teach/index.htm