CF 396A On Number of Decompositions into Multipliers(组合数学)

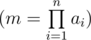You are given an integer m as a product of integersa₁, a₂, ...a_n. Your task is to find the number of distinct decompositions of numberm into the product ofn ordered positive integers.

Decomposition into n products, given in the input, must also be considered in the answer. As the answer can be very large, print it modulo1000000007(10⁹ + 7).

Input

The first line contains positive integer n (1 ≤ n ≤ 500). The second line contains space-separated integersa₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹).

Output

In a single line print a single number k — the number of distinct decompositions of numberm inton ordered multipliers modulo1000000007(10⁹ + 7).

Examples

Input

115

Output

1

Input

31 1 2

Output

3

Input

25 7

Output

4

Note

In the second sample, the get a decomposition of number 2, you need any one number out of three to equal 2, and the rest to equal 1.

In the third sample, the possible ways of decomposing into ordered multipliers are [7,5], [5,7], [1,35], [35,1].

A decomposition of positive integer m inton ordered multipliers is a cortege of positive integersb = {b₁, b₂, ...b_n} such that 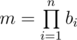. Two decompositionsb and c are considered different, if there exists indexi such that b_i ≠ c_i.

题意：有n个数，把这n个数分为a1到an个数连乘。（比方说n为2,这两个数为3,5，则可以有1,35； 5,7； 7,5；35,1；）

分析：可以将这n个数全部分解为素因子，然后将每种素因子（设为k个）分别放到n个位置。用隔板法求得为每种总数为c（n+m-1，n-1）。

          

#include<cstdio>#include<cstring>#include<iostream>#include<map>#define LL  long long#define N 37000const int  MOD=1e9+7;using namespace std;map<int,int> mp;bool is[N+10];LL prime[N],k,n;LL jc[N+10],fjc[N+10];void addm(int x){    for(int i=1;prime[i]*prime[i]<=x;i++)    {        while(x%prime[i]==0)        {            mp[prime[i]]++;           x/=prime[i];        }        if(x==1)break;    }    if(x>1)mp[x]++;}LL quickmi(LL x,LL m)   //快速幂{    LL ans=1;    while(m>0)    {        if(m&1)            ans=(ans*x)%MOD;        x=x*x%MOD;        m/=2;    }    return ans;}LL CC(int n,int m){   if(m==0)return 1;     //cout<<jc[n]<<" "<<fjc[m]<<endl;    return jc[n]*fjc[m]%MOD*fjc[n-m]%MOD;}int main(){    k=0;    memset(is,true,sizeof(is));    is[0]=is[1]=0;    for(int i=2;i<=N;i++)    {        if(is[i])        {            prime[++k]=i;            for(int j=i*i;j<=N;j+=i)is[j]=false;        }    }    jc[0]=1;    for(int i=1;i<=N;i++)    {        jc[i]=jc[i-1]*i%MOD;        fjc[i]=quickmi(jc[i],MOD-2);  //阶乘的逆模元，费马小定理        //if(i<20)        //cout<<jc[i]<<" "<<fjc[i]<<endl;    }    int x;    while(scanf("%d",&n)!=EOF)    {        mp.clear();        for(int i=1;i<=n;i++)        {            scanf("%d",&x);            addm(x);        }        LL ans=1;        map<int,int>::iterator it;        for(it=mp.begin();it!=mp.end();it++)        {            x=it->second;           //printf("%d\n",x);            ans=ans*CC(n+x-1,n-1)%MOD;        }        printf("%I64d\n",ans);    }    return 0;}