[POJ] 2528

Mayor's posters

Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 70483 Accepted: 20331

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
  
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
  
• The wall is divided into segments and the width of each segment is one byte. 
  
• Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri.

Output

For each input data set print the number of visible posters after all the posters are placed. 

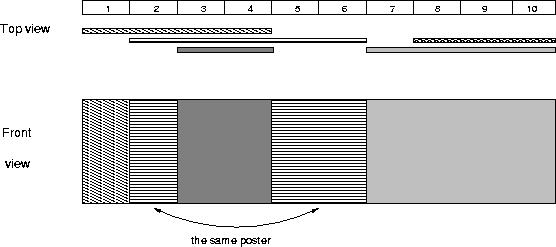
The picture below illustrates the case of the sample input. 

Sample Input

151 42 68 103 47 10

Sample Output

4

Source

Alberta Collegiate Programming Contest 2003.10.18

给你一个个区间

你要贴广告

每次后面的广告会盖上前面的广告

询问最后能看到多少个广告

线段树的题

好像刚开始想歪了

我也不知道怎么想歪的

其实只要到把贴广告的顺序倒过来

这样如果每次贴的广告能覆盖到未被贴广告的区间

那就说明这个广告能被看到

然后用线段树维护

每个节点有左节点右节点的编号

以及左右节点编号包含的区间是否被贴广告（0为未被贴， 1为被贴）

每次贴广告的时候从树顶往下更新

如果扫到一个节点的广告标记为 1

那就不往下扫了

如果区间恰好重叠就把广告标记标记为1

同时每轮贴广告ans只加一次

同时这道题需要离散化

然后离散化还不是一般的离散化

例如

3

1 10

1 3

8 10

答案是 3

离散化以后是

1 4

1 2

3 4

这样答案就成2了，，

所以防止这种情况

第一次离散化以后XJB判一下就好了

刚开始忘记写up操作了WA了

#include <cstdio>#include <cstring>#include <algorithm>#include <iostream>using namespace std;const int N = 400100;struct  Three{int l;int r;int mark;};struct Quary{    int l;    int r;};Quary quary[N];Three tree[N * 4];int n;int mark;int ans;int al[N];int ar[N];void up(int x){    if(tree[x << 1].mark == 1 && tree[x << 1 | 1].mark == 1){        tree[x].mark = 1;    }}void build(int x, int l, int r){tree[x].l = l;tree[x].r = r;tree[x].mark = 0;if(l != r){int mid = l + ((r - l) >> 1);build(x << 1, l, mid);build(x << 1 | 1, mid + 1, r);up(x);}}void update(int x, int l, int r){int ll = tree[x].l;int rr = tree[x].r;if(l > r || tree[x].mark){return ;}if(ll == l && rr == r){if(!mark){mark = 1;ans ++;tree[x].mark = 1;}else{tree[x].mark = 1;}}else{        int mid = ll + ((rr - ll) >> 1);        update(x << 1, l, min(mid, r));        update(x << 1 | 1, max(mid + 1, l), r);        up(x);}}int main(int argc, char const *argv[]){int ncase;scanf("%d", &ncase);while(ncase --){ans = 0;scanf("%d", &n);int rec[N], p = 0;for(int i = 0; i < n; i ++){scanf("%d%d", &quary[i].l, &quary[i].r);rec[p++] = quary[i].l;rec[p++] = quary[i].r;}/*小太阳写的离散化*/        sort(rec, rec + p);        p = unique(rec, rec + p) - rec;        int tmp = p;for(int i = 1; i < tmp; ++i)            if(rec[i] - rec[i-1] > 1)rec[p++] = rec[i-1] + 1;        sort(rec, rec + p);        p = unique(rec, rec + p) - rec;        /*小太阳写的离散化*/        build(1, 1, p);for(int i = n - 1; i >= 0; i --){            int lll = lower_bound(rec, rec + p, quary[i].l) - rec + 1;            int rrr = lower_bound(rec, rec + p, quary[i].r) - rec + 1;            mark = 0;            update(1, lll, rrr);}printf("%d\n", ans);}return 0;}