非常仔细明了 关于如何求解多边形面积

转载地址：http://blog.csdn.net/pizi0475/article/details/6300463

感谢作者！致敬

                                       

                          從醉月湖的面積談起
                              向量微積分簡介 （第 2 頁）

                                      蔡聰

2.多邊形的面積公式

多邊形仍然太複雜，我們再退到三角形的特例，探尋完成後，再進到多邊形。這種處理問題時退、進之道很值得留意。

 

問題3：

已知三角形三個頂點的坐標為 A= (x₁, y₁),B = (x₂, y₂),C = (x₃, y₃), 如何求其面積？

我們進一步退到三個頂點為 O=(0,0), B=(x₂,y₂), C=(x₃,y₃) 之更特殊三角形。令 OB, OC 與x 軸的夾角分別為 與，且,，則

 

 

 

 

---

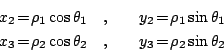
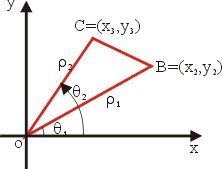
圖3

---

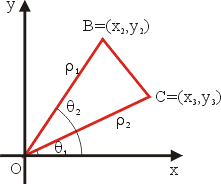
圖4

如上圖所示，我們分成兩種情形來討論：

(i)當 O,B,C 成為逆時針（或右手系）定向時，如圖3，則 的面積為

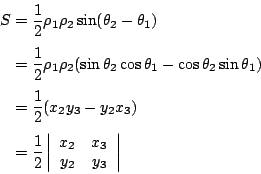(2)

 

(ii)當 O,B,C 成為順時針（或左手系）定向時，如圖4，則 的面積為

 

 

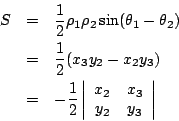
因此行列式

 

 

 

代表由 OB 與 OC 所生成的平行四邊形的有號面積，當O,B,C 逆時針定向時為正，順時針定向時為負。利用向量外積也可以推導出這個結果。

回到問題3，不妨假設 為逆時針走向，見圖5，則 的面積為

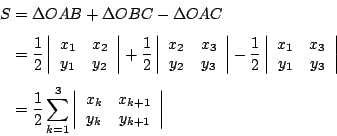(3)

 

其中規定 x₄=x₁ 且y₄=y₁

 

註：

通常教科書將(3)式寫成

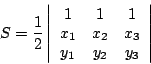(4)

 

不過，(3)式適於推廣到任何多邊形，而(4)式則不然。換言之，(4)式是死的，(3)式才是活的有源之泉。

---

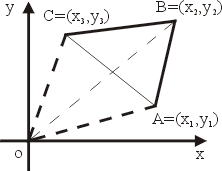
圖5

仿上述之論證可得

定理1：

設 A₁ (x₁ , y₁) ,A₂ (x₂ , y₂) , … ,A_n (x_n,y_n) 為n 邊形之頂點坐標且為逆時針定向，則此 n 邊形的面積為

 

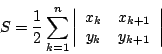(5)

 

其中規定 x_n+1=x₁ 且y_n+1=y₁

 

註：

(5)式又叫做測量師的公式。