图的割点

割点与连通度

在无向连通图中，删除一个顶点v及其相连的边后，原图从一个连通分量变成了两个或多个连通分量，则称顶点v为割点，同时也称关节点(Articulation Point)。一个没有关节点的连通图称为重连通图(biconnected graph)。若在连通图上至少删去k 个顶点才能破坏图的连通性，则称此图的连通度为k。

关节点和重连通图在实际中较多应用。显然，一个表示通信网络的图的连通度越高，其系统越可靠，无论是哪一个站点出现故障或遭到外界破坏，都不影响系统的正常工作；又如，一个航空网若是重连通的，则当某条航线因天气等某种原因关闭时，旅客仍可从别的航线绕道而行；再如，若将大规模的集成电路的关键线路设计成重连通的话，则在某些元件失效的情况下，整个片子的功能不受影响，反之，在战争中，若要摧毁敌方的运输线，仅需破坏其运输网中的关节点即可。

简单的例子

(a)中G7 是连通图，但不是重连通图。图中有三个关节点A、B 和G 。若删去顶点B 以及所有依附顶点B 的边，G7 就被分割成三个连通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。类似地，若删去顶点A 或G 以及所依附于它们的边，则G7 被分割成两个连通分量。

low[u]=  {min{low[u], low[v]}，(u,v)为树边

               min{low[u], dfn[v]}      (u,v)为回边且v不为u的父亲节点

下表给出图(a)对应的dfn与low数组值。

i0123456789101112vertexABCDEFGHIJKLMdfn[i]15121011138694723low[i]1115515582511

求割点的方法

暴力的方法：

• 依次删除每一个节点v
  
• 用DFS（或BFS）判断还是否连通
  
• 再把节点v加入图中

若用邻接表（adjacency list），需要做V次DFS，时间复杂度为O(V∗(V+E))。（题外话：我在面试实习的时候，只想到暴力方法；面试官提示只要一次DFS就就可以找到割点，当时死活都没想出来）。

有关DFS搜索树的概念

在介绍算法之前，先介绍几个基本概念

• DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树，如图(b)所示。
  
• 树边：（在[2]中称为父子边），在搜索树中的实线所示，可理解为在DFS过程中访问未访问节点时所经过的边。
  
• 回边：（在[2]中称为返祖边、后向边），在搜索树中的虚线所示，可理解为在DFS过程中遇到已访问节点时所经过的边。

基于DFS的算法

该算法是R.Tarjan发明的。观察DFS搜索树，我们可以发现有两类节点可以成为割点：

1. 对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；
   
2. 对非叶子节点u（非根节点），若其子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与u的子树的节点不再连通；则节点u为割点。

对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。

我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点（即DFS次序号最小），那么low[u]的计算过程如下：
low[u]={min{low[u], low[v]}min{low[u], dfn[v]}(u,v)为树边(u,v)为回边且v不为u的父亲节点

下表给出图(a)对应的dfn与low数组值。

i0123456789101112vertexABCDEFGHIJKLMdfn[i]15121011138694723low[i]1115515582511

对于情况2，当(u,v)为树边且low[v] >= dfn[u]时，节点u才为割点。该式子的含义：以节点v为根的子树所能追溯到最早的祖先节点要么为v要么为u。

代码实现

void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;

//记录节点u的子树数
int children = 0;

ArcNode *p = graph[u].firstArc;
visit[u] = 1;


//初始化dfn与low
dfn[u] = low[u] = ++counter;


for(; p != NULL; p = p->next) {
int v = p->adjvex;

//节点v未被访问，则(u,v)为树边
if(!visit[v]) {
children++;
parent[v] = u;
dfs(v);


low[u] = min(low[u], low[v]);


//case (1)
if(parent[u] == NIL && children > 1) {
printf("articulation point: %d\n", u);
}


//case (2)
if(parent[u] != NIL && low[v] >= dfn[u]) {
printf("articulation point: %d\n", u);
}
}


//节点v已访问，则(u,v)为回边
else if(v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}

采用邻接表存储图，该算法的时间复杂度应与DFS相同，为O(V+E)。

另一种理解：

DFS遍历一个图的所有顶点时，按访问顺序依次标号为1到n，称之为DFS数。顶点v的DFS数记作D(v)。并得到一棵DFS树（黑色边），称DFS树的边为树边（tree edge），其余的边（红色边）称为回头边（back edge）。如下图，图的边都按搜索过程中向外的方向定向，得到一个有向图。树边都是从DFS数小的顶点指向大的，回头边都是从DFS数大的顶点指向小的。

 

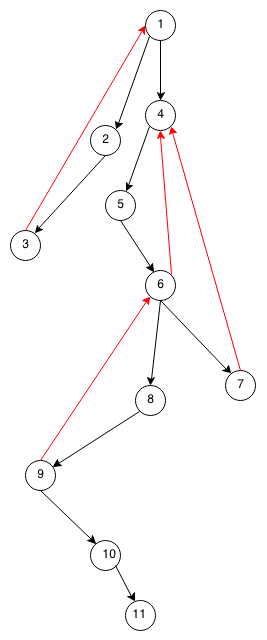
根据上面由深度优先搜索得到的有向图中，可定义每个顶点的低位数（lowpoint）：从该顶点出发，只用最多一条回头边，沿有向边能走到的顶点中DFS数最小值。顶点v的低位数记为L(v)。

低位数取值有两种情况：一是没用上回头边，则能走到的DFS数最小的的顶点就是该点自身，对应的路是一个顶点构成的平凡的路。此时L(v)=D(v)。二是用了回头边，则一定是最后一条边是回头边，走到一个DFS数更小的顶点。此时L(v)<=D(v)。

所以，一般地，总有L(v)<=D(v)。

有了这两个参数，就可以确定割点了：对根节点，即DFS数为1的顶点，其为割点当且仅当在DFS树中有两个或以上子节点；其余所有非根节点v是割点的充分必要条件是：v存在一个子节点u（在DFS树中的子节点）满足u的低位数大于等于v的DFS数，即L(u)>=D(v)。

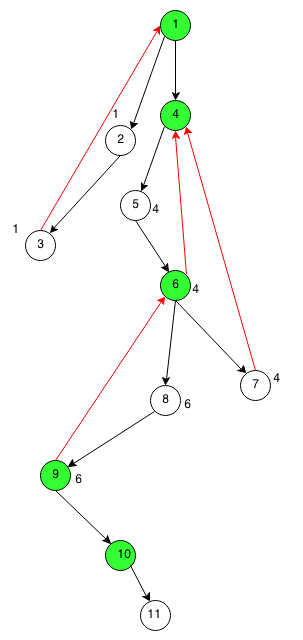
下图标出的顶点的低位数（圈外数字，没标圈外数字的顶点低位数和DFS数相等），绿色顶点为割点。

注：若用 DFS的深度（depth）来替代上面算法中的DFS数，并用深度来计算低位数，则算法一样能有效地找出割点。

求割点 割边的代码实现：

//求割点

#include <vector>
bool cut[nMax];   //cut[x] = ture 代表x 为割点
int dfn[nMax], low[nMax];  //dfn[x] x是当前层次，low[x] x是能到得的最低层次
//这两个或许有点摸不着头脑，不过没关系，
//查下tarjan 自己画画差不多就能理解,tarjan只是个帅哥名字，没那么可怕
vector<int> adj[nMax];
int rt, rt_num; //起始节点和访问此结点的次数，如果大于一则rt也为割点
//用于判断起始结点是否也是割点
/**
    nMax为点的个数;
    rt选任意一点;
    rt_num = 0;
*/

void addEdge(int u, int v) {
    adj[u].push_back(v);
    adj[v].push_back(u);
}

void findcut(int dep, int u) {
    dfn[u] = low[u] = dep;
    for (int i=0; i<adj[u].size(); i++) {
        int v = adj[u][i];
        if (!dfn[v]) {
            findcut(dep+1, v);
            if (u == rt)
                rt_num++;
            else {
                low[u] = min(low[u], low[v]);
                if (low[v] >= dfn[u])
                    cut[u] = true;  //如果满足这个条件则u 为割点

            }
        }
        else
            low[u] = min(low[u], dfn[v]);
    }
}

int main() {

    //初始化
    /**
        dfn = 0, cut = 0, rt_num = 0;
        adj[i].clear(); //对边集进行清空
    */
    //建好图后调用
    findcut(1, rt); //rt 任选 1 - n
    if (rt_num > 1)
        cut[rt] = true;

    //则cut 中为 true 的即为割点
    return 0;
}

//求割边
void findcut(int dep, int u, int f) {
    dfn[u] = low[u] = dep;
    for (int i=0; i<adj[u].size(); i++) {
        int v = adj[u][i];
        if (!dfn[v]) {
            findcut(dep+1, v, u);

            low[u] = min(low[u], low[v]);
            if (low[v] > dfn[u])
                cut[u][v] = true;  //如果满足这个条件则adj(u, v)为割边

        }
        else if (f != v)
            low[u] = min(low[u], dfn[v]);
    }
}

//调用即可
    findcut(1, 1, 0);

/**
    还是那句话，模板都会用，关键在转换
*/