有关赌徒必胜方法

今天看到一道笔试题。如下：

某福彩机构推出了一款简单的猜谜游戏：游戏玩家只需交纳n元，赌红或者黑。如果开奖结果与游戏玩家所赌的颜色相同，则玩家除得到交纳的n元赌资外，还可以获得n元作为奖励；否则该玩家失去交纳的n元赌资。为了游戏公平，开奖是红或者黑的概率均为1/2。某游戏玩家想出了一个玩法：开始出100元参与赌博，然后按照如下规则进行游戏，如果输掉，并且赌资充足，就把已经输了的总钱数翻倍作为赌资进行赌博；否则，就停止该游戏。假定该机构赌资无限，而玩家的赌资比较有限，以下关于该玩家退出游戏时的情形的评论中合理的是：

A. 该玩家的策略可以保证游戏结束时赢钱数的期望为正数

B. 该福彩机构长期会赔钱

C. 该玩家会有一定概率在游戏结束时输钱，但输得不多

D. 该玩家赢的可能性比输的可能性大

先说答案，答案为A。A:因为题目中说，玩家赌资比较有限，并且赢了之后，就结束游戏，所以按照这种策略，赢钱的期望还是很大的，为正数。

B.机构的其他玩家赌资，以及策略未必跟这个玩家相同。

C.如果玩家连续输的话，会把所有的钱都输掉，所以输的很多！！！

D.错，单次的话，输赢可能性都是1/2。

要更深入地理解此道题目，先看matrix67的一篇博文：

--------------------------------------

用数学解赌博问题不稀奇，用赌博解数学问题才牛B

    有一个经典的概率问题：平均需要抛掷多少次硬币，才会首次出现连续的 n 个正面？它的答案是 2^(n+1) – 2 。取 n=2 的话，我们就有这样的结论：平均要抛掷 6 次硬币，才能得到两个连续的正面。或许这个期望次数比你想象中的要多吧。我们不妨试着来验证一下这一结果。由简单的递推可得，所有 1 都不相邻的 k 位 01 串有 Fk+2 个，其中 Fi 表示 Fibonacci 数列中的第 i 项。而“抛掷第 k 次才出现连续两个正面”的意思就是， k 位 01 串的末三位是 011 ，并且前面 k – 3 位中的数字 1 都不相邻。因此，在所有 2^k 个 k 位 01 串中，只有 Fk-1 个是满足要求的。因此，我们要求的期望值就等于 ∑ (k=2..∞) k * Fk-1 / 2^k 。这个无穷级数就等于 6 。我怎么算的呢？我用 Mathematica 算的。

      

 
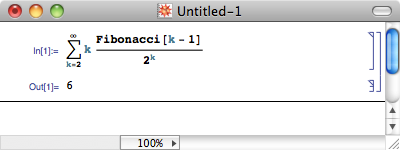
    显然，当 n 更大的时候，期望值的计算更加复杂。而简单美妙的结论让我们不由得开始思考，这个问题有没有什么可以避免计算的巧妙思路？万万没有想到的是，在赌博问题的研究中，概率论帮了不少大忙；而这一回，该轮到赌博问题反过来立功了。

    设想有这么一家赌场，赌场里只有一个游戏：猜正反。游戏规则很简单，玩家下注 x 元钱，赌正面或者反面；然后庄家抛出硬币，如果玩家猜错了他就会输掉这 x 元，如果玩家猜对了他将得到 2x 元的回报（也就是净赚 x 元）。
    让我们假设每一回合开始之前，都会有一个新的玩家加入游戏，与仍然在场的玩家们一同赌博。每个玩家最初都只有 1 元钱，并且他们的策略也都是相同的：每回都把当前身上的所有钱都押在正面上。运气好的话，从加入游戏开始，庄家抛掷出来的硬币一直是正面，这个玩家就会一直赢钱；如果连续 n 次硬币都是正面朝上，他将会赢得 2^n 元钱。这个 2^n 就是赌场老板的心理承受极限——一旦有人赢到了 2^n 元钱，赌场老板便会下令停止游戏，关闭赌场。让我们来看看，在这场游戏中存在哪些有趣的结论。

    首先，连续 n 次正面朝上的概率虽然很小，但确实是有可能发生的，因此总有一个时候赌场将被关闭。赌场关闭之时，唯一赚到钱的人就是赌场关闭前最后进来的那 n 个人。每个人都只花费了 1 元钱，但他们却赢得了不同数量的钱。其中，最后进来的人赢回了 2 元，倒数第二进来的人赢回了 4 元，倒数第 n 进来的人则赢得了 2^n 元（他就是赌场关闭的原因），他们一共赚取了 2 + 4 + 8 + … + 2^n = 2^(n+1) – 2 元。其余所有人初始时的 1 元钱都打了水漂，因为没有人挺过了倒数第 n + 1 轮游戏。
    另外，由于这个游戏是一个完全公平的游戏，因此赌场的盈亏应该是平衡的。换句话说，有多少钱流出了赌场，就该有多少的钱流进赌场。既然赌场的钱最终被赢走了 2^(n+1) – 2 元，因此赌场的期望收入也就是 2^(n+1) – 2 元。而赌场收入的唯一来源是每人 1 元的初始赌金，这就表明游戏者的期望数量是 2^(n+1) – 2 个。换句话说，游戏平均进行了 2^(n+1) – 2 次。再换句话说，平均抛掷 2^(n+1) – 2 次硬币才会出现 n 连正的情况。

-----------

之后再看知乎上的一个回答：

原问题：

赌徒「必胜方法」 对不对？修改

有一个广泛流传于赌徒中的“必胜方法”，是关于赌徒悖论极好的说明:

一个赌场设有“猜大小”的赌局，玩家下注后猜“大”或者猜“小”，如果输了，则失去赌注，如果赢的话，则获得本金以及0.9倍的利润。 “必胜法”是这么玩的：
（1）押100猜“大”；
（2）如果赢的话，返回（1）继续；
（3）如果输的话则将赌注翻倍后继续猜“大”，因为不可能连续出现“大”，总会有获胜的时候，而且由于赌注一直是翻倍，只要赢一次，就会把所有输掉的钱赢回；
（4）只要赢了，就继续返回（1）。

回答：

题目描述的「必胜方法」本身是有问题的：

「必胜方法」里面最重要的一点，是要保证「只要有一次胜利，就可以收回之前输掉的所有赌注，外加利润 X 元」。

题目里，赢的时候只有 0.9 倍利润。如果只是翻倍下注，连续多次失败后的胜利会收不回之前输掉的赌注。

正确的「必胜方法」应当将步骤（3）修改为：

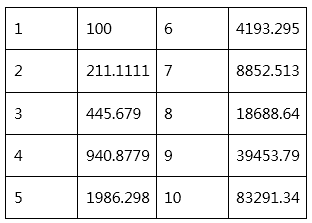
如果输，则下次押注为 ( 连续输掉的资金 + 利润 X 元 ) / 0.9

假设利润为 90 元， 前十次下注应为此数列：

但这要算起来很麻烦，下面姑且把条件改为「如果赢，则获取本金 * 2」来计算。

不妨先赌一把试试：
每局押 100 元，发哥带着 50000 的本金入场。
假设每局玩 1 分钟，那么每小时 60 次，每天可以玩 360 次。
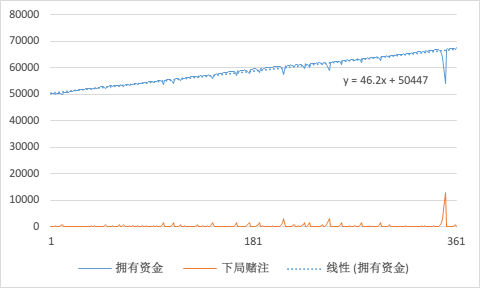
那么第一天过去呢，看下发哥战绩如何呢？


看起来战绩不错呢：

天亮时，手里的钱已经有 67500 了，日入一万七，发哥觉得自己似乎找到了生命的真谛，一张丑脸上不禁泛起了微笑。

哦对了，为了让我们的实验更加严谨，要先商量好，如果万一连续赌输，资金不够支持下一次赌注的时候，采取什么策略。

这里采取的策略：
下次赌注为全部余下资金，如果赌赢，那么回到（1）押100猜「大」；
采取这种策略的原因是……这样编程比较方便。

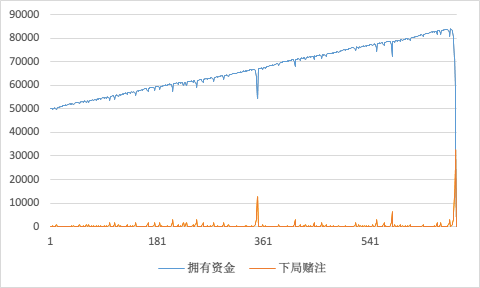
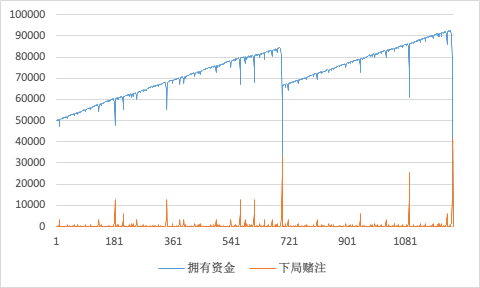
转眼又是一天过去了，来看下发哥今天战绩如何吧？

咦，发哥你怎么不到天亮就回来了？
什么，输光光？！
到底发生了什么事？！


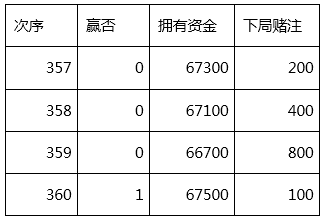
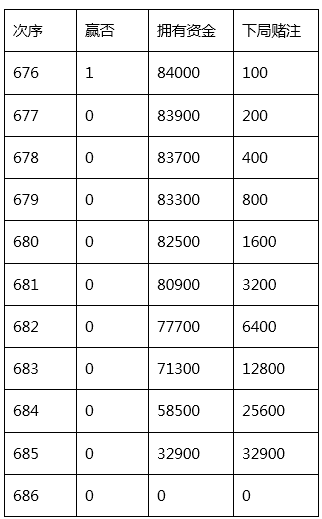
可以看到，从第 676 次时，发哥连续遇到了 10 次「小」， 好不容易积攒起来的 8 万财富毁于一旦。

此处应该有掌声。

痛定思痛，在排除了「赌场出老千」的因素以后，发哥总归还是不太甘心的……毕竟连续掷出 10 个「小」实在是很少见。

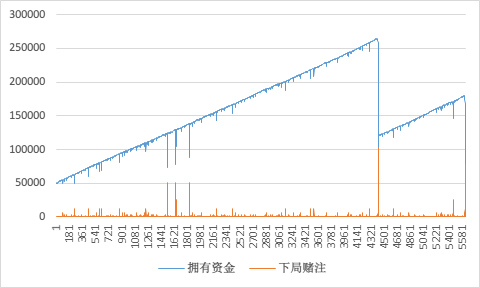
由于本宇宙的资金已经耗尽，那么我们就派出平行宇宙的发哥再战一百回合吧！
…………死于第 4 天。

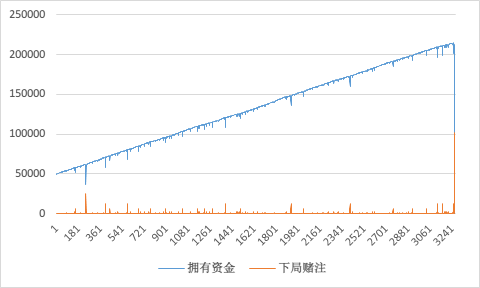
不甘心，再来！
死于第 15 天。

再来！
第 9 天。

再来！

不来了，直接派出 100 个发哥荒野求生吧。

20 年以后， 100 个中，能坚持自己梦想的有几人呢？

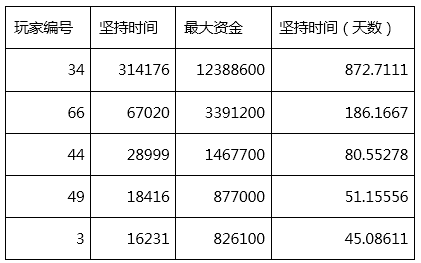
结果出来了，先给众看官展示一下个人财富 Top 5 吧：

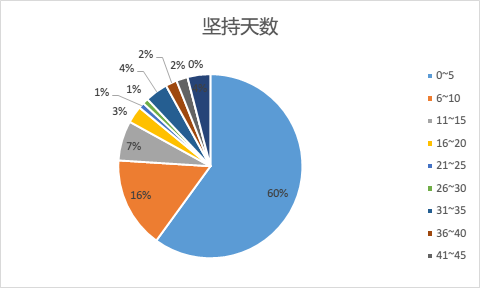
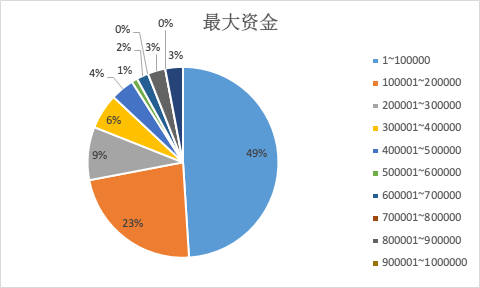
然后放出大饼图：



如你所见，60% 的赌徒会在 5 天左右输光光，而半个月过后，还在继续的赌徒只剩 17% ，如果你足够努力，闯入三甲，那你账面上最多时会超过 100 万资金。

前三甲以外的朋友们，在 50 天左右全部申请破产。

另外，不得不提一下第一名这种不世出的天才，竟然坚持了 800 多天，巅峰期达到上千万，疯狂玷污实验数据……

咳咳，所以说，实验结论就是，在统计数据明显不够充足的情况下（=_=），97% 的玩家在 50 天左右就输光，但与此同时，想依靠此路挣个上千万也不是没有可能的。

另外，别忘了这是建立在输赢五五开、没有人出千、以及赌资不设上下限的情况下的。

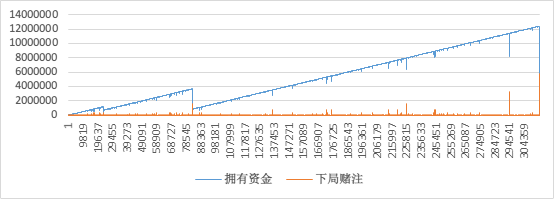
SHOW TIME! 赌博届的天才少年：

看看人家的纵坐标刻度，200 万一刻，啧啧啧。

实验做完了，下面开始分析：

发哥初始资金带了 50000，每次押注 100，为了方便一点我们假设他带了51200 入场。

这样，在 51200 ~ 102300 这个区间，如果连续掷 9 次「小」，就还能剩下 100 ~ 51100 。也就是说，虽然连续 10 次「小」才会输光，但是连续 9 次「小」，就已经让这个策略无法继续进行。

过了这个节点，能承受的次数加 1 。

根据之前的拟合方程，大概需要 (102300 – 51200) / 46.2 = 1106.06 次赌博（不精确，这里近似使用）。

然后，我们再算一下，平均需要掷多少次骰子，才会出现一个连续 9 个「小」？

一般来说，这里的思维是根据递推来算，但是我今天突然撞见了 Matrix67: My Blog 大神的优秀解法：

设想有这么一家赌场，赌场里只有一个游戏：猜正反。游戏规则很简单，玩家下注 x 元钱，赌正面或者反面；然后庄家抛出硬币，如果玩家猜错了他就会输掉这 x 元，如果玩家猜对了他将得到 2x 元的回报（也就是净赚 x 元）。
让我们假设每一回合开始之前，都会有一个新的玩家加入游戏，与仍然在场的玩家们一同赌博。每个玩家最初都只有 1 元钱，并且他们的策略也都是相同的：每回都把当前身上的所有钱都押在正面上。运气好的话，从加入游戏开始，庄家抛掷出来的硬币一直是正面，这个玩家就会一直赢钱；如果连续 n 次硬币都是正面朝上，他将会赢得 2^n 元钱。这个 2^n 就是赌场老板的心理承受极限——一旦有人赢到了 2^n 元钱，赌场老板便会下令停止游戏，关闭赌场。让我们来看看，在这场游戏中存在哪些有趣的结论。
首先，连续 n 次正面朝上的概率虽然很小，但确实是有可能发生的，因此总有一个时候赌场将被关闭。赌场关闭之时，唯一赚到钱的人就是赌场关闭前最后进来的那 n 个人。每个人都只花费了 1 元钱，但他们却赢得了不同数量的钱。其中，最后进来的人赢回了 2 元，倒数第二进来的人赢回了 4 元，倒数第 n 进来的人则赢得了 2^n 元（他就是赌场关闭的原因），他们一共赚取了 2 + 4 + 8 + … + 2^n = 2^(n+1) - 2 元。其余所有人初始时的 1 元钱都打了水漂，因为没有人挺过了倒数第 n + 1 轮游戏。
另外，由于这个游戏是一个完全公平的游戏，因此赌场的盈亏应该是平衡的。换句话说，有多少钱流出了赌场，就该有多少的钱流进赌场。既然赌场的钱最终被赢走了 2^(n+1) - 2 元，因此赌场的期望收入也就是 2^(n+1) - 2 元。而赌场收入的唯一来源是每人 1 元的初始赌金，这就表明游戏者的期望数量是 2^(n+1) - 2 个。换句话说，游戏平均进行了 2^(n+1) - 2 次。再换句话说，平均抛掷 2^(n+1) - 2 次硬币才会出现 n 连正的情况。

所以，出现 n 连「小」的时候，平均掷骰子的次数的期望为： 2 ^ ( n + 1 ) – 2 次。
连续掷 9 次都是「小」，平均需要掷 2 ^ ( 9 + 1 ) – 2 = 1022 次。

而根据之前的数据，资金能成长到可以承受连续 10 次「小」，需要约 1106.06 次。
也就是说，在黎明到来之前，通常已经出现了生命不可承受之重。

即使你熬过了这个阶段，也无需骄傲，从 10 ~ 11 次的成长需要更久的时间，也带来了足够的几率将你打到。

此种策略，之所以看上去赢面非常大，实际上是因为一个非常容易忽略的原因，就是：
在这种条件下，一旦输，就是全部输光。

换言之，这个游戏从「赢，得 100 ；输，失 100」，变为了「赢，得 100 ；输，失 50000」。

赢面当然会变大！



最后啰嗦一句：
珍惜生命，远离赌博。