斯特林数
来源:互联网 发布:公需科目大数据是什么 编辑:程序博客网 时间:2024/05/10 22:57
斯特林数出现在许多组合枚举问题中. 对第一类斯特林数 StirlingS1[n,m], 给出恰包含 m 个圈的 n 个元素 的排列数目. 斯特林数满足母函数关系 . 注意某些 的定义与 Mathematica 中的不同,差别在于因子 . 第二类斯特林数 StirlingS2[n,m]给出把 n 个可区分小球分配到m个不可区分的的盒子,且盒子没有空盒子的方法的数量. 它们满足关系 . 划分函数 PartitionsP[n]给出把整数 n 写为正整数的和,不考虑顺序的方法的数目. PartitionsQ[n]给出把整数 n 写为正整数的和,并且和中的整数是互不相同的 写法的数目设S(p,k)是斯特林数S(p,k)的一个组合学解释是:将p个物体划分成k个非空的不可辨别的(可以理解为盒子没有编号)集合的方法数。S(p,k)的递推公式是: S(p,k) = k*S(p-1,k) + S(p-1,k-1) ,1<= k <=p-1边界条件:S(p,p) = 1 ,p>=0S(p,0) = 0 ,p>=1递推关系的说明:考虑第p个物品,p可以单独构成一个非空集合,此时前p-1个物品构成k-1个非空的不可辨别的集合,方法数为S(p-1,k-1);也可以前p-1种物品构成k个非空的不可辨别的集合,第p个物品放入任意一个中,这样有k*S(p-1,k)种方法。第一类斯特林数和第二类斯特林数有相同的初始条件,但递推关系不同。引用Brualdi《组合数学》里的一段注释“对于熟悉线性代数的读者,解释如下:具有(比如)实系数,最多为p次的那些各项式形成一个p+1维的向量空间。组1,n,n^2,...。n^p和组A(n, 0),A(n,1),A(n,2),... ,A(n,p)都是该空间的基。第一类Stirling数和第二类Stirling数告诉我们如何用其中的一组基表示另一组基。斯特灵数[编辑]
维基百科,自由的百科全书在组合数学,Stirling数可指两类数,都是由18世纪数学家James Stirling提出的。
第一类[编辑]
第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有![s(n,k) , \left[\begin{matrix} n \\ k \end{matrix}\right]](http://upload.wikimedia.org/math/8/4/9/8494c8de074f7e71c7fbb634d3f83fd6.png) 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。
- 给定
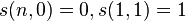 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。



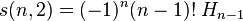
![s(n,3) = \frac{1}{2} (-1)^{n-1} (n-1)! [ (H_{n-1})^2 - H_{n-1}^{(2)} ]](http://upload.wikimedia.org/math/8/b/0/8b074a8e91fdb536ac2e87387cf3ff12.png)
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
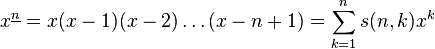
第二类[编辑]
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有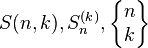 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此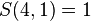 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此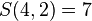 。
。
- 给定
 ,有递归关系
,有递归关系
- 递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。




 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。
两者关系[编辑]
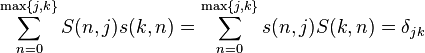
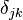 是克罗内克尔δ。
是克罗内克尔δ。
4
Posted by: spoiler in: 斯特林数的各种应用
题目:
Problem DescriptionIn many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number. InputInput consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 ≤ n ≤ 107 on each line. Output
The output contains the number of digits in the factorial of the integers appearing in the input. Sample Input21020
Sample Output719
题目分析:
第一种做法:
N!=1*2*3....*n
求位数我们一般用对一个数取对数就可以了 ,
log10(n!)=log10(1)+ log10(2) +log10(3)...+log10(n);
所以循环求和就可以了!
但是这里注意一点 结果要加1!因为这里计算出来的 log10(1)=0 !
所以结果要加上这个误差 ‘1’
第二种做法:
这就是我最近研究的斯特林数,第一类斯特林数就可以做这个!
补充一点,斯特林数能够做一切关于阶乘有关的大数运算 要深入学习!
这里给出递归公式:
log10(n!)=1.0/2*log10(2*pi*n)+n*log10(n/e)
然后我就附上代码了;
两种做法都有!
第二类做法 12345678910111213141516#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,n; cin>>cas; while(cas--){ scanf("%d",&n); ans=(int)(1.0/2.0*log(2.0*pi*n)/log(10.0)+1.0*n*log(n/e)/log(10.0)+1); printf("%d\n",ans); } return0;}第一类做法 12345678910111213141516171819#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,i,n; double sum; cin>>cas; while(cas--){ scanf("%d",&n); sum=1; for(i=1;i<=n;i++) sum+=log10(i); printf("%d\n",((int)sum)); } return0;}
- Comments(5)
HDU 3625( Examining the Rooms 斯特林数的应用 )
204
Posted by: spoiler in: 斯特林数的各种应用
题目:
就是给你N个房间,然后每个房间1把钥匙,你最初手里没有任何钥匙,要靠破门而入!这里只有第一个房间不能破门进去,其他都可以,
给你房间数N,和最多能破门的个数,让你求能全部把房间打开的概率!
题目分析:
又是是我的第一次啊!受教育了?有木有?这种题目是斯特林第一类数的应用,虽然很裸,但是很经典啊 !
首先这题其实让我们求的是给 N个元素,让我们求K个环排列的 方法数。
斯特林第一类数的第推公式:
S(N,0)=0;
S(N,N)=1;
S(0,0)=0;
S(N,K)=S(N-1,K-1)+S(N-1,K)*(N-1);
这个公式的意思是:
当前N-1个数构成K-1 个环的时候,加入第N个 ,N只能构成单环!---S(N-1,K-1)
如果N-1个数构成K个环的时候,加入第N个,N可以任意加入,N-1内的一个环里,所以是--(N-1)*S(N-1,K)
这个题目里,因为不能破坏第1个门:
所以
S(N,K)-S(N-1,K-1)才是能算构成K个环的方法数!就是去掉1自己成环的情况!
代码:
1234567891011121314151617181920212223242526272829303132333435363738394041424344#include<iostream>#include<cstdio>#include<cstring>usingnamespacestd;constintmaxn=20;long long f[25],stir[25][25];intsolve(){ inti,j; f[0]=1; for(i=1;i<=maxn;i++) f[i]=i*f[i-1]; //因为N有N!种排列顺序,这作为总数 //计算概率 for(i=1;i<=maxn;i++) stir[i][0]=0; stir[1][1]=1; for(i=1;i<=maxn;i++) for(j=1;j<=i;j++){ if(i==j) stir[i][j]=1; else stir[i][j]=stir[i-1][j-1]+(i-1)*stir[i-1][j]; } for(i=1;i<=maxn;i++) for(j=1;j<=maxn;j++) if(stir[i][j]<0) stir[i][j]=-stir[i][j]; return0;}intmain(){ intcas,n,i,k; long long sum; solve(); scanf("%d",&cas); while(cas--){ scanf("%d %d",&n,&k); sum=0; for(i=1;i<=k;i++) sum+=stir[n][i]-stir[n-1][i-1]; printf("%.4lf\n",1.0*sum/f[n]);//因为写成printf("%.4lf\n",(double)sum/f[n]); //run time error! 下次一定记好了! } return0;}
斯特灵数[编辑]
在组合数学,Stirling数可指两类数,都是由18世纪数学家James Stirling提出的。
第一类[编辑]
第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有![s(n,k) , \left[\begin{matrix} n \\ k \end{matrix}\right]](http://upload.wikimedia.org/math/8/4/9/8494c8de074f7e71c7fbb634d3f83fd6.png) 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。
- 给定
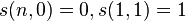 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
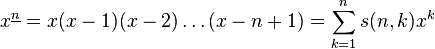
第二类[编辑]
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有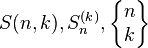 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此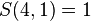 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此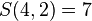 。
。
- 给定
 ,有递归关系
,有递归关系
- 递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。




 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。
两者关系[编辑]
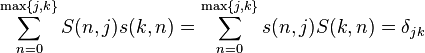
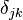 是克罗内克尔δ。
是克罗内克尔δ。
4
Posted by: spoiler in: 斯特林数的各种应用
题目:
The output contains the number of digits in the factorial of the integers appearing in the input.
21020
719
题目分析:
第一种做法:
N!=1*2*3....*n
求位数我们一般用对一个数取对数就可以了 ,
log10(n!)=log10(1)+ log10(2) +log10(3)...+log10(n);
所以循环求和就可以了!
但是这里注意一点 结果要加1!因为这里计算出来的 log10(1)=0 !
所以结果要加上这个误差 ‘1’
第二种做法:
这就是我最近研究的斯特林数,第一类斯特林数就可以做这个!
补充一点,斯特林数能够做一切关于阶乘有关的大数运算 要深入学习!
这里给出递归公式:
log10(n!)=1.0/2*log10(2*pi*n)+n*log10(n/e)
然后我就附上代码了;
两种做法都有!
#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,n; cin>>cas; while(cas--){ scanf("%d",&n); ans=(int)(1.0/2.0*log(2.0*pi*n)/log(10.0)+1.0*n*log(n/e)/log(10.0)+1); printf("%d\n",ans); } return0;}#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,i,n; double sum; cin>>cas; while(cas--){ scanf("%d",&n); sum=1; for(i=1;i<=n;i++) sum+=log10(i); printf("%d\n",((int)sum)); } return0;}
- Comments(5)
HDU 3625( Examining the Rooms 斯特林数的应用 )
204
Posted by: spoiler in: 斯特林数的各种应用
题目:
就是给你N个房间,然后每个房间1把钥匙,你最初手里没有任何钥匙,要靠破门而入!这里只有第一个房间不能破门进去,其他都可以,
给你房间数N,和最多能破门的个数,让你求能全部把房间打开的概率!
题目分析:
又是是我的第一次啊!受教育了?有木有?这种题目是斯特林第一类数的应用,虽然很裸,但是很经典啊 !
首先这题其实让我们求的是给 N个元素,让我们求K个环排列的 方法数。
斯特林第一类数的第推公式:
S(N,0)=0;
S(N,N)=1;
S(0,0)=0;
S(N,K)=S(N-1,K-1)+S(N-1,K)*(N-1);
这个公式的意思是:
当前N-1个数构成K-1 个环的时候,加入第N个 ,N只能构成单环!---S(N-1,K-1)
如果N-1个数构成K个环的时候,加入第N个,N可以任意加入,N-1内的一个环里,所以是--(N-1)*S(N-1,K)
这个题目里,因为不能破坏第1个门:
所以
S(N,K)-S(N-1,K-1)才是能算构成K个环的方法数!就是去掉1自己成环的情况!
代码:
#include<iostream>#include<cstdio>#include<cstring>usingnamespacestd;constintmaxn=20;long long f[25],stir[25][25];intsolve(){ inti,j; f[0]=1; for(i=1;i<=maxn;i++) f[i]=i*f[i-1]; //因为N有N!种排列顺序,这作为总数 //计算概率 for(i=1;i<=maxn;i++) stir[i][0]=0; stir[1][1]=1; for(i=1;i<=maxn;i++) for(j=1;j<=i;j++){ if(i==j) stir[i][j]=1; else stir[i][j]=stir[i-1][j-1]+(i-1)*stir[i-1][j]; } for(i=1;i<=maxn;i++) for(j=1;j<=maxn;j++) if(stir[i][j]<0) stir[i][j]=-stir[i][j]; return0;}intmain(){ intcas,n,i,k; long long sum; solve(); scanf("%d",&cas); while(cas--){ scanf("%d %d",&n,&k); sum=0; for(i=1;i<=k;i++) sum+=stir[n][i]-stir[n-1][i-1]; printf("%.4lf\n",1.0*sum/f[n]);//因为写成printf("%.4lf\n",(double)sum/f[n]); //run time error! 下次一定记好了! } return0;}
4
Posted by: spoiler in: 斯特林数的各种应用
题目:
The output contains the number of digits in the factorial of the integers appearing in the input.
21020
719
题目分析:
第一种做法:
N!=1*2*3....*n
求位数我们一般用对一个数取对数就可以了 ,
log10(n!)=log10(1)+ log10(2) +log10(3)...+log10(n);
所以循环求和就可以了!
但是这里注意一点 结果要加1!因为这里计算出来的 log10(1)=0 !
所以结果要加上这个误差 ‘1’
第二种做法:
这就是我最近研究的斯特林数,第一类斯特林数就可以做这个!
补充一点,斯特林数能够做一切关于阶乘有关的大数运算 要深入学习!
这里给出递归公式:
log10(n!)=1.0/2*log10(2*pi*n)+n*log10(n/e)
然后我就附上代码了;
两种做法都有!
#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,n; cin>>cas; while(cas--){ scanf("%d",&n); ans=(int)(1.0/2.0*log(2.0*pi*n)/log(10.0)+1.0*n*log(n/e)/log(10.0)+1); printf("%d\n",ans); } return0;}#include<iostream>#include<cmath>#include<cstdio>#define e 2.7182818284590452354#define pi acos(-1)usingnamespacestd;intmain(){ intcas,ans,i,n; double sum; cin>>cas; while(cas--){ scanf("%d",&n); sum=1; for(i=1;i<=n;i++) sum+=log10(i); printf("%d\n",((int)sum)); } return0;}
- Comments(5)
HDU 3625( Examining the Rooms 斯特林数的应用 )
204
Posted by: spoiler in: 斯特林数的各种应用
题目:
就是给你N个房间,然后每个房间1把钥匙,你最初手里没有任何钥匙,要靠破门而入!这里只有第一个房间不能破门进去,其他都可以,
给你房间数N,和最多能破门的个数,让你求能全部把房间打开的概率!
题目分析:
又是是我的第一次啊!受教育了?有木有?这种题目是斯特林第一类数的应用,虽然很裸,但是很经典啊 !
首先这题其实让我们求的是给 N个元素,让我们求K个环排列的 方法数。
斯特林第一类数的第推公式:
S(N,0)=0;
S(N,N)=1;
S(0,0)=0;
S(N,K)=S(N-1,K-1)+S(N-1,K)*(N-1);
这个公式的意思是:
当前N-1个数构成K-1 个环的时候,加入第N个 ,N只能构成单环!---S(N-1,K-1)
如果N-1个数构成K个环的时候,加入第N个,N可以任意加入,N-1内的一个环里,所以是--(N-1)*S(N-1,K)
这个题目里,因为不能破坏第1个门:
所以
S(N,K)-S(N-1,K-1)才是能算构成K个环的方法数!就是去掉1自己成环的情况!
代码:
#include<iostream>#include<cstdio>#include<cstring>usingnamespacestd;constintmaxn=20;long long f[25],stir[25][25];intsolve(){ inti,j; f[0]=1; for(i=1;i<=maxn;i++) f[i]=i*f[i-1]; //因为N有N!种排列顺序,这作为总数 //计算概率 for(i=1;i<=maxn;i++) stir[i][0]=0; stir[1][1]=1; for(i=1;i<=maxn;i++) for(j=1;j<=i;j++){ if(i==j) stir[i][j]=1; else stir[i][j]=stir[i-1][j-1]+(i-1)*stir[i-1][j]; } for(i=1;i<=maxn;i++) for(j=1;j<=maxn;j++) if(stir[i][j]<0) stir[i][j]=-stir[i][j]; return0;}intmain(){ intcas,n,i,k; long long sum; solve(); scanf("%d",&cas); while(cas--){ scanf("%d %d",&n,&k); sum=0; for(i=1;i<=k;i++) sum+=stir[n][i]-stir[n-1][i-1]; printf("%.4lf\n",1.0*sum/f[n]);//因为写成printf("%.4lf\n",(double)sum/f[n]); //run time error! 下次一定记好了! } return0;}
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数
- 斯特林数 [Stirling Numbers]
- HDU4372(第一类斯特林数)
- HDU4372(第一类斯特林数)
- HDU 1018(斯特林数)
- 斯特林数 - 递推
- 斯特林数 组合数
- 斯特林数的研究
- 斯特林数 HDU 3625
- 第一类斯特林数 hdu4372
- shader forge初级篇|减法与除法
- [转] ubuntu下解压缩文件 .tar.gz;.tar;.bz2;.tar.bz2;.bz;.tar.bz;.zip
- hdu5670Machine
- 编程之美之找到符合条件的数
- SQL语句中的group by 和 order by
- 斯特林数
- arm的一些常用概念
- 周易六十四卦——贲卦
- ubuntu 下rar解压工具安装方法 ; .tar ; .gz ; .tar.gz 和 .tgz ; .tar.bz2 ; .bz各种解压命令
- LeetCode *** 322. Coin Change
- 深度学习参考文献及资料【持续更新】
- 1008
- POJ 1009
- 1010



