1-行列式初步

来源：互联网发布：linux local命令编辑：程序博客网时间：2024/05/16 14:00

1-行列式基础

背景

D = ∣ ∣ ∣ ∣ a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 ∣ ∣ ∣ ∣

行列式在实际工程运用中具有重大的作用，　但是对于行列式的本质意义，却有好多的解释。可以参照行列式的本质的话题。

直接借用MIT教授讲解行列式的说法：

行列式是 R^n 维空间下n维空间几何的体积。

比如在三维矩阵中：行列式的值是一个六面体的体积。

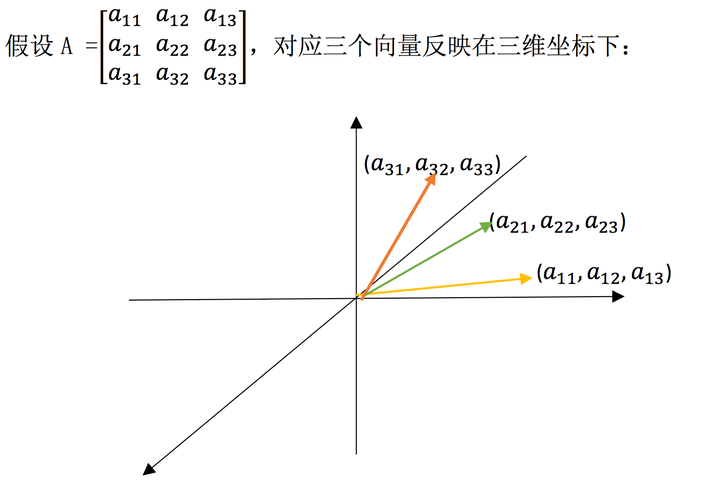
这三个向量张成了一个平行六面体，而 A 的行列式的绝对值即为其体积。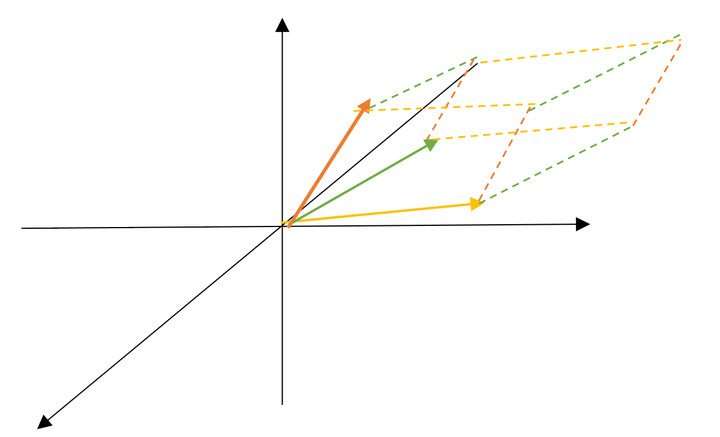

行列式的值有正负，所以该六面体的体积即为行列式的绝对值。而正负号的作用是告诉我们这个立体是左手系的还是右手系的。因为当我们调换这个立体的两条边之后，我们得到的会是不同系下的立体，其体积不会变，但是旋转顺序变了。

1. n阶行列式的计算方式

　预备知识:

逆序数:在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。一个排列中所有逆序总数叫做这个排列的逆序数。也就是说，对于n个不同的元素，先规定各元素之间有一个标准次序（例如n个不同的自然数，可规定从小到大为标准次序），于是在这n个元素的任一排列中，当某两个元素的先后次序与标准次序不同时，就说有1个逆序。一个排列中所有逆序总数叫做这个排列的逆序数。

排列中的值唯一，一个排列中的任意两个元素对换，排列改变奇偶性

-> 如果两个元素相邻，如a,b,c....i,j,...n. 如果　i,j 交换，则i,j 序列的前后的所有值的逆序数都不会发生变化，　　改变的只有i,j两个的逆序数，而这两个中的较大的值的逆序数不会发生改变，之后小值的逆序数增或者减一。  　导致整个逆序数增或者减一。   　　　　　　　　　　　　　==> 所以一组排序中的相邻两个元素交换值，逆序数增或者减一(改变奇偶性).-> 如果两个元素不相邻，假设　i,j 之间相隔m个数据，则可以看成，首先j与中间m个数据以此交换　　(需要移动到i前面同时不改变其他数据的排序)。然后m需要与这m+1个数据发生交换(移动到原先i的位置同时保证其他数据顺序)。  　　　　　　　　　　　　　 ==> 则中间移动经过　2m+1 次。-> So

方法一(通用公式):
　　
$D = \sum A n n (- 1) t a 1 p 1 a 2 p 2 . . . . a n p n$

说明:

- 对于 n 阶行列式, 总共有 n! 个子项相加。- t 为　P1P2,...Pn 的逆序数。

方法二(代数余子式方式):

取任一行i,则有公式 :

D = \sum j = i n a i j A i j

说明:

A i j = (- 1) i + j - 2 M i j

2. 行列式性质:

1.行列式与它的转置行列式相等

借助公式：

D = \sum A n n (- 1) t a 1 p 1 a 2 p 2 . . . . a n p n

对于转置事件，公式可以改写:

D = \sum A n n (- 1) t a p 1 1 * a p 2 2 * . . . . * a p n n

(针对于原 D), 元素与逆序数不会发生影响.

2.对换行列式的两行(列)，行列式变号

借助公式：

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * a i p i * a j p j * . . . * a n p n

对于交换行，公式可以改写:

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . . * a j p j * a i p i * . . . * a n p n

,由此可以看出发生了两个行排序的替换，则t的奇偶性发生改变。造成行列式变号。

行列式两行(列)相等或者成比例，则行列式为0 (D=-D).
- 3.行列式的某一行(列)的所有元素乘数k，等于用k乘以此行列式

借助公式：

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * a i p i * . . . * a n p n

对于第i行(列)乘以数k,则意味着

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * k a i p i * . . . * a n p n

.
=>

D = k \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * a i p i * . . . * a n p n

4.若行列式的某一行(列)的所有元素都是两数之和，则可以分解乘两个行列式之和

借助公式：

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * a i p i * . . . * a n p n

如果

a i p i

为　

x i + y i

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * (x i + y i) * . . . * a n p n

分解因式方式(因为对于每一个乘积元中都有特定的

x i + y i

)　=>

D = \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * x i * . . . * a n p n + \sum A n n (- 1) t a 1 p 1 * a 2 p 2 * . . . * y i * . . . * a n p n

x i

y i

对应到原来的

a i p i

,则:

D = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . a i 1 . . . a n 1 a 12 a i 2 a n 2 . . . . . . . . . a 1 n a i n a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . x 1 . . . a n 1 a 12 x 2 a n 2 . . . . . . . . . a 1 n x n a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . y 1 . . . a n 1 a 12 y 2 a n 2 . . . . . . . . . a 1 n y n a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣

5.行列式的某一行(列)的个元素乘同一个数然后加到另一行(列)的对应元素上，行列式的值不变

D = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . a i 1 . . . k a i 1 + a j 1 . . . a n 1 a 12 a i 2 k a i 2 + a j 2 a n 2 . . . . . . . . . . . . a 1 n a i n k a i n + a j n . . . a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . a i 1 . . . a j 1 . . . a n 1 a 12 a i 2 a j 2 a n 2 . . . . . . . . . . . . a 1 n a i n a j n . . . a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . a i 1 . . . k a i 1 . . . a n 1 a 12 a i 2 k a i 2 a n 2 . . . . . . . . . . . . a 1 n a i n k a i n . . . a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣

= ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 11 . . . a i 1 . . . a j 1 . . . a n 1 a 12 a i 2 a j 2 a n 2 . . . . . . . . . . . . a 1 n a i n a j n . . . a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣

6.行列式的某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和为0

利用代数余子式求和的公式逆推，这种求和意味着要求的这一行和代数余子式构成的行列式中有两行重复，所以余子式为０．

阅读全文

0 0